
C2-2011
.pdf
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Так как |
AD CDD1 , то |
AC1D явля- |
|||
ется |
углом |
между |
диагональю AC1 |
и |
|
плоскостью CDD1 , величина которого |
|||||
равна . |
|
|
|
|
|
Из |
прямоугольного |
треугольника |
|||
AC1D |
находим |
AD dsin |
и |
||
DC1 dcos . Далее из прямоугольного треугольника DCC1 получаем
CC1 
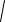 C1D2 CD2
C1D2 CD2
d
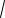 cos2 sin2 d
cos2 sin2 d
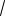 cos2 .
cos2 .
Площадь боковой поверхности призмы равна
Sбок 4 CD CC1 4d2 sin 
 cos2 .
cos2 .
Ответ: 4d2 sin 
 cos2 .
cos2 .
Пример 67. В правильной четырехугольной усеченной пирамиде стороны оснований равны a и a1 , а диагональ пирамиды – d . Определить боковую поверхность пирамиды.
Решение. Пусть в усеченной пирамиде ABCDA1B1C1D1 стороны нижнего основания равны a , верхнего – a1, а диагональ пирамиды – B1D d (см. рис. 73).
C1 |
O1 |
D1 |
|
a1 |
A1 |
||
B1 |
|
||
Ch |
d |
||
M |
|
D |
|
O |
a |
||
B N |
A |
||
|
|||
Рис. 73 |
|
||
Из вершины B1 |
проведем B1N AB и |
||
B1M BD. Так как B1N – апофема данной пирамиды, то боковая поверхность пирамиды может быть вычислена по формуле
1
Sбок 2(P P1) B1N ,
где P 4AB 4a, a P1 4A1B1 4a1 .
Отрезок B1N найдем из прямоугольного треугольника B1NM ( B1MN 90 ) . Диагонали квадратов ABCD и A1B1C1D1 ,
18.02.2011
лежащих в основаниях, равны: BD a
 2 ,
2 ,
B1D1 a1
 2 .
2 .
Диагональное сечение пирамиды – равнобочная трапеция BB1D1D . Найдем
ее высоту B1M (B1M O1O) из прямо-
угольного треугольника B1MD, т.е.
B1M 
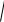 B1D2 MD2 , а MD BD BM
B1D2 MD2 , а MD BD BM
BD BD B1D1 BD B1D1 (a a1)
 2.
2.
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
Отсюда B M |
|
d2 |
(a a )2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Треугольник |
|
BMN |
|
– равнобедренный |
|||||||||||||||||||||||||
и прямоугольный ( BNM 90 ) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
BM |
(a a1) |
|
|
|
, а MN |
BM |
|
|
|
a a1 |
. |
|
|
|
|
||||||||||||||
|
2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
Теперь из треугольника B1NM находим: |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(a a ) |
2 |
|
(a a )2 |
|
||||||||||||||
B N B M2 MN2 d2 |
||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
1 |
|
|
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Подставляя найденные значения P, |
|
P1 и |
||||||||||||||||||||||||||||
|
B1N в формулу боковой поверхности пи- |
|||||||||||||||||||||||||||||
рамиды, получим ответ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Ответ: 2(a a ) |
|
d2 |
|
a2 |
|
a 2 |
|
|
3aa |
||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
4 |
|
|
|
4 |
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
метод опорных задач
● Имеет место формула
cos Sпр ,
S
где S – площадь многоугольника, лежащего в плоскости , Sпр – площадь его ортогональной проекции на плоскость .
Пример 68. Найти площадь полной поверхности правильной четырехугольной пирамиды, если ее высота равна Н, а площадь боковой грани равна площади основания.
Решение. Пусть ЕО – высота данной пирамиды ABCDE (см. рис. 74). Опустим из точки O перпендикуляр ОМ на сторону ВС квадрата ABCD и точку М соединим с вершиной E . Так как ОМ – проекция ЕМ на плоскость АВС и
41
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
OM BC, то EM BC. Значит, OME
является линейным |
углом двугранного |
|
E |
угла при ребре |
|
ВС, величину |
||
|
которого |
обо- |
|
значим |
через |
|
. |
|
A

 O
O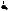









 D
D 



 M B
M B
C
Рис. 74
гласно условию имеем
Так как треугольник ВОС является проекцией боковой грани ВЕС на плоскость АВС, то со-
cos SBOC 1 .
|
|
|
|
|
|
|
|
SBEC |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
. |
||||
Тогда sin 1 |
1 |
|
|
|
|
|
|
15 |
|
и ctg |
|
|||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||||||||||||||||
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
||||||||||
|
Из треугольника ЕОМ находим |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
OM H ctg |
|
|
H |
|
|
|
и CD |
2 |
H |
|
. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
15 |
|
|
15 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Площадь основания |
|
пирамиды равна |
|||||||||||||||||||||||||||
|
4H2 |
|
|
|
|
|
|
|
|
|
|
|
16H |
2 |
|
|
|
|
|
|||||||||||
|
|
, боковой поверхности – |
|
|
|
|
|
|
|
|
, |
|
|
|
а |
|||||||||||||||
15 |
15 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
полной поверхности – |
4H |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
4H |
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 69. Стороны основания треугольной пирамиды равны 6 см, 10 см и 14 см. Каждый двугранный угол при ее основании равен 30°. Найти площадь боковой поверхности пирамиды.
Решение. Для нахождения площади сечения воспользуемся формулой
Sбок Sосн .
cos
Найдем площадь основания треугольной пирамиды, применив формулу Герона. Поскольку полупериметр треугольника в основании равен 15 см, то
Sосн 
 15 (15 6) (15 10) (15 14)
15 (15 6) (15 10) (15 14)
15
 3 (см2).
3 (см2).
18.02.2011 |
42 |
Тогда |
|
|
|
|
|
|
|
|||
|
|
Sосн |
|
|
|
|
|
|
30 (см2). |
|
Sбок |
|
15 |
|
: |
|
3 |
||||
3 |
||||||||||
cos30 |
2 |
|
||||||||
|
|
|
|
|
|
|
||||
Ответ: 30 см2.
Пример 70. В правильной усеченной четырехугольной пирамиде стороны нижнего и верхнего оснований равны соответственно a и b (a b). Найти площадь полной поверхности усеченной пирамиды, если ее боковые грани наклонены к плоскости основания под углом .
Решение. Поскольку основаниями правильной усечённой четырехугольной пирамиды являются квадраты со сторонами a и b, то сумма их площадей равна
a2 b2 . Очевидно, что ортогональная проекция боковой поверхности усеченной пирамиды на плоскость нижнего основания представляет собой квадрат со стороной a, из которого «вырезан» квадрат со стороной b. При этом стороны «вырезанного» квадрата параллельны сторонам нижнего основания пирамиды
(см. рис. 75).
b







 a
a
Рис. 75
Так как боковые грани усеченной пирамиды наклонены к плоскости основания под одинаковым углом , то площадь её боковой поверхности равна:
Sбок |
Sпр |
|
a2 b2 |
|
|
|
, |
||
cos |
|
|||
|
|
cos |
||
где Sпр – площадь проекции боковой по-
верхности на основание. Таким образом,
Sполн a2 b2 a2 b2 .
cos
Ответ: a2 b2 a2 b2 . cos
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
2.2. Площадь сечения многогранника
Свойства сечений пирамиды плоскостью, параллельной основанию.
Теорема 1. Если пересечь пирамиду плоскостью, параллельной основанию, то:
а) боковые ребра и высота пирамиды разделяются этой плоскостью на пропорциональные отрезки;
б) в сечении получится многоугольник, подобный многоугольнику, лежащему в основании;
в) площади сечения и основания будут относиться друг к другу как квадраты их расстояний от вершины пирамиды.
Теорема 2. Если две пирамиды с равными высотами пересечь плоскостями, параллельными основаниям, на одинаковом расстоянии от вершины, то площади сечений будут пропорциональны площадям оснований.
При вычислении площади сечения можно определить вид фигуры, полученной в сечении, и затем воспользоваться формулой. При этом сложную фигуру иногда разбивают на несколько простейших фигур или дополняют до простейшей.
поэтапно-вычислительный метод
Пример 71. Найдите площадь сечения правильной четырехугольной пирамиды ABCDE, проходящей через АВ и точку K
– середину ребра ЕС, если все ребра пирамиды равны 4.
Решение. Пусть |
ABK ECD KM |
(см. рис. 76). Тогда |
из AB||CD следует |
AB||ECD и KM ||AB. В сечении получаем равнобедренную трапецию АВКМ с основаниями AB 4, КМ 2 и высотой FL (F и H – середины отрезков АВ и CD соответственно, KM EH L).
Из треугольника EHF найдем медиану FL, используя формулу
FL |
2EF2 2FH 2 EH2 |
|||||||||||
|
|
|
|
|
|
|
. |
|
|
|||
4 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
2(2 |
|
|
|
|
2 |
|
|
|
|
|
||
3)2 2 42 (2 3) |
|
|
|
|||||||||
|
|
|
|
|
||||||||
FL |
|
|
|
|
|
|
|
11. |
||||
|
4 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
18.02.2011 |
|
|
|
|
|
43 |
||||||
Площадь сечения равна
SABKM 4 2 
 11 3
11 3
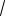 11.
11.
2
|
E |
|||
L |
K |
|||
M |
C |
|||
H |
B |
|||
F |
||||
D |
||||
|
A |
|||
|
Рис. 76 |
|||
|
Ответ: 3 |
|
. |
|
|
11 |
|||
Пример 72. В кубе ABCDA1B1C1D1 с
ребром, равным a, через точки M, P и N
на ребрах BB1 , CC1 и DD1 соответст-
венно, такие, что |
BM |
3a |
, |
CP |
2a |
и |
|||
|
|
||||||||
|
a |
|
4 |
|
3 |
|
|||
DN |
, проведена |
секущая |
плоскость. |
||||||
|
|||||||||
4 |
|
|
|
|
|
|
|
||
Найти площадь сечения.
Решение. Построим сечение куба плоскостью, проходящей через точки M, P и N. Соединим вначале точки M и P, поскольку они лежат в одной плоскости BB1C1 . Затем соединим точки P и N, так
как они лежат в одной плоскости DD1C1
(см. рис. 77).
|
B1 |
C1 |
|
A1 |
M |
L |
|
|
D1 |
P |
|
|
K |
S |
|
|
B |
||
Q |
C |
||
N |
|||
|
|||
|
|
||
A |
D |
|
|
|
Рис. 77 |
|
|
Противоположные боковые |
грани |
||
AA1D1 и BB1C1 |
в кубе параллельны. По- |
||
этому секущая плоскость, согласно свойству параллельных плоскостей (если две параллельные плоскости пересечены
www.alexlarin.narod.ru

Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
третьей, то линии пересечения параллельны) будет пересекать грань AA1D1 по прямой NQ так, что NQ|| MP.
Соединим точки M и Q, так как они лежат в одной плоскости AA1B1. Тогда MQ|| NP по тому же свойству парал-
лельных плоскостей AA1B1 и CC1D1 . Таким образом, сечение представляет собой параллелограмм MPNQ. Вычислим его площадь. Для этого найдем стороны треугольника MNP. Используя теорему Пифагора для прямоугольных треугольни-
ков MLP (ML CC1 ), NPS ( NS CC1),
MNK (KN BB1), получим:
MP |
(LC PC)2 |
ML2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a2 |
|
|
|
|
a |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
145 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
, |
||||
|
144 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|||||||||
NP |
(PC SC)2 |
NS2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
25a2 |
a |
2 |
|
|
|
|
13a |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
144 |
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|||||||||
MN |
|
(BM BK)2 KN2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
a2 |
2a |
2 |
|
|
|
|
3a |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||
Найдем площадь треугольника MNP, используя модифицированную формулу
|
|
1 |
|
|
|
|
|
|
Герона |
S |
|
4a2b2 (c2 |
a2 |
b2 )2 , |
|||
|
||||||||
|
4 |
|
|
|
|
|
||
SMNP a2 170 . Следовательно, 24
SMPNQ 2SMNP a2 
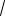 170 .
170 .
12
Ответ: a2 
 170 . 12
170 . 12
Пример 73. В единичном кубе ABCDA1B1C1D1 точка M – середина реб-
ра B1C1 , точка N лежит на диагонали
B1D, причем B1N 2ND. Найти площадь сечения куба плоскостью, проходящей через точки M, N и параллельной прямой A1C1.
Решение. Опишем схематически процесс построения сечения куба плоскостью, проходящей через точки M, N и па-
18.02.2011 |
44 |
раллельной прямой A1C1 . Для этого про-
ведем |
через |
точку |
M |
прямую ME, |
|
|
A1 |
E |
B1 |
|
|
|
|
T |
D1 |
|
|
C1 |
M |
|
|
H |
|
|
|
|
N |
K |
|
Q |
|
E1 |
||
|
A |
|||
|
F |
|
|
B |
|
|
|
M1 |
|
D |
OG |
|
C |
|
|
|
|||
|
|
L |
|
|
|
|
Рис. 78 |
|
|
ME|| A1C1 (см. рис. 78). |
|
|
||
Рассмотрим |
диагональную плоскость |
|||
B1BD, |
в которой на диагонали B1D лежит |
|||
точка N. Тогда принадлежащая сечению точка T – точка пересечения прямых ME и B1D1. В плоскости B1BD проведем прямую TN. Точка O, принадлежащая и сечению, и плоскости нижнего основания куба, – точка пересечения прямых TN и BD.
Проведем через точку O прямую GF, параллельную A1C1 . Далее, используя метод следов, построим точки H и K, принадлежащие сечению куба (шестиугольник HEMKGF). При этом шестиугольник AE1M1CGF является проекцией многоугольника HEMKGF на плоскость ABC.
Поскольку FG || A1C1 и A1C1 BD, то FG OB . Тогда OT – наклонная к плоскости ABC, прямая OB – проекция наклонной OT и OB FG . Следовательно, по теореме о трех перпендикулярах, OT FG. Значит, TOB – линейный угол двугранного угла TFGB.
Вычислим теперь косинус угла между секущей плоскостью и нижним основанием куба. Очевидно, что
BD B D |
|
, BT |
B1D1 |
|
2 |
. |
||
2 |
||||||||
|
|
|||||||
1 |
1 |
1 |
4 |
4 |
|
|||
|
|
|
|
|
||||
www.alexlarin.narod.ru

Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Далее, треугольники B1TN и DON подобны с коэффициентом подобия k 2. Следовательно,
OD B1T B1D1 
 2 , 2 8 8
2 , 2 8 8
OB BD OD 7
 2 , 8
2 , 8
OT (OB B1T)2 BB12  114 . 8
114 . 8
Откуда
cos |
OB B1T |
|
|
5 |
|
. |
|
|
|
|
|||
|
OT |
57 |
|
|
||
Вычислим, площадь шестиугольника AE1M1CGF . Площади треугольников
BM1E1 и DFG находятся довольно просто (вычислите самостоятельно!):
SBM E |
|
1 |
, SDFG |
|
1 |
. |
|
|
|
||||||
1 |
1 |
8 |
|
32 |
|
||
Тогда
27
SAE1M1CGF SABCD SBM1E1 SDFG 32 .
Таким образом,
SHEMKGF SAE1M1CGF 27
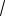 57 .
57 .
cos 160
Ответ: 27
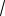 57 . 160
57 . 160
принцип разбиения и дополнения
Пример 74. Площадь боковой грани правильной шестиугольной пирамиды равна q. Найдите площадь сечения, плоскость которого параллельна боковой грани пирамиды и проходит через середину ее высоты.
Решение. Обозначим плоскость сечения через , середину высоты ОР пирамиды ABCDEFP через Т, середины отрезков ВС, OK и ЕF через K , K1 и L соответственно (см. рис. 79).
Пусть плоскость параллельна грани
РВС, |
OPK P1K1 , |
ABC QR. |
|
Тогда |
P1K1 ||PK , QR||BC, |
при этом |
|
T P1K1 , K1 QR, P1 PL. |
|
||
18.02.2011 |
|
45 |
|
Так |
как QR||AD ||EF , то пересече- |
|
ниями |
плоскости |
с треугольниками |
ADP и PEF служат соответственно отрез- |
||
ки A1D1 ||AD и |
MN ||EF (T A1D1 , |
|
M PF , N PE , P1 MN ).
Имеем A1D1 0,5AD BC, QR 1,5BC,
значит, сечением данной пирамиды плоскостью является шестиугольник QA1MND1R, составленный из двух тра-
пеций A1D1RQ и MND1A1 с общим осно-
ванием A1D1. |
|
||||
|
Пусть BC a, |
PK h, тогда |
|||
S |
PBC |
|
1 |
ah q. |
|
|
|
||||
|
2 |
|
|
||
P


 N
N
 M
M
 P1
P1 
 D1
D1
A1

 T
T
K


 C
C




 R
R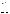


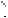 D
D



BQ




 K1 O
K1 O










 L
L 
 E
E
A F
Рис. 79
|
Найдем площадь сечения QA1MND1R. |
||||||||||||||||||||||||||||||||||
Так как K |
|
|
K |
1 |
|
OK |
|
1 |
KL и PK |
1 |
||PK , |
||||||||||||||||||||||||
1 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
1 |
|
|
|
|
|||||||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
MN |
1 |
|
EF |
|
a |
; |
PK |
|
|
3 |
|
PK |
3 |
h, |
||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
1 |
1 |
4 |
|
|
|
|
4 |
|
||||||||||||||||
|
TK |
|
|
1 |
PK |
1 |
h, |
PT |
1 |
|
h, |
|
|
|
|
||||||||||||||||||||
|
|
|
1 |
2 |
|
|
|
|
|
2 |
|
|
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
QR |
3 |
a, |
|
|
|
|
|
A D |
1 |
AD a. |
||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|||||||||||
|
Теперь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
S |
сеч |
|
A1D1 MN |
|
|
PT |
A1D1 RQ |
K T |
|||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a3a
a 4 h a 2 h 25ah 25q.
2 |
4 |
2 |
2 |
32 |
16 |
www.alexlarin.narod.ru

Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Ответ: 25q. 16
Пример 75. В основании прямой призмы ABCA1B1C1 лежит равнобедренный треугольник ABC, у которого основание BC равно 3. Боковая поверхность призмы равна 32. Найти площадь сечения призмы плоскостью, проходящей через CB1 параллельно высоте основания AD, если известно, что расстояние от точки
A до плоскости сечения равно 6 .
5
Решение. Построим сечение призмы заданной в условии плоскостью. Для этого через вершину C в плоскости ABC основания призмы проведем прямую, параллельную AD до пересечения в точке M с продолжением ребра AB за точку A (см. рис. 80). Точки M и B1 лежат в
плоскости грани AA1B1 , поэтому, проведя через них прямую, получим след E секущей плоскости на ребре AA1 . Тогда
A1
 B1
B1
Sбок h P h (2x 3).
Отсюда h |
|
|
32 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2x 3 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Выразим объем пирамиды BMB1C |
||||||||||||||||||||||||
двумя способами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1. По формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
||||||||
V |
|
|
BB |
S |
MBC |
|
|
|
h |
|
|
|
|
MC BC . |
|
|||||||||
|
|
|
2 |
|
||||||||||||||||||||
|
3 |
1 |
|
|
|
3 |
|
|
|
|
|
|
||||||||||||
Тут учтено, что треугольник |
MCB пря- |
|||||||||||||||||||||||
моугольный (MC || AD). |
|
|
|
|
|
|
|
|
|
|||||||||||||||
2. По формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
V |
1 |
BH S |
|
|
|
|
|
1 |
|
|
BH |
|
|
1 |
MC CB |
|
, |
|||||||
|
MB1C |
|
|
|
|
|
|
|||||||||||||||||
|
3 |
|
|
|
||||||||||||||||||||
|
3 |
|
1 |
|
|
|
|
|
|
1 |
|
2 |
1 |
|
|
|||||||||
где BH1 – перпендикуляр, опущенный из точки B на плоскость MB1C . Так как расстояние от точки A до этой плоскости
по условию равно 6 , а MB 2AB, то
|
|
5 |
||
BH |
|
|
12 |
. В этом случае также учтено, |
1 |
|
|||
|
5 |
|
||
что MC CC1B1 (MC CB и MC CB1)
итреугольник MCB1 – прямоугольный. Приравнивая полученные выражения
|
E C1 |
|
|
|
H1 |
|
|
|
H |
B |
|
M |
A |
||
D |
|||
|
|
C
Рис. 80
треугольник CEB1 – искомое сечение.
В треугольнике MBC отрезок AD –
средняя линия, поскольку высота AD в |
|||
равнобедренном треугольнике ABC яв- |
|||
ляется |
и |
медианой. |
Следовательно, |
MB 2AB. |
Аналогично |
в треугольнике |
|
MB1B отрезок AE – средняя линия и |
|||
MB1 2ME . |
|
|
|
Пусть |
сторона основания AB x, а |
||
высота призмы равна |
h. Тогда периметр |
основания P 2x 3 |
, боковое ребро |
призмы равно h и площадь боковой поверхности
для |
объема |
и |
учитывая, |
|
|
что |
CB1 |
||||||||||||||
|
|
|
BB2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
CB2 |
|
h2 9 , имеем |
|
|
||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
||||
|
|
h |
|
MC BC |
|
|
BH |
|
|
|
MC CB |
|
|||||||||
3 |
2 |
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
3 |
1 |
|
|
|
1 |
|
||||||||
|
4 |
|
|
|
|
25 |
h2 |
|
|||||||||||||
или h |
|
h2 |
9 . Отсюда |
h2 9 |
|||||||||||||||||
|
|
|
|||||||||||||||||||
516
иh 4, а CB1 5.
Тогда из равенства h 32 находим
2x 3
x 5 , а из треугольника ABD
2
AD 
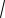 AB2 BD2
AB2 BD2 
 25 9 2. 4 4
25 9 2. 4 4
Так как точка E делит MB1 пополам, то для искомой площади сечения получаем
S |
|
SMB C |
|
1 |
MC CB |
1 |
|
|
CEB |
|
1 |
|
|
|
4 5 5. |
||
|
|
|
||||||
|
|
2 |
|
4 |
1 |
4 |
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Ответ: 5.
18.02.2011 |
46 |
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
2.3. Объем многогранника
Формулы для вычисления объема призматических тел
Объем прямой призмы
V l Sосн ,
где l – длина бокового ребра, Sосн – площадь основания.
Объем наклонной призмы
V h Sосн ,
где h – высота призмы, Sосн – площадь основания;
V l S ,
где l длина бокового ребра, S – площадь перпендикулярного ему сечения.
Объем прямоугольного параллелепипеда
V a b c,
где a,b, c – длины ребер, выходящих из одной вершины.
Формулы для вычисления объема n-угольной пирамиды
Объем произвольной пирамиды
V1 h Sосн , 3
где h – высота пирамиды, Sосн – площадь основания.
Объем произвольной усеченной пирамиды
V |
1 |
h (S |
|
|
|
S |
|
), |
|
|||||||
S S |
2 |
|
2 |
|
||||||||||||
|
|
|
|
|||||||||||||
|
|
|
3 |
1 |
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где h – высота пирамиды, S1, S2 |
– площади |
|||||||||||||||
верхнего и нижнего оснований. |
|
|
|
|
|
|||||||||||
|
||||||||||||||||
Объем правильного тетраэдра |
||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
V |
|
h Sосн |
или V |
|
|
2 |
|
, |
||||||||
3 |
12 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
где h – высота пирамиды, Sосн |
– площадь |
|||||||||||||||
основания, |
a – сторона тетраэдра. |
|
|
|
|
|||||||||||
Объем произвольного тетраэдра
V1 a b d sin , 6
где a и b – длины двух противоположных ребер тетраэдра, d и – расстояние и угол между ними соответственно.
Выделим следующие задачи данного раздела: вычисление объема многогранника и его частей, нахождение линейных и нелинейных величин многогранника по его известному объему, сравнение объемов многогранников.
поэтапно-вычислительный метод
Отметим задачи, в которых часто встречаются конфигурации с предварительным определением положения основания высоты пирамиды.
●Если все боковые ребра пирамиды равны или образуют с плоскостью основания или с высотой одинаковые углы, то основание высоты пирамиды является центром окружности, описанной около основания пирамиды.
В частности, если основанием пирамиды является прямоугольный треугольник, то высота принадлежит одной из боковых граней, содержащей гипотенузу прямоугольного треугольника, и вершина пирамиды проецируется в середину этой гипотенузы.
Если основанием пирамиды служит тупоугольный треугольник, то вершина пирамиды проецируется в точку, лежащую вне этого треугольника.
●Если все боковые грани пирамиды одинаково наклонены к плоскости основания, то основание высоты пирамиды является центром окружности, вписанной
воснование пирамиды.
Пример 76. Основание пирамиды ABCD – равнобедренный треугольник АВС с основанием AB 12 и боковой стороной 10. Найти объем пирамиды, если все боковые грани образуют с плоскостью основания двугранные углы в 45 .
Решение. Пусть CK – высота треугольника АВС (см. рис. 81), тогда из прямоугольного треугольника АСК имеем
CK 
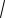 102 62
102 62 
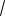 64 8.
64 8.
Площадь основания равна
1
SABC 2 12 8 48.
18.02.2011 |
47 |
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Так как все боковые грани образуют с плоскостью основания двугранные углы в 45 , то основание О высоты DO пирамиды совпадает с центром окружности, вписанной в треугольник АВС, то есть OK r, где r – радиус этой окружности.
D
 B C
B C
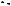
O

 K
K
A
Рис. 81
Радиус найдем по формуле
r SABC ,
p
r 48 3. 16
Так какOKD является линейным углом данного двугранного угла (докажите) и
OKD 45 ,
то из треугольника OKD имеем
OD r 3.
Объем пирамиды равен
1
VABCD 3 48 3 48.
Ответ: 48.
Пример 77. Основание пирамиды – треугольник, две стороны которого равны 1 и 2, а угол между ними равен 60 .
Каждое боковое ребро равно 
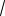 13. Найти объем пирамиды.
13. Найти объем пирамиды.
D |
|
Решение. Пусть |
|||
|
в пирамиде ABCD |
||||
|
|
основанием |
слу- |
||
|
|
жит |
треугольник |
||
|
|
ABC, |
|
причем |
|
|
|
AB 1, |
BC 2, |
||
|
B |
ABC 60 |
(см. |
||
C |
|
рис. 82). |
|
|
|
|
Так как все бо- |
||||
O |
|
||||
|
|
ковые |
ребра |
рав- |
|
|
A |
ны, то |
основание |
||
|
О высоты DO пи- |
||||
Рис. 82 |
|
||||
|
рамиды |
совпадает |
|||
|
|
с центром окруж- |
|||
ности, описанной около треугольника |
|||||
АВС, то есть |
OB R, где |
R |
– радиус |
||
этой окружности. Радиус найдем по фор- |
|||||
18.02.2011 |
|
|
|
|
48 |
муле R |
AC |
. Длину стороны АС |
|
2sin ABC |
|||
|
|
вычислим по теореме косинусов из треугольника АВС:
AC2 12 22 2 1 2 0,5 3,
AC 3. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||
|
|
|
|
|||||
Радиус окружности R |
3: |
2 |
|
|
|
|
1. |
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
Из прямоугольного треугольника BOD
найдем |
|
|
высоту |
|
|
|
|
пирамиды |
|||||||||||||||||
DO |
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Площадь осно- |
|||
13)2 12 2 |
3 |
||||||||||||||||||||||||
вания |
|
|
|
|
|
|
|
пирамиды |
|
|
равна |
||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
SABC |
1 2 |
|
|
3 |
3 |
и объем пирами- |
|||||||||||||||||||
2 |
|
2 |
|
|
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
|
|
2 |
|
|
|
||||||||||||||
ды равен VABCD |
|
|
|
|
3 |
|
|
1. |
|||||||||||||||||
|
|
|
|
3 |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
Ответ: 1.
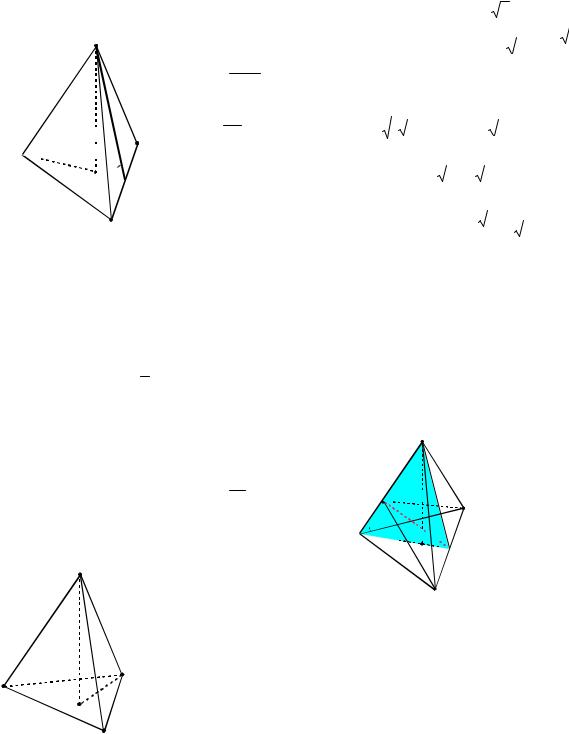
Пример 78. Найти объем правильной треугольной пирамиды, у которой боковое ребро наклонено к плоскости основания под углом ( 45 ) и удалено от противоположной стороны основания на расстояние d .
D
M

 B
B

A
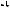


 O
O



 N
N
C
Решение. Пусть
DABC (см. рис. 83)
–данная пирамида. Так как она правильная, то основание O высоты DO
–центр треугольника ABC. Пусть точка N – середина стороны BC. Тогда DN BC и
Рис. 83 |
AN BC, а значит |
|
BC ADN . Про- |
ведем высоту MN в треугольнике ADN . |
|
Так как пирамида правильная (O AN ) и AO ON , то AND . Следовательно, треугольник ADN остроугольный и точ-
ка M AD. Соответственно |
MN – об- |
|||||
щий перпендикуляр к прямым AD и BC, |
||||||
MN d . |
|
|
|
|||
Из |
прямоугольного треугольника |
|||||
AMN |
получаем AN |
MN |
|
|
d |
. То- |
|
|
|||||
|
|
sin |
|
sin |
||
www.alexlarin.narod.ru

Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
гда сторона основания данной пирамиды равна
|
|
|
|
AN |
|
|
|
|
2d |
. |
||
|
|
|
sin60 |
|
|
|
|
|||||
|
|
|
|
|
|
3sin |
||||||
В прямоугольном треугольнике ADO |
||||||||||||
AO |
2 |
AN |
2d |
|
|
(так как O AN ), |
||||||
|
|
|
|
|
||||||||
3 |
|
|
3sin |
|||||||||
DO AO tg |
|
2d |
. |
|||||||||
|
|
|||||||||||
|
|
|
|
|
3cos |
|||||||
Находим объем пирамиды
V1 DO SABC
3
|
1 |
|
2d |
|
|
|
|
3 |
|
|
|
2d 2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
3cos |
4 |
3sin |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
2d3 |
|
|
|
|
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
9 3sin2 cos |
|
|
||||||||||||||||
|
|
|
|
|
Ответ: |
|
|
|
|
|
|
2d3 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 3sin2 |
cos |
||||||
Пример 79. Боковые ребра наклонной треугольной призмы ABCA1B1C1 равны 6 см. Сечение плоскостью, пересекающей все боковые ребра призмы и перпендикулярной им, представляет собой треугольник, стороны которого относятся как 9:10:17. Найти площадь боковой поверхности этой призмы, если известно, что объем пирамиды A1ABC равен
288 см3.
где l длина бокового ребра, S и P – площадь и периметр перпендикулярного ему сечения соответственно, Sбок пло-
щадь боковой поверхности, получим
VABCA1B1C1 AA1 SKLM или 864 6SKLM .
Отсюда SKLM 144 см2.
Найдем периметр треугольника KLM . Пусть его стороны равны 9x,10x,17x.
Тогда PKLM 36x, а полупериметр p 18x . По формуле Герона, получим
SKLM 
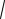 p(p 9x)(p 10x)(p 17x) 36x2 .
p(p 9x)(p 10x)(p 17x) 36x2 .
Из |
уравнения |
36x2 |
144 |
получаем |
||
x 2 |
см. |
Следовательно, |
PKLM |
72 см. |
||
Тогда S |
бок |
l P |
6 72 |
432 см2. |
||
|
|
|
|
|
|
|
Ответ: 432 см2.
введение вспомогательного отрезка
Пример 80. Все боковые грани четырехугольной пирамиды – правильные треугольники. Расстояние от центра боковой грани до плоскости основания пирамиды равно b. Определить объем пирамиды.
E
A1 B1
K |
|
17x |
L |
|
|
C1 |
|
A |
9x |
10x |
B |
|
|||
|
|
M

 C
C
Рис. 84
Решение. Так как объем VA1ABC 288
см3, то VABCA1B1C1 3VA1ABC 864 см3. Пусть
треугольник KLM указанное в условии сечение, перпендикулярное ребрам призмы (см. рис. 84). Используя формулы
VABCA1B1C1 l S , Sбок l P ,
18.02.2011 |
49 |

 F
F



 A
A
K
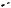







D H O
 B
B
C
Рис. 85
Решение. Пусть сторона основания данной пирамиды ABCDE равна x, основание высоты пирамиды обозначим через О, основание апофемы к стороне AD –
через K (см. рис. 85). Тогда OK x , вы- 2
сота EK в равностороннем треугольнике
равна x 3 . Из прямоугольного тре- 2
угольника EOK находим
www.alexlarin.narod.ru

Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
OE 
 x2
x2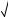 3 2 2x 2 x2
3 2 2x 2 x2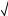 2 .
2 .
Если F – центр боковой грани, Н – основание перпендикуляра, опущенного из точки F на основание пирамиды, то FH b. Из подобия треугольников EOK и FHK получаем
EO EK 3 и EO 3 FH .
FH FK 1
Отсюда |
|
x 2 |
3b, |
x 3 |
|
b. |
Значит, |
|
|
2 |
|||||||
2 |
||||||||
|
|
|
|
|
|
|||
площадь |
основания |
пирамиды |
равна |
|||||
18b2 , высота пирамиды – 3b, объем данной пирамиды равен
V1 18b2 3b 18b3 . 3
Ответ: 18b3 .
введение вспомогательного угла
Пример 81. В правильной четырехугольной пирамиде ABCDE (Е – вершина) через середины сторон АВ и AD проведено сечение, плоскость которого параллельна ребру ЕА. Найти объем пирамиды, если сторона основания равна a и площадь сечения S.
Решение. Плоскость сечения пересекает плоскости AED и АВЕ по прямым GH и FJ соответственно, параллельным АЕ. FG ||BD, так как FG – средняя линия в треугольнике ABD (см. рис. 86).
E
K
J 


 S
S



 H
H
C




 T
T





B

 Q
Q







 D
D
F
 R
R
 G
G
A
Рис. 86
В квадрате ABCD AС BD. Так как AQ – проекция АЕ на основание пирами-
18.02.2011
ды и |
|
AQ FG , то FGHJ – |
прямоуголь- |
||||||||||||||||||||||||||
ник. Плоскости FGH и BDE пересека- |
|||||||||||||||||||||||||||||
ются по прямой JH . |
|
|
EQ HJ S , |
||||||||||||||||||||||||||
|
Пусть |
AC FG R, |
|||||||||||||||||||||||||||
|
RS CE K , |
|
EAC . |
Так |
как |
||||||||||||||||||||||||
|
|
|
1 |
AQ |
|
a |
|
|
|
, |
|
|
|
|
|
|
|
|
|
||||||||||
|
RQ |
2 |
то |
из |
треугольника |
||||||||||||||||||||||||
2 |
|
|
|
4 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
RQ |
|
|
|
a |
|
|
. |
|
|||||||||
RQS получаем RS |
|
|
|
2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
4cos |
|
||||||||
|
Далее в треугольнике АЕС по теореме |
||||||||||||||||||||||||||||
Фалеса |
EK |
|
|
AR |
|
1 |
, а в треугольнике |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
EQC |
|
|
|
ED |
AC |
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
по |
|
|
|
теореме |
Фалеса |
имеем |
|||||||||||||||||||||
|
QT |
|
EK |
|
|
1 |
|
(Т – проекция точки K на |
|||||||||||||||||||||
|
|
EC |
|
||||||||||||||||||||||||||
|
QC |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
плоскость основания пирамиды), то есть
QT 1QC a 2 . Значит, 4 8
SK TQ a
 2 . cos 8cos
2 . cos 8cos
Площадь сечения равна
S SFGHJ SJKH
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5a2 |
|||
|
a 2 |
|
|
a 2 |
|
1 |
|
|
a 2 |
|
|
|
a 2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
2 |
|
|
4cos |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
8cos |
|
|
16cos |
||||||||||||||||||||||||
|
Отсюда cos |
5a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
16S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
sin |
|
|
|
256S2 25a4 |
|
|
|
|
|
|
|||||||||||||||||||||
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16S |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
tg |
|
|
|
256S2 25a4 |
. |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5a2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Высота пирамиды |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
EQ AQtg |
a |
|
|
tg |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и объем пирамиды |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
1 |
a2 |
a |
|
|
|
|
|
|
|
|
|
|
256S2 |
|
25a4 |
|
|
|
||||||||||||||
|
|
|
V |
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
5a2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
a
 512S2 50a4 . 30
512S2 50a4 . 30
Ответ: a
 512S2 50a4 . 30
512S2 50a4 . 30
50
www.alexlarin.narod.ru
