Saprikina_Analit_geometr

y = 1− 3 = −1, C (− 2; −1). Остаточно одержимо рівняння кола

(x + 2)2 + (y +1)2 = 20 .

Задача3. Заданарівностороннягіпербола x2 − y2 = 8 . Знайтирівняння еліпса, фокуси якого знаходяться у фокусах гіперболи, якщо відомо, що еліпс проходить через точку A(4; 6).

Розв'язання. Виходячиізвзаємногорозташуваннягіперболитаеліп-

Для еліпса, як і для гіперболи, відстань від центра до фокусів

Задача 4. Центром гіперболи є точка C (− 5; 0), один з фокусів збігається з початком координат. Знайти рівняння гіперболи, якщо відо-

мо, щовонавідтинаєвідосіординатхорду, довжинаякоїдорівнює 92 .

РІВЕНЬ В

Задача1. ДанокоординативершинтрикутникаОАВ: O (0; 0), A(2; 2), B (− 2; 2). Точка М рухається так, що сума квадратів її відстаней від трьох сторін трикутника залишається сталою і такою, що дорівнює 16. Знайти траєкторію точки М.

Розв'язання. Рівняння сторони трикутника OA: y = x; OB : y = = − x; AB : y = 2. Виберемо точку M (x; y) зі змінними координатами

шуканоїмножиниточок; MM1 , MM2 , MM3 – відстанівідточкиМдо сторін ОА, ОВ, АВ відповідно (рис. 5.14). За умовою задачі

= y 1− 2 . Перейдемо до координат: (x − y)2 + (x + y)2 + 2(y − 2)2 = 32.

Післяперетвореньодержиморівнянняеліпса x2 + (y −1)2 =1. 4 7

Задача 1. Точка B1 (3; −1) є кінцем малої осі еліпса, фокуси якого лежать на прямій y + 6 = 0. Скласти рівняння цього еліпса, знаючи його

ексцентриситет ε = 22 .

рівнює10, а ординатадодатна. Обчислитифокальнірадіусицієїточкита гострийкутміжними.

Задача 3. Рівняння асимптот гіперболи y = ± 12 x, одна з її точок

M (12; 3 3). Скластирівняннягіперболи.

одного. Знайти точки, однаково освітлені обома джерелами.

Задача 2. У точці N, що ближча до пункту В, розташована ворожа батарея. На постах спостережень А і В звуки її вибухів чути неодночасно: напостуАпізнішеТсекундами, ніжнапостуВ(АВ= 2с). Яквизначити ворожу батарею?

Практичне заняття № 6

Криві другого порядку. Парабола

Короткі теоретичні відомості

Параболоюназиваєтьсягеометричнемісцеточокнаплощині, рівновіддалених від даної точки F, яка називається фокусом, та прямої d, що називається директрисою. Вважається, що F d.

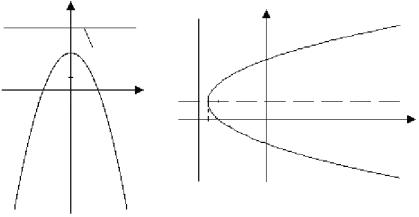
Парабола з вершиною в початку координат, яка симетрична віднос-

x2 = 2 py; x2 = − 2 py визначаютьпараболи, інакшеорієнтованівідносно координатних осей(див. рис. 6.1,б–г).

Примітка. Рівняннявигляду (y − y0 )2 = 2 p(x − x0 ) визначаєпараболу(див. рис. 6.1,д), яка паралельно зміщена відносно системи координат Oxy таким чином, що вершина параболи знаходиться в точці M 0 (x0 ; y0 ), вісь – паралельна осіОх.

Завдання для аудиторної роботи

РІВЕНЬ А

Задача 1. Скласти рівняння параболи, вершинаякоїзбігається зпочатком координат, якщо:

1) вісь симетрії параболи збігається з віссю Ох, а фокус знаходиться в точці F (5; 0);

2)параболасиметричнавідносноосіОу, аїїдиректрисамаєрівняння y +1 = 0;

3)парабола симетрична відносно осі Ох та проходить через точ-

ку A(−1; 3);

4)параболарозташованавнижнійпівплощинісиметричновідносно

осі Оу, а її параметр p = 34 .

Розв'язання

1. Рівнянняпараболимаєвигляд y2 = 2 px (див. рис. 6.1,а). Відстань

2. Канонічне рівняння цієї параболи x2 = 2 py (див. рис. 6.1,б).

= − 2 p(−1). Отже, рівнянняпараболи y2 = −9x.

4. Рівнянняцієїпараболибудемативигляд x2 = − 32 y (див. рис. 6.1,г).

Задача2. Знайтирівнянняпараболитаїїдиректриси, якщопарабола проходить через точки перетину прямої у – х = 0 і кола х2 + у2 + 8х = 0 та симетрична відносно осі Ох.

та A(− 4; − 4). Оскільки парабола симетрична відносно осі Ох, проходить через початок координат і точка А лежить у третій чверті, то її

рівняннямаєвигляд y2 = − 2 px. Підставляючи востаннєрівняннякоординати точки А, знаходимо р = 2. Отже, шукане рівняння параболи

y2 = − 4x, арівняння директриси x −1 = 0.

Задача3. ЗнайтиточкуперетинузвіссюОхпараболи, фокусомякої є точка F (2; 1), а директрисою пряма x − 3 = 0.

Розв'язання. Рівнянняпараболибудемошукатиувигляді (y − y0 )2 = = − 2 p(x − x0 ), оскільки вісь параболи перпендикулярна до директриси,

отже паралельна осі Ох. У точці A(3; 1) вісь параболи перетинає директрису (рис. 6.2).

уВершина параболи т. C (x0 ; y0 )

B(2; 0).

Задача4. Установити, щокожнезнаступнихрівняньвизначаєпараболутазнайтикоординатиїївершиниС, фокусаF, величинупараметрар

Рис. 6.3

70 Аналітичнагеометрія

метріїданоїпараболиєпряма y −1 = 0, віткинапрямленівправо. Фокус

квадрата обидві частини даного рівняння: y2 = (− 3 − 2x )2 = 9 (− 2x)=

= −18x. Остаточно y2 = −18x . Останнє рівняння визначає параболу

з вершиноювпочаткукоординат, розташованувлівійпівплощинісиметричновідносноосіOx (див. рис. 6.1,б). Заобластювизначенняграфіком

рівняння y = −3 − 2x буделишечастинапараболи y2 = −18x, розташована в третій чверті (рис. 6.4,а).

5

Рис. 6.4