Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет кораблестроения им. адм. Макарова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Saprikina

.pdf

Скачиваний:

Добавлен:

15.02.2015

Размер:

1.03 Mб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ Національний університет кораблебудування імені адмірала Макарова

Л.Т. Саприкіна, Т.А. Юрченко, А.М. Кузнецов, І.І. Ластовецька

МЕТОДИЧНІВКАЗІВКИ довиконаннятиповихрозрахунківта

індивідуальнихзавданьзвищоїматематики

Вдвохчастинах Частина І

Рекомендовано Методичною радою НУК

Миколаїв 2006

УДК517(076)

Методичні вказівки до виконання типових розрахунків та індивідуальнихзавданьзвищоїматематики: У2 ч. / Л.Т. Саприкіна,

Т.А. Юрченко, А.М. Кузнецов, І.І. Ластовецька. – Миколаїв: НУК, 2006. – Ч. 1. – 40 с.

Кафедравищоїматематики

Методичні вказівки містять завдання типових розрахунків та індивідуальних завдань з розділів курсу вищої математики, що вивчаютьсястудентаминапершомукурсі.

Кожне завдання подано 25 варіантами. До типових розрахунківнаданізразкиїхвиконання.

Рецензентканд. фіз.-мат. наукО.М. Шихватов

2	ВидавництвоНУК, 2006

Розділ I

Типовий розрахунок №1. ЛІНІЙНА АЛГЕБРА ІАНАЛІТИЧНАГЕОМЕТРІЯ

Завдання 1. Встановити, що система рівнянь має єдиний розв’язоктазнайтийого: а) задопомогоюоберненоїматриці; б) за формуламиКрамера; в) заметодомГаусса.

Варіант	Система		Варіант	Система

	x + y – z =	– 2,		x + 2 y + z = 4,
1		=1,	2
1	4x – 3y + z	=1,	2	3x – 5y + 3z =1,
	2x + y = 5			2x + 7 y – z = 8

	x + y – z =1,			x – 2 y + 3z = 6,
3			4
3	8x + 3y – 6z = 2,		4	2x + 3y – 4z = 20,
	– 4x – y +	3z = – 3		3x – 2 y – 5z = 6

	3x + 2 y + z = 5,			x – y + 3z = 3,
5			6		= 3,
5	2x + 3y + z = 1,		6	3x – 5y + z	= 3,
	2x + y + 3z = 11			4x – 7 y + z	= 4

	x + y + z = – 2,			x – y + z =1,
7			8
7	4x + 2 y + z = – 4,		8	2x + 3y – 2z = 6,
	9x + 3y + z	= – 8		x + y + 2z	= 0

	x – y + z = 7,			2x + 3y + 2z = 9,
9			10		=14,
9	2x + y – z = 2,		10	x + 2y – 3z	=14,
	– x – 3y + 2z = 7			3x + 4 y + z	=16

Продовження

Варіант		Система		Варіант				Система

	3x + 4 y + 2z = 5,				3x + 2 y – z = 2,
11			= 4,	12					= –10,
11	2x – y – 3z		= 4,	12	5x – y + 3z				= –10,
	x	+ 5y + z = 5			4x		+ y – 2z		= 0

	x + y + z = 6,				4x – 3y + 2z = 9,
13				14			+ 5y – 3z			= 4,
13	5x + 4 y + 3z = 22,			14	2x		+ 5y – 3z			= 4,
	10x + 5 y + z = 23				5x		+ 6 y – 2z			= 18

	2x – y – z = 4,				2x + 3y + 2z = 9,
15				16		+ 2y – 3z			=14,
15	3x + 4 y – 2z =11,			16	x	+ 2y – 3z			=14,
	3x – 2 y + 4z =11				3x		+ 4 y + z		=	16

	2x + y – 2z = – 3,				x + 2 y + 4z = 31,
17				18			+ y	+ 2z	= 29,
17	x – 2 y + z = 4,			18	5x		+ y	+ 2z	= 29,
	3x – y + 7z		=13		3x – y			+ z =10

	x + 2 y + z = 4,				2x – 3y + z = – 1,
19				20			+ y + z		= 6,
19	3x – 5y + 3z =1,			20	x		+ y + z		= 6,
	2x + 7 y – z		= 8		3x		+ y – 2z		=	–1

	2x – z =1,				x + y + z = 2,
21			=1,	22		+ 3y + z = 4,
21	2x + 4 y – z		=1,	22	x	+ 3y + z = 4,
	x – 8y – 3z		= – 2		x	+ y		+ 3z	=	0

	x	+ y + z = 3,			7x + 2 y + 3z =15,
23		+ 4 y + z = 6,		24
23	x	+ 4 y + z = 6,		24	5x – 3y + 2z =15,
	x	+ y + 4z	= 0		10x – 11y +				5z = 36

	4x – 3y – z = – 6,
25
25	2x + 5 y – 3z = 4,
	5x + 6 y – 2z =18

Завдання2. Встановити, приякомузначенніλ системамаєненульовірозв'язки. Знайтицірозв'язки.

Варіант	Система	Варіант	Система

	x + 2 y – (λ + 4)z = 0,		3x – 2 y + z = 0,
1		2		+ 15z = 0,
1	2x + y – 5z = 0,	2	5x – (10 + λ) y	+ 15z = 0,
	x – y – z = 0		x + 2 y – 3z = 0

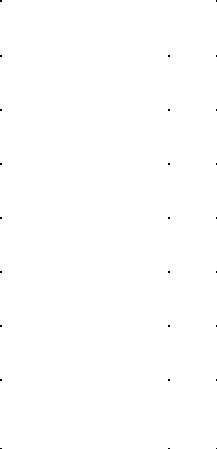
Продовження

Варіант		Система		Варіант			Система

	λx – y + 4z = 0,				2x + 3y + z = 0,
3		+ 2 y – z = 0,		4		+ 4 y + (1 + λ )z = 0,
3	x	+ 2 y – z = 0,		4	x	+ 4 y + (1 + λ )z = 0,
	5x + 3y + 2z = 0				3x		+ 7 y + 3z = 0

	λx – 3y + 2z = 0,				2x + y – 5z = 0,
5				6		+ (5 – λ ) y – 3z = 0,
5	–2x + 6 y – 4z = 0,			6	x	+ (5 – λ ) y – 3z = 0,
	3x – 9 y + 3z = 0				x	+ 2 y – 4z		= 0

	x – 6 y + 7z = 0,				4x + y + 3z = 0,
7				8		+ 2y – z = 0,
7	5x – 14 y + 15z = 0,			8	x	+ 2y – z = 0,
	x	+ (2 – λ) y – 3z = 0			5x		+ (5 – λ ) y		+ 2z = 0

	2x + 3y + z = 0,				5x + y – 2z = 0,
9				10
9	3x + (8 – λ) y + 3z = 0,			10	15x + 3y – (9 – λ )z = 0,
	x	+ 4 y + 2z = 0			x	+ y – 10z		= 0

	x – y – z = 0,				x + 2 y – (5 – λ)z = 0,
11				12				= 0,
11	x – 2z = 0,			12	x – 2 y + 2z			= 0,
	(1 – λ )x		+ 2 y – 4z = 0		3x – 2 y + z			= 0

	x + y = 0,				5x + 5 y + z = 0,
13			3z = 0,	14
13	4x + y +		3z = 0,	14	x + 4 y + 2z = 0,
	x	+ 2 y –	λz = 0		(5 – λ)x + 7 y + 3z = 0

	6x – λy – 3z = 0,				x + (4 – λ) y – 4z = 0,
15				16
15	– 2x + 6 y + z = 0,			16	4x + 5 y – 13z = 0,
	3x – 6 y – z = 0				x	+ y – 3z = 0

	2x – z = 0,				3x – y + 4z = 0,
17		+ 2 y – 3z = 0,		18
17	x	+ 2 y – 3z = 0,		18	(7 – λ )x + 3y + 2z = 0,
	(4 + λ )x – 14 y + 15z = 0				6x		+ 5y + z	= 0

	x	– y – z = 0,			2x		– y + z = 0,
	x	– y – z = 0,						+ 5 y – 5z = 0,
		+ λy + 2z = 0,			– (10 – λ)x			+ 5 y – 5z = 0,
19	x	+ λy + 2z = 0,		20	4x – 2 y + z			= 0
	3x + 7 y + 3z = 0

	x + 2 y – 4z = 0,				4x – 4 y + 3z = 0,
21				22		+ (6 – λ) y – 3z = 0,
21	4x + 5 y – (13 – λ)z = 0,			22	x	+ (6 – λ) y – 3z = 0,
	5x + 7 y – 16z = 0				x – 2 y + 2z			= 0

	2x – 3y + (5 + λ)z = 0,				2x + 3y + z = 0,
23		+ 2y – z = 0,		24		+ 4y + 2z		=	0,
23	x	+ 2y – z = 0,		24	x	+ 4y + 2z		=	0,
	5x + 3y – 2z = 0				(2		+ λ )x + 7 y		+ 3z = 0

Продовження

Варіант	Система		Варіант	Система
	x + y – 5z = 0,
25
25	x – y + z = 0,	+15z = 0
	(λ – 3)x – 3y	+15z = 0

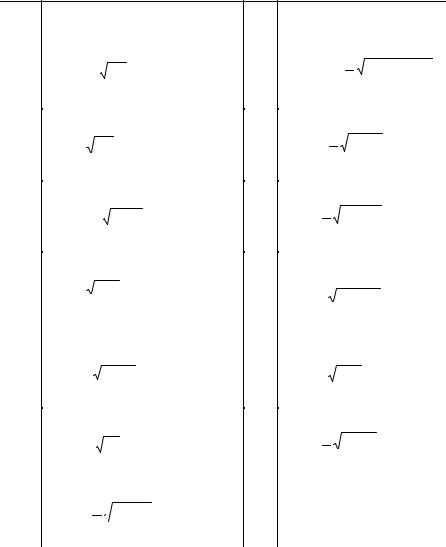
Завдання 3. Встановити, які лінії визначаються заданими рівняннями. Знайтихарактеристикицихлінійтапобудуватиїх.

Варі-

Рівняння

Варі-

Рівняння

ант

а) x2 + 4y2 = 4;

а) y2 = 5x + 10;

б) 9x2 – 25y2 – 18x – 100y – 316 = 0;

б) x = 5 –

y 2

+ 4 y −12 ;

в) x = –2

− y

в) 25x2 + 16y2 = 1

а) 16x2 + 25y2 + 32x – 100y –

а) y +

+ 2x + 7 = 0;

– 284 = 0;

б) x2 = 2 – y;

б) x =

49 − y2

;

в) x = –2 y2 −1

в) x2 – 4y2 = 16

а) x2 = 16y + 2;

а) x

= –2y – 2;

б) x = – 5 + 2

8 + 2 y − y 2 ;

б) x = 9 – 2 y2 + 4y + 8 ;

в) 16x2 + y2 = 64

в) –x

+ 4y = 4

а) y

= 4x

– 8;

а) y2 = 2x + 1;

б) x = –2 − 5 − 6y − y2 ;

б) y = –1 +

x 2

− 4x − 5 ;

в) –x2 + 9y2 = –9

в) x

+ 9y = 36

а) 16x2 – 9y2 – 64x – 18y + 199 = 0;

а) x2 = 2y + 2;

б) x = 4 − 2y ;

б) y = 1

–

− 6x − x 2 ;

в) 9x2 + 4y2 = 36

в) 4x2 – 7y2 = –28

а) x2 = 3y – 6;

а) 9x2 – 16y2 + 90x + 32y –

– 367 = 0;

б) x = – 4

+ 6y ;

б) y = x2 – 5;

в) x2 + 9y2 = 81

в) x2 + 6y2 = 24

Продовження

Варі-

Рівняння

Варі-

Рівняння

ант

а) 5x2 + 9y2 – 30x + 18y+ 9 = 0;

а) y2 = –12 – 6x;

б) x = –5 − y ;

14 б) y = –7 + 2 16 + 6x − x 2

;

в) 6x2 – 8y2 = –24

в) –9x2 + 4y2 = 36

а) 16x2 – 9y2 – 64x – 54y – 161 = 0;

а) y? – 6y + 14y + 49 = 0;

15 б) x = 4 − y ;

16 б) x = – 4

y2 + 9 ;

в) x2 + 25y2 – 25 = 0

в) 4x2 + 7y2 = 28

а) x = 2y2 + 6y;

а) 2x2 – 4x + 2y – 3 = 0;

б) y = – 3 x 2 +1 ;

18 б) x = 1

49 − y2 ;

в) 4x2 + 9y2 = 36

в) 9x2 – 16y2 = 144

а) x

– y

– 6x + 10 = 0;

а) 4x2 + 9y2 – 8x – 36y + 4 =

= 0;

б) y =

− 7x ;

б) y = –

− 4x + 2 ;

в) 9x

+ 25y

= 1

в) y2 – 9x2 = 9

а) 16x2 + 25y2 – 32x + 50y –

а) x2 – 9y2 + 2x + 36y – 44 =

– 359 = 0;

= 0;

б) y = – 2x + 2 ;

22 б) x = – − 3y ;

в) x2 – 4y2 = –16

в) 9y2 + 4x2 – 36 = 0

а) 4x2 + 3y2 – 8x + 12y – 32 = 0;

а) x2 – 6x – 4y + 29 = 0;

б) x = – 3y ;

24 б) y = 2

x 2 + 9 ;

в) – 5x2 + 9y2 = –45

в) 5x2 + 9y2 = 45

а) y2 – 10x – 2y – 19 = 0;

25б) x = – 34 y2 + 16 ; в) 16x2 + y2 = 16

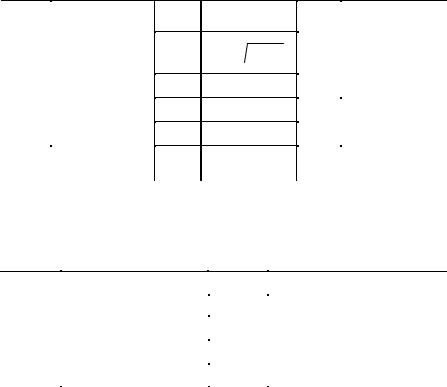
Завдання 4. Побудувати лінію, задану рівнянням у полярній системікоординат. Знайтиїїрівнянняудекартовійсистемі(додатня піввісь Оx співпадає з полярною віссю, полюс – з початком координат).

	Варі-	Рівняння
	ант	Рівняння
	ант
	1	ρ = 1 + cosϕ
		2
	2	ρ = 3sinϕ

	3	ρ = cos2ϕ

	4	ρ = 3(1 + sinϕ)

	5	ρ = 2(1 – cosϕ)

	Варі-	Рівняння
	ант	Рівняння
	ант

6ρ = 3 cos2 ϕ

7ρ = 3 + sinϕ

8ρ = 2cos2ϕ

9ρ = 1 + cos2ϕ

10 ρ = 3cos22ϕ

Варі-		Рівняння
ант

11	ρ =		3
			2 + sin ϕ


12	ρ = 2sin22ϕ
13	ρ = 4cosϕ

14	ρ = 2 + sinϕ

15	ρ =		1
			2 + cos ϕ

Записатирівняннязаданоїлініїуполярнихкоординатах(додатня піввісь Оx співпадає з полярною віссю, полюс – з початком координат) тапобудуватицюлінію.

Варіант	Рівняння

16	(х2 + у2) 2 = 20х3
17	(х2 + у2) 2 = 8у3
18	(х2 + у2)2 = 4(х2 – у2)
19	(х2 + у2)2 = 16(х2 – у2)
20	(х2 + у2) 3 = 4х2у2

Варіант	Рівняння

21	(х2 + у2) 2 = – 4х3
22	(х2 + у2) 2 = 18ху
23	(х2 + у2) 3 = x4
24	(х2 + у2) 3 = y4
25	(х2 + у2) 3 = (х2 – у2) 2

Зразоквиконаннятиповогорозрахунку№1

Завдання 1. Встановити, що система рівнянь

x – 2 y + 2z = 5,

– 3x + 8 y – 10z = –25,

4x – 3y + z = 1

має єдиний розв'язок та знайти його: а) за допомогою оберненої матриці; б) заформуламиКрамера; в) заметодомГаусса.

Розв’язання

Обчислимо визначник системи:

1 –2 2 ∆ = – 3 8 –10 = 8 + 80 +18 – 6 – 64 – 30 = 6;

4 –3 1

∆ ≠ 0, тому система має єдиний розв'язок.

а) Матричним методом розв'язок системи знайдемо за формулою

				X = А–1 Н,
		x
де X =		y	– матриця-стовпець невідомих;
		z
		5
	–25			– матриця-стовпецьвільнихчленів; А–1 – матриця, обер-
H =	–25			– матриця-стовпецьвільнихчленів; А–1 – матриця, обер-
		1
		1
нена до матриці системи
					1	–2	2
					–3	8	–10
				A =	–3	8	–10	.
					4	–3	1
					4	–3	1

Оберненаматрицяіснує, оскільки∆ = detА≠ 0. Знайдемооберненуматрицю. Дляцьогообчислимоалгебраїчнідоповненняусіх елементівматриціА:

8 –10

= –22;

= –

–3

−10

= –37;

–3

= –23;

–3

– 4

–3

= –

–2

= –4;

= –7;

= –

–2

= –5;

–3

A =

–2

= 4;

A = –

= 4;

A =

1 – 2

= 2;

–10

–3

–10

–3

	1		A11
A–1 =	1		A
A–1 =			A
				12
	det	A		A
				13

Тоді

A	A		1	– 22		– 4	4
21	31	=	1		–37	– 7
A22	A32						4	.
A22	A32		6				4	.
A	A		6		– 23	–5	2
23	33

x			– 22		– 4	4	5			– 22		5	– 4(–25) +	4 1		–1
		1							1				– 7(–25) +
X = y	=			–37	– 7	4	–25	=			–37	5		4 1	=	–1 .
		6							6
				– 23	–5	2	1				– 23	5	– 5(–25) +			2
z														2 1

Отже, х = –1; у = –1; z = 2.

б) За формулами Крамера

x = ∆∆x ; y = ∆∆y ; z = ∆∆z ,

де ∆ x =	5	– 2	2	= –6;	∆ y =	1	5	2	= –6;
де ∆ x =	–25	8	–10	= –6;	∆ y =	–3	–25	–10	= –6;
	1	–3	1			4	1	1

	1	–2	5
∆ z =	–3	8	–25	= 12; ∆ = 6.
	4	–3	1

Звідси маємо: х = −66 = –1; у = −66 = –1; z = 126 = 2.

в) Метод Гауcса

Прямийхід. Виключаємоневідомізрівняньсистеми, зводячиїї дотрикутноговигляду:

x – 2 y + 2z = 5		(I)	x – 2 y + 2z = 5
	–3x + 8y – 10z = –25	+ (I) 3		2 y – 4z = –10

4x – 3y + z = 1		+ (I) (– 4)		5 y – 7z = –19

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
29.08.201973.73 Кб0Rozd_6-1.doc
#
10.12.2018185.86 Кб3s1.doc
#
15.02.20158.14 Mб91s90mec7.pdf
#
15.02.20154.55 Mб18SADT.pdf
#
14.02.2015603.14 Кб285SANDCASTLE_Iris_Murdoch_1.doc
#
15.02.20151.03 Mб9Saprikina.pdf
#
15.02.20152.44 Mб29Saprikina_Analit_geometr.pdf
#
14.02.2015495.62 Кб8schod.doc
#
15.02.2015109.33 Кб64Schritte 2 - Lernwortschatz.pdf
#
14.02.2015759.3 Кб6Shlahter_Holnov_Is-vo_dominirovat.doc
#
14.02.201547.79 Кб13shtamp_2_2.docx