Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет кораблестроения им. адм. Макарова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Saprikina_Analit_geometr

.pdf

Скачиваний:

Добавлен:

15.02.2015

Размер:

2.44 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1211 12 > Следующая >>>

Відповіді, розв'язання та вказівки до завдань для самостійної роботи							101
Задача 3. Розв'язання. Зведемо рівняння даної лінії до канонічного
вигляду 4(x2 − 2x)− 3(y2 − 4 y)− 32 = 0	4(x2 − 2x +1)− 4 − 3(y2 − 4 y +
+ 4)+12 − 32 = 0 4(x −1)2 − 3(y − 2)2 = 24		(x −1)2		−	(y − 2)2	=1. Одер-
	6
				8
жане рівняння визначає гіперболу з центром у точці C (1; 2), дійсною

a = 6 тауявною b = 2 2 півосями, звідки с =			а2 + b2 = 6 + 8 =				14.

Фокуси гіперболи знаходяться на прямій у = 2 і віддалені від центра на 14 одиницьвправоівліво, отже F1 (1− 14; 2), F2 (1+ 14; 2); ексцент-

риситет ε = c	=	14	=	7	; рівняння асимптот	y − 2 = ±	2	(x −1)
a		6		3			3
(рис. 17).
Задача 4. Відповідь: рис. 18.
y						y

y = 2		8
y = 2	2
	2	6
	1	6
O	1	x

x =1

	1
−5	−1−O1 1 x

	x = −5 − 2	8 +2 y − y2
	3
Рис. 17		Рис. 18
	РІВЕНЬ Б
Задача 1. Розв'язання.	Центром еліпса є точка C (3; − 6), осями
симетрії – прямі х = 3, у = – 6; канонічне рівняння			(x − x0 )2	+
симетрії – прямі х = 3, у = – 6; канонічне рівняння			a2	+
			a2

+ (y − y0 )2 =1 (a > b), b = 5 (переконатися самостійно). Ексцентриситет b2

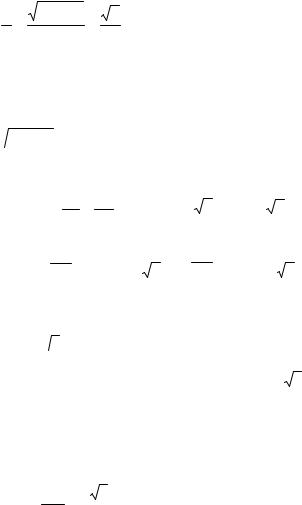
102							Аналітичнагеометрія

ε = c	=	a2 − b2		=	2	a2 = 50 . Рівняння еліпса остаточно має ви-
a		a			2
гляд	(x − 3)2		+ (y + 6)2			=1.
гляд		50	+ (y + 6)2			=1.
		50		25

Задача 2. Розв'язання. Знайдемо координати фокусів гіперболи:

с = a2 − b2 = 7 F1 (− 7; 0), F2 (7; 0). Фокальнірадіусиобчислимояквідстані F1C і F2C між двома точками. Координати точки C (xC ; yC ): xC =

= 10, y

y = 6 2 ; C (10; 6 2 );

F C

= 19,

F C

= 9.

C −

C = 1

Гострий кут α

між фокальними радіусами розрахуємо як кут між

векторами

CF = {−17; − 6

2} та CF = {− 3; − 6 2

}: α

= arccos

Задача 3. Розв'язання. З рівняння гіперболи випливає, що в заданій системі координат гіпербола матиме канонічне рівняння. Точ-

ка M (12; 3 3)належитьдопершоїкоординатноїчверті. З'ясуємо, яквона

розташованавідносноасимптоти y =

= 3 3, yасимптоти =

= 6 > yM

точка М знаходиться нижче від асимптоти, отже гіпербола

перетинаєвісьОх. Шуканерівняння

−

= 1; півосіa іb знайдемоіз

3)2

122

−

= 1,

системи

= 36, b

= 9. Остаточнерівняннягіпер-

боли

−

=1.

Відповіді, розв'язання та вказівки до завдань для самостійної роботи

103

РІВЕНЬ В

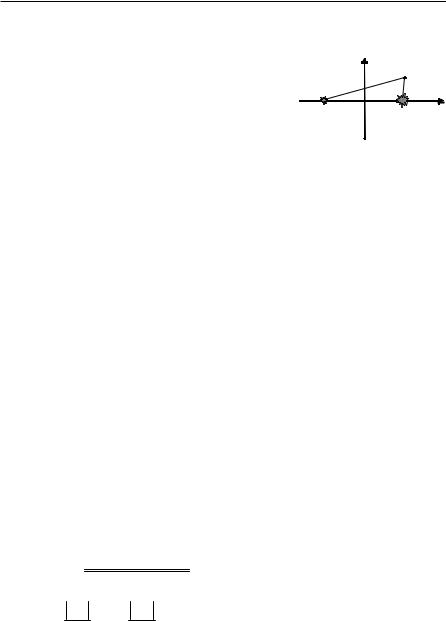
Задача 1. Розв'язання. Нехай точка M (x; y) – точка, рівноосвітле-

на обома джерелами (рис. 19).

З фізики відомо, що освітленість Е в заданій точці прямо пропорційна інтенсивності світлайоберненопропорційнавідстанівідточ-

ки до джерела світла. Отже,	E1	=	I		;
			AM	2

y	M (x; y)
	M (x; y)
I	n I
A(−b; 0) O	B(b; 0)	x

Рис. 19

n I

; E

= E

2 = n

2 – властивість

шуканого геометричного місця точок. Перейдемо до координат:

(x − b)2 + y2 = n (x + b)2 + n y2. Виконаємопевніперетворення: x2 − 2bx + b2 + y2 − nx2 − 2bnx − nb2 − ny2 = 0;

(1 − n)x2 − 2b(1 + n)x + (1 − n)y2 = (n −1)b2 |: (1 − n);

− 2b

+ n

x + b

+ n

− b

1 + n

+ y

= − b

;

− n

1 − n

n + 1

4nb2

x + b

+ y

n − 1

(n −1)2

Позначимо

n +1

= a > 0,

4nb2

= R2 > 0, отже шукана множина

n −1

(n −1)2

точок є коло (x + a)2 + y2 = R2 .

Задача 2. Розв'язання. Час поширення звуку до постів А і В відпо-

відно t1 = NAv , t2 = NBv , де v – швидкість поширення звуку в повітрі.

104	Аналітичнагеометрія

Тоді t − t	2	= NA	− NB = T
1	2	v	v
		v	v
ням гіперболи точка N (x; y)
		y
		N (x; y)
A(−c; 0)		O	B(c; 0)	x
		Рис. 20

NA − NB = vT = const. Згідно з означен-

належить правій вітці гіперболи, канонічне рівнянняякоїувибранійсистемікоординат

v2 T 2

, b

= c

− a

−

= 1, де a

точки А і В – фокуси гіперболи (рис. 20).

		Практичне заняття № 6
			РІВЕНЬ А
				9	; 0
Задача 1. Розв'язання. Фокус параболи F				2	; 0	(див. рис. 6.1,а). Аб-
				2
сцисаточкиМ: xM =	62	= 2	фокальнийрадіус r =				FM	= xM +	p	=	13		.
	62								p		13
	18								2			2
Задача 2	18								2			2


1. Відповідь: парабола			y2 = − 3(x − 2) з вершиною в точці C (2; 0),

параметром p = 32 , віткинапрямленівліво. Віссюсиметріїданоїпарабо-

ли є пряма у = 0; фокус		5			11
	F		; 0 , а рівняння директриси	x −		= 0
		4			4

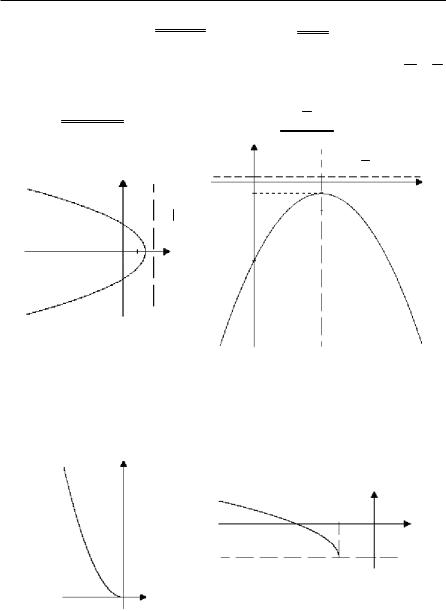
(рис. 21,а).

2.Розв'язання. Перетворимо дане рівняння до вигляду (x − x0 )2 =

=± 2 p(y − y0 ): y = − 16 (x2 −12x)− 7 = − 16 ((x − 6)2 − 36)− 7 = − 16 (x − 6)2 +

+6 − 7 = − 16 (x − 6)2 −1, або (x − 6)2 = −6( y +1) . Маєморівнянняпарабо-

Відповіді, розв'язання та вказівки до завдань для самостійної роботи

105

ли з вершиною в точці C (6; −1), параметром p = 3, вітки напрямлені

вниз. Віссю симетрії даної параболи є пряма х – 6 = 0. Оскільки 2p = 32,

то фокус F (6; − 2,5), а рівняння директриси y − 12 = 0 (див. рис. 21,б).

х− 11 = 0 4

0 F

уу − 12 = 0

0 6 х

– 1

Рис. 21

Задача 3. Відповідь

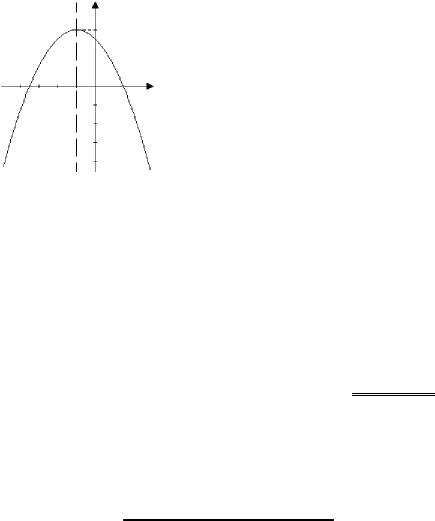
1.Частина параболи х2 = 3урозташована в другій чверті (рис. 22,а).

2.Частина параболи (у + 5)2 = –3(х + 7) розташована над прямою

у+ 5 = 0 (див. рис. 22,б).

– 7

– 5

0 x

а	б
	Рис. 22

106	Аналітичнагеометрія

Задача 4. Розв'язання. Рівняння параболи має вигляд (х + 1)2 = = – 2р(у – 3). Оскільки парабола відсікає на осі Ох хорду довжини 5, то

		3
вона проходить через точку	A		; 0
вона проходить через точку	A	2	; 0
		2

(рис. 23). Підставляючикоординатиточки А

		в рівняння параболи, знаходимо				p =	25	.
– 1 0 A	x	в рівняння параболи, знаходимо				p =	24	.
– 1 0 A	x						24
		Остаточно маємо	(x +1)2 = −	25	(y − 3).
		Остаточно маємо	(x +1)2 = −	12	(y − 3).
				12

	Рис. 23	РІВЕНЬ Б
	Рис. 23	Задача 1. Розв'язання. Будемо шукати
		Задача 1. Розв'язання. Будемо шукати

рівнянняхордиувигляді y −1 = k(x − 4). Длязнаходженняточокперети-

					y	2	= 6x,
					y		= 6x,	звідки
ну хорди з параболою розв'яжемо систему					y = k(x − 4)+1,			звідки
					y = k(x − 4)+1,

k 2 x2 − 2(4k 2 − k + 3)x + 16k 2 − 8k + 1 = 0. Оскільки точка A(4; 1) – сере-
	x + x		2(4k2 − k + 3)
дина хорди, то	1 2	=		= 4 (за теоремою Вієта), звідки
дина хорди, то	2	=	2k 2	= 4 (за теоремою Вієта), звідки
	2		2k 2

k = 3. Такимчином, рівнянняшуканоїхордимаєвигляд 3x − y −11 = 0.

Задача 2. Розв'язання

1.Знайдемо координати фокуса F (див. задачу 1 рівня Б аудиторної роботи). Одержимо F (− 3; − 3).

2.Складемо рівняння параболи за фокусом та рівнянням директриси (див. задачу 2 рівня Б аудиторної роботи). Одержимо повне рівняння

параболиувигляді 4x2 − 4xy + y2 + 32x + 34 y + 89 = 0 .

РІВЕНЬ В

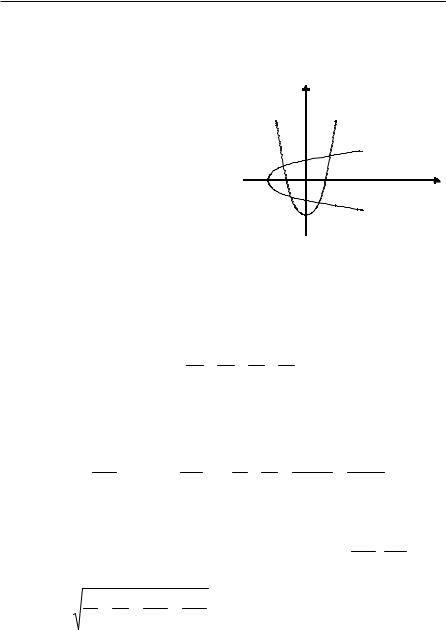
Задача 1. Відповідь: шуканою множиною точок є об'єднання множини точок парабол у2 = – 2х + 1 та у2 = 2х + 1.

Відповіді, розв'язання та вказівки до завдань для самостійної роботи

107

Задача 2. Доведення. Виберемо прямокутну декартову систему ко-

ординат Охутак, щоб осі Ох і Оу збіглися з осями парабол, а вітки пара-

болбулинапрямленівдодатнихнапрямкахкоординатнихосей(рис. 24).

Тоді рівняння парабол матимуть вигляд у = а

х2

– с

і х = а у2 – с , де

а1 > 0, a2 > 0.

Оскільки за умовою параболи

y = a1x2 – c1

перетинаються в чотирьох точках,

то c1 > 0, c2 > 0.

x = a2y2 – c2

Нехай М0 (х0 ; у0 ) – будь-яка

із чотирьох точок перетину пара-

– c2

бол. Тоді координати цієї точки

– c1

задовольняють систему рівнянь

х0

− с2 ,

Рис. 24

= а2 у0

= а х2

−

1 0

Зробившипевніперетворення, одержиморівняння

х2

+ у

2 −

у0

−

х0

−

с1 −

с2

= 0.

Виділяючиповніквадрати, отримаємо

с1

с2

х0

− 2а

+ у0

− 2а

+ а

(2а

+ (2а

)2 .

Отже, точка M0 лежить на колі з центром у точці

;

2а

і ра-

діусом R =

с1 +

с2

, що й треба було довести.

а1

а2

4а2

108 Аналітичнагеометрія

Практичне заняття № 7

					РІВЕНЬ А
Задача 1. Розв'язання
1.	x2	−	(y2 + z2 )	= 1	– двопорожниннийгіперболоїдобертаннянавко-
1.	4	−	9	= 1	– двопорожниннийгіперболоїдобертаннянавко-
	4		9
ло осі Ох (рис. 25,а).
			z		z
					1
			1
			− 21 O 2		x

y	x2		(y2 + z2 )	x 1
y	4	−	9	=1
	4	−	9	=1
				x =1 − z2
	а			б
	z			z
	1
	O 1		y	2
	O 1		y
	3

O 1

x		2			2
y = 1	− x		+ z2	y	2		2
		16		y	z =	4 − y	2
		16			z =	4 − y
в							г

	1	1
		1
	1 O	y
	1 O	Рис. 25
		Рис. 25

Відповіді, розв'язання та вказівки до завдань для самостійної роботи

109

x =1 − z2

– параболічний циліндр, твірна паралельна осі Оу, на-

1 − z

(див. рис. 25,б).

прямна – парабола

х2

– еліптичнийпараболоїд, орієнтованийувід'ємно-

у = 1 −

+ z2

му напрямку осі ординат, вершина в точці

A(0;1; 0), вісь симетрії Оу

(див. рис. 25,в).

z =

4 − y2

– круговийциліндр, твірніпаралельніосіОх, напрям-

4 −

(див. рис. 25,г).

на – z =

x = 0

−

= 0 – еліптичнийконус, вершинавпочатку коорди-

нат, вісь симетрії Оу (див. рис. 25,д).

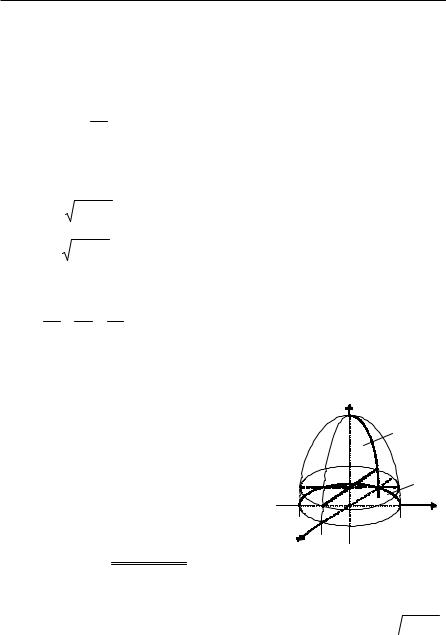
Задача 2. Розв'язання. Дана лінія являє собою лінію перетину кру-

гового параболоїда z = 5 – x2 – y2 та площини z = 1, що паралельна коор-

динатнійплощиніхОу(рис. 26).

Знайдемо рівняння циліндра, що

проектує L на площину xOy. Для цього

z =5−x2 − y2

виключимозрівняннясистемизміннуz:

5 − x2 − y2 = 1

x2 + y2 = 4 – круговий

z = 1

циліндр. Тодіпроекціяданоїлініїнапло-

+ y

= 4,

щину xOy – коло

z = 0

Рис. 26

РІВЕНЬ Б

Задача 1. Розв'язання

1. Визначимо тип поверхонь, завданих рівняннями y = − 9 − x2 ,

110 Аналітичнагеометрія

z = − y, z = 0: y = −		9 − x2		– круговийциліндр, твірніпаралельніосіОz,
			2
напрямна –	y = −	9 − x	2	, ; z = – у – бісектральна площина, що прохо-
напрямна –	y = −	9 − x		, ; z = – у – бісектральна площина, що прохо-
	z = 0

дить через вісь Ох; z = 0 – координатна площина хОу (рис. 27,а).

	z		z
z =−y	3	y =− 9 − x2	4
z =−y		y =− 9 − x2	x	z = 4 − x2 − y2
		y =	x	z = 4 − x2 − y2
		y =	2
			2
−3	O	y
	3 z = 0	y = x		y
x	3 z = 0		O	y
x		x		z = 0

	а					б
	z
		z = y2				Рис. 27
						Рис. 27
	O	2	x
	4	z = 0
y	2x + y = 4	z = 0
	в
2. z = 4 − x2 − y2 (y ≥ 0), y = x				, y = x,	z = 0:	z = 4 − x2 − y2 (y ≥ 0)
z − 4 = − (x2 + y2 )(y ≥ 0)			2
z − 4 = − (x2 + y2 )(y ≥ 0)			– частина кругового параболоїда з верши-

ною A(0; 0; 4), віссю симетрії Оz, орієнтованого у від'ємному напрямку

осіаплікат, розташованауІтаІІоктантах; y = 2x – площина, щомістить

вісь Оz; у = х – бісектральна площина, що містить вісь Оz; z = 0 – координатна площина хОу (див. рис. 27,б).

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1211 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.12.2018185.86 Кб3s1.doc
#
15.02.20158.14 Mб92s90mec7.pdf
#
15.02.20154.55 Mб18SADT.pdf
#
14.02.2015603.14 Кб285SANDCASTLE_Iris_Murdoch_1.doc
#
15.02.20151.03 Mб9Saprikina.pdf
#
15.02.20152.44 Mб29Saprikina_Analit_geometr.pdf
#
14.02.2015495.62 Кб8schod.doc
#
15.02.2015109.33 Кб64Schritte 2 - Lernwortschatz.pdf
#
14.02.2015759.3 Кб6Shlahter_Holnov_Is-vo_dominirovat.doc
#
14.02.201547.79 Кб13shtamp_2_2.docx
#
12.03.201627.84 Mб190Shustikova_T_v__Kulakova_V_a_-_Russky_Yazyk_-_Moy_Drug_bazovy_Uroven_-_2011.pdf