
- •Лабораторна робота № 1. Теоретична частина
- •Комбінаційні схеми і цифрові автомати
- •Контрольні запитання.
- •Теоретична частина Принципи побудови системи числення
- •Вибір системи числення
- •Загальні відомості про системи числення
- •Переведення чисел з однієї позиційної системи числення в іншу
- •Контрольні запитання.
- •Лабораторна робота № 3.
- •Теоретична частина
- •Контрольні запитання.
- •Лабораторна робота № 4.
- •Теоретична частина Двійкова арифметика
- •У еом всі чотири арифметичні дії зводяться до дії додавання.
- •Контрольні запитання.
- •Лабораторна робота № 5.
- •Теоретична частина Від’ємні числа у форматі байта
- •Контрольні запитання.
- •Лабораторна робота № 6.
- •Теоретична частина
- •Контрольні запитання.
- •Література.
Контрольні запитання.
Які системи числення називають позиційними?
Що називають основою системи числення?
Чому двійкова система числення стала основною для електронної техніки?
Дайте означення тетради та триади.
Сформулюйте алгоритми переведення чисел з однієї системи числення в іншу.
Виконайте вправи: Перетворити в десятковий код наступні двійкові числа: а) 0001; б) 0101; в) 1000; г) 1011; д) 1111; е) 0111.
Перетворити в десятковий код наступні двійкові числа: а) 1000 0000; б) 0001 0000; в) 0011 0011; г) 0110 0100; д) 0001 1111; е) 1111 1111.
Перетворити у двійковий код наступні десяткові числа: а) 23; б) 39; в) 55; г) 48.
Виконайте перетворення: 20410 =___2
1110 11102 = __10
Лабораторна робота № 3.
|
Тема: |
Переведення десяткових чисел в двійкові з записом у вісімковій та шістнадцятковій СЧ. |
|
Мета роботи:
Зміст роботи:
Організаційні та методичні вказівки: |
Набуття практичних навичок переведення чисел з однієї системи числення в іншу. Ознайомлення з можливостями калькулятора «Інженерний» стандартного офісного пакету MW для переведення чисел у системи числення, що застосовують у ЕОМ. Повторення теоретичних відомостей про системи числення та застосування навичок переведення чисел з однієї системи числення в іншу. Застосування засобів Microsoft Windows для виконання переведення чисел у двійкову та шістнадцяткову системи числення. Лабораторну роботу проводять після вивчення тем “Системи числення. Переведення чисел з однієї системи числення в іншу. ” з підгрупою студентів в два етапи: 1. Підготовчий етап: Вивчення можливостей виконання операцій над числами засобами калькулятора «Інженерний» стандартного офісного пакету MW. Повторення алгоритмів переведення чисел з однієї системи числення в іншу. 2. Виконавчий етап: Виконання індивідуальних завдань. Перевірка правильності виконання дій засобами Microsoft Windows. |
|
Технічне забезпечення: |
Персональний комп’ютер, дискета. |
|
Програмне забезпечення: |
Windows 98/XP, Microsoft Excel. |
|
Час: |
80 хвилин. |
Теоретична частина
Загальні відомості про системи числення
Система числення - сукупність прийомів і правил для зображення чисел за допомогою символів (цифр), що мають певне кількісне значення. Залежно від способів зображення чисел цифрами системи числення діляться на непозиційні і позиційні. В ЕОМ застосовуються позиційні системи числення. Непозиційні системи числення у ОТ не використовуються через свою громіздкість і складність правил виконання дій.
Позиційною
системою числення називається така, в
якій кількісне значення кожної цифри
залежить від її позиції (місця) в числі.
Прикладом може служити звичайна
(арабська) десяткова система числення.
Наприклад, число 373, представлене в
десятковій системі числення, має в
молодшому і самому старшому розрядах
цифру 3. Цифра 3 в старшому розряді має
вагу в 100 разів більше, ніж в молодшому
розряді. В позиційній системі числення
будь-яке число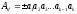 може
бути подано у вигляді наступної суми:
може
бути подано у вигляді наступної суми:
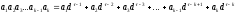 ,
де k
- загальна кількість розрядів в зображені
числа; ai-
цифра і
- го розряду; d
- основа системи числення;
,
де k
- загальна кількість розрядів в зображені
числа; ai-
цифра і
- го розряду; d
- основа системи числення;
і - порядковий номер розряду.
Цифри, необхідні для побудови системи числення, повинні задовольняти нерівність
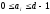 .
Основою системи числення d називається
кількість знаків або символів, що
використовуються для зображення числа
в даній позиційній системі числення.
За основу d
можна прийняти будь-яке число.
.
Основою системи числення d називається
кількість знаків або символів, що
використовуються для зображення числа
в даній позиційній системі числення.
За основу d
можна прийняти будь-яке число.
Використовування в ЕОМ позиційних системах числення дозволяє значно спростити зображення чисел і операції з ними.
Позиційні системи числення, що використовують в ЕОМ.
Від вибору системи числення при проектуванні ЕОМ залежать такі її характеристики, як швидкість обчислень, об'єм пам'яті, складність алгоритмів виконання арифметичних операцій. З погляду технічної реалізації якнайкращою є двійкова система числення, оскільки для побудови ЕОМ знайшли широке застосування двохпозиційні елементи. Двійкова система числення в ЕОМ є основною
системою числення, в якій здійснюються арифметичні і логічні перетворення інформації в пристроях ЕОМ. Будь-яке число з двійкової системи числення може бути переведено в десяткову за допомогою формули розкладання:
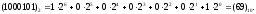
Основним недоліком використовування двійкової системи числення є необхідність перекладу початкових числових даних з десяткової системи числення в двійкову, а результатів виконання дій - з двійкової системи числення в десяткову. Операції, пов'язані з перекладами чисел в двійкову систему числення і назад, виконуються ЕОМ по спеціальних підпрограмах з використанням допоміжної двійково-десяткової системи числення.
Вісімкова система числення має основу d=8 і аі=0, 1, 2, 3, 4, 5, 6, 7.
Будь-яке
вісімкове число може бути представлене
за допомогою формули розкладання
десятковим еквівалентом, наприклад: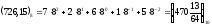
Запис команд програми у вісімковій системі числення у три рази коротше, ніж в двійковій.
Шістнадцяткова система числення має основу d=16 і аі=0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. При такому зображенні цифр у шістнадцятковій системі числення буква А зображає десять, B – одинадцять, З – дванадцять, D – тринадцять, E – чотирнадцять, F – п'ятнадцять.
Шістнадцяткова система числення так само, як і вісімкова, використовується при складанні програм для коротшого і зручнішого запису двійкових кодів – команд. Крім того в деяких ЕОМ шістнадцяткова система числення застосовується для представлення чисел в напівлогарифмічній формі.
Переведення чисел з однієї позиційної системи числення в іншу.
Переведення цілих чисел. Щоб перевести ціле число з однієї системи числення з основою d1 в іншу з основою d2 необхідно послідовно ділити це число і одержувані частки на основу d2 нової системи до тих пір, поки не вийде частка, менша за основу d2. Остання основа – старша цифра числа в новій системі числення з основою d2, а наступні за нею цифри – це залишки від ділення, записувані в послідовності, зворотній їх отриманню.
Примітка: При виконанні переведення чисел з однієї системи числення в іншу всі необхідні арифметичні дії виконуються в тій системі числення, в якій записано число, що переводиться.
Приклад 1.1 Перевести число 2510 у двійкову та вісімкову систему числення:
|
а) |
25 |
2 |
|
|
|
б) |
25 |
8 |
|
|
24 |
12 |
2 |
|
|
|
24 |
3 |
|
напрям читання |
1 |
12 |
6 |
2 |
|
|
1 |
|
|
напрям читання |
|
0 |
6 |
3 |
2 |
|
|
|
|
|
|
|
0 |
2 |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Шукані числа пишуться у вигляді (25)10=(11001)2=(31)8.
Зробимо перевірку переведення зворотнім переведенням шуканих чисел у десяткову систему числення:
а) (11001)2=124+123+022+011+120=16+8+0+0=1=(25)10.
б) (31)8=3·81+1·80=24+1=(25)10.
Переведення правильних дробів. Для того щоб перевести правильній дріб з системи числення d1 у систему з основою d2, необхідно послідовно множити вихідний дріб і дробові частини отриманих добутків на основу d2 нової системи числення. Правильний дріб у новій системі числення з основою d2 формується у вигляді цілих частин отриманих добутків починаючи з першого.
При переведенні правильних дробів з однієї системи числення у другу можна отримати дріб у вигляді нескінченного ряду. Процес переведення можна закінчити, якщо з’явиться дробова частина, яка має у всіх розрядах нулі, або буде досягнута задана точність переведення, тобто отримана потрібна кількість розрядів результату.
Якщо точність переведення дорівнює d2-q, то після q множень на d2 записують усі знайдені цілі частини у порядку їх знаходження. Знайдений запис буде подавати дробову частину числа у новій системі числення.
Приклад 2. Десятковий дріб 0,3126 перевести у двійкову систему числення з точністю до 2-4.
|
0,3126 |
|
0,6252 |
|
0,2504 |
|
0,5008 |
|
x 2 |
|
x 2 |
|
x 2 |
|
x 2 |
|
0,6252 напрям читання |
|
1,2504 |
|
0,5008 |
|
1,0016 |

Тобто шукане число запишеться у вигляді: (0,3126)10=(0,0101)2, а найбільша помилка буде 2-4.
Перевірку проведемо переведенням знайденого двійкового числа у десяткове:
(0,0101)2=02-1+12-2+02-3+12-4=1/4+1/16=6/16=(0,3125)10.
Приклад 3. Десятковий дріб 0,6 перевести у вісімкову систему числення з точністю 8-5.
|
0,6 |
|
0,8 |
|
0,4 |
|
0,2 |
|
0,6 |
|
x 8 |
|
x 8 |
|
x 8 |
|
x 8 |
|
x 8 |
|
4,8 |
|
6,4 |
|
3,2 |
|
1,6 |
|
4,8 |

напрям
При переведенні обмежуємося п’ятьма розрядами (q=5). Тоді шукане число запишеться у такому вигляді: (0,6)10=(0,46314)8, а найбільша помилка буде (≤8-5).
Переведення змішаних чисел. При переведенні змішаних чисел з одної системи числення у другу, необхідно у нову систему перекласти окремо його цілу та дробову частини по правилам переведення цілих чисел та правильних дробів, а потім два результати об’єднати в одне змішане число нової системи числення.
Приклад 4. Перекласти десяткове мішане число 159,75 у двійкову систему числення з точністю 2-3.
(159)10=(10011111)2;
(0,75)10=(0,11)2,
(159,75)10=(10011111,11)2.
Переведення чисел з вісімкової системи числення у двійкову і навпаки.
Для переведення числа з вісімкової системі числення у двійкову необхідно кожну цифру числа записати трьохрозрядним двійковим числом (триадою). Так як цифра вісім є степеню двійки (8=23), то вісімково-двійковий код співпадає з двійковим.
Приклад 5. Записати число (325,27)8 у двійковій системі числення.
(325,27)8=(011 010 101, 010 111)8-2=(11010101,01011)2.
Примітка. Незначні нулі зліва для цілих чисел і справа для дробів не записують.
Для переведення числа з двійкової системи числення у вісімкову необхідно розбити це число вправо та вліво від коми на групи по три розряди – тріади і замінити кожну групу відповідною цифрою вісімкової системі числення. Крайні неповні тріади доповнюють нулями.
Приклад 6. Записати число (10111011, 01101)2 у вісімковій системі числення.
(10111011,01101)2=(010 111 011, 001 010)8-2=(273,32)8.
Переведення чисел з шістнадцяткової системи числення у двійкову та навпаки.
Для переведення числа з шістнадцяткової системи числення у двійкову необхідно кожну цифру цього числа замінити тетрадою – чотирьохрозрядним двійковим числом. Так як шістнадцять є степеню двійки (16=24), то шістнадцятирічно-двійковий код співпадає з двійковим кодом.
Приклад 7. Записати число (C876,F3)16 у двійковій системі числення.
(C876.F3)16=(1100 1000 0111 0110, 1111 0011)16-2=
=(1100100001110110, 11110011)2.
Для переведення числа з двійкової системи числення у шістнадцяткову, необхідно розбити це число вправо і вліво від коми на тетради та представити кожну тетраду відповідною цифрою шістнадцяткової системи числення.
Приклад 8. Записати число (1011101101, 101101101)2 у шістнадцятковій системі числення.
(1011101101,101101101)2 =(0010 1110 1101, 1011 0110 1000)16-2=
=(2ED, B68)16.
Переведення чисел з десяткової системи числення в двійкову з проміжним переведенням у вісімкову або шістнадцяткову систему.
Для переведення чисел з десяткової системи числення у двійкову зручно використовувати проміжкове переведення у вісімкову або шістнадцяткову систему по загальним правилам, а потім найдене вісімкове або шістнадцяткове число записати у двійковій системі числення.
Приклад 9. Перевести (1972)10 у двійкову систему числення з використанням вісімкової (а) и шістнадцяткової (б) системі числення.
а) (1972)10=(3664)8;
(3664)8=(011 110 110 100)8-2;
(1972)10=(11110110100)2.
б) (1972)10=(7B4)16;
(7B4)16=(0111 1011 0100)16-2;
(1972)10=(11110110100)2.
Порядок виконання роботи
1. Повторіть алгоритми переведення чисел з однієї системи числення в іншу.
2. Ознайомтеся з можливостями калькулятора «Інженерний» стандартного офісного пакету MW для переведення чисел у системи числення, що застосовують у ЕОМ. Для цього необхідно виконати послідовність таких дій:
Пуск/Програми/Стандартні/Калькулятор та обрати у меню «Вид» опцію «Інженерний». Розгляньте позначення, що використовують для двійкової, десяткової, шістнадцяткової та десяткової систем числення.
3. Поясніть походження відповідних позначень.
4. В залежності від варіанту виконайте завдання:
І варіант ІІ варіант
4.1. Перевести двійковий дріб в систему числення з основою 8 та 16.
0.1010110011101 0.1100100011101
101110.10101111 100110.10111001
4.2. Перевести десяткові числа у двійкові, вісімкові та шістнадцяткові.
359,125 261,0625
4.3. Переведіть числа у десяткову систему числення.
101101,1112 ; 1111,00112;
327,28; 436,18;
1C,Fh. 2B,Dh.
5. Виконайте перевірку дій засобами калькулятора стандартного програмного пакету Microsoft Windows. Продемонструйте викладачу результати виконаної роботи.
6. Підготуйте звіт відповідно встановленого зразку.


