
- •Глава II. Векторная алгебра
- •§ 1. Векторы и основные линейные операции над ними
- •1. Векторные величины
- •2. Умножение вектора на скаляр
- •3. Единичный вектор
- •4. Сложение векторов
- •5. Вычитание векторов
- •§2. Линейная зависимость и независимость векторов. Базисы на плоскости и в пространстве. Прямоугольная декартова система координат
- •1. Линейная зависимость и независимость векторов
- •2. Базисы на плоскости и в пространстве
- •3. Прямоугольная декартова система координат
- •§3. Проекция вектора на ось. Координаты вектора. Компоненты вектора.
- •1. Проекция вектора на ось.
- •2. Компоненты вектора по координатным осям и координаты точки.
- •§ 4 Теоремы о проекциях вектора.
- •§ 5. Скалярное произведение и его свойства
- •1. Определение скалярного произведения
- •2. Необходимое и достаточное условие ортогональности двух векторов
- •3. Скалярное произведение векторов, заданных своими координатами
- •В силу свойства 4 получим
- •4. Угол между двумя векторами
- •§ 6. Векторное произведение и его свойства
- •1. Определение векторного произведения
- •2. Необходимое и достаточное условие коллинеарности двух ненулевых векторов
- •3. Векторное произведение векторов, заданных своими координатами
- •4. Механический смысл векторного произведения
- •§ 7. Смешанное произведение трёх векторов
- •2. Свойства смешанного произведения
- •§ 8. Двойное векторное произведение
2. Свойства смешанного произведения
1.
![]() .
.
Т.е. смешанное произведение не меняется при циклической перестановке перемножаемых векторов.
Действительно, каждое произведение имеет один и тот же модуль в силу геометрического смысла смешанного произведения. Знаки их также совпадают, так как ориентация тройки не меняется при циклической перестановке векторов.
2.
![]() .
.
Действительно, при перестановке двух соседних векторов модуль смешанного произведения не меняется, а знак меняется на противоположный, так как тройка меняет свою ориентацию.
3.
![]() .
.
Действительно,
в силу первого свойства:
![]() .
С другой стороны,
.
С другой стороны,![]() ,
откуда и следует окончательно:
,
откуда и следует окончательно:![]() .
Поэтому иногда смешанное произведение
обозначают
.
Поэтому иногда смешанное произведение
обозначают
![]() .
.
4. Если
![]() ,
,![]() ,
,![]() ,
то
,
то
 .
.
Действительно,

 .
.
§ 8. Двойное векторное произведение
Определение.
Двойным векторным произведением трёх
ненулевых векторов![]() ,
,![]() и
и![]() называется
называется![]() ;
если хотя бы один из векторов
;
если хотя бы один из векторов![]() ,
,![]() или
или![]() равен нулю, то
равен нулю, то![]() .
.
Итак,
мы видим, что двойное векторное
произведение представляет собою
векторную величину. Заметим, что объекты
типа
![]() часто встречаются в физике и механике.
Выведем простую форму для вычисление
двойного векторного произведения.
часто встречаются в физике и механике.
Выведем простую форму для вычисление
двойного векторного произведения.
Итак, допустим, что нам известны координаты векторов, т.е.
![]() ,
,![]() ,
,![]() .
.
Вычислим
![]() .
.
Обозначим
![]() ,
,![]() .
.
Очевидно,
что нас интересует вектор
![]() .
Известно, что вектор
.
Известно, что вектор![]() выражается через координаты векторов
выражается через координаты векторов![]() и
и![]() так:
так:
 ,
,
то есть
![]() ,
,![]() ,
,![]() .
.
В свою очередь, аналогично
![]() .
.
Подставим
в правую часть этого равенства полученные
выражения для
![]() ,
,![]() и
и![]() и, кроме того, выполним искусственное
преобразование, добавив и отняв к правой
части выражения
и, кроме того, выполним искусственное
преобразование, добавив и отняв к правой
части выражения![]() ,
,![]() ,
,![]() .
Получим:
.
Получим:
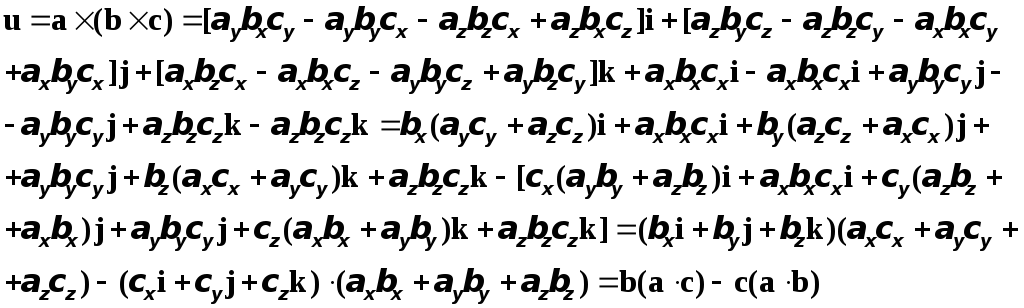
Итак,
получили:
![]() .
.
Отметим, что справа в скобках
стоят числа, равные скалярным произведениям
![]() и
и![]() ;
они являются коэффициентами линейной
комбинации векторов
;
они являются коэффициентами линейной
комбинации векторов![]() и
и![]() ,
через которые выражается двойное
векторное произведение
,
через которые выражается двойное
векторное произведение![]() .
Нетрудно заметить, что двойное векторное
произведение представляет собою вектор,
который лежит в той же плоскости, что и
вектора
.
Нетрудно заметить, что двойное векторное
произведение представляет собою вектор,
который лежит в той же плоскости, что и
вектора![]() и
и![]() ,
т.е. векторы
,
т.е. векторы![]() ,
,![]() и
и![]() компланарны.
компланарны.
Остановимся теперь на
вычислении выражения
![]() ,
которое, вообще говоря, также является
двойным векторным произведением.
Действительно:
,
которое, вообще говоря, также является
двойным векторным произведением.
Действительно:
![]()
т.е.
![]() представляет собою вектор, лежащий в
одной плоскости с векторами
представляет собою вектор, лежащий в
одной плоскости с векторами![]() и
и![]() .
Очевидно также, что
.
Очевидно также, что![]() .
.
Другие свойства двойного векторного произведения нетрудно проанализировать, принимая во внимание свойства скалярного и векторного произведения.
Пример 1. Показать, что точкиА (1,2,1), В (3,3,3), С (4,1,2) иD(5,4,5) лежат в одной плоскости.
Решение.Найдем координаты векторов![]() ,
,![]() и
и![]() .
.
![]() (2,1,2),
(2,1,2),![]() (3,-1,1),
(3,-1,1),![]() (4,2,4).
(4,2,4).
Если точки А, В, СиDлежат в однойплоскости, то и векторы лежат в одной плоскости (рис. 2.8.1), а тогда смешанное произведение этих векторов равно нулю.

Действительно,
(![]() ,
,![]() ,
,![]() )
=
)
= = 0,
= 0,
т.к. первая и вторая строки определителя пропорциональны.
Пример
2. Доказать, что векторы![]() ,
,![]() и
и![]() линейно зависимы и найти эту линейную
зависимость.
линейно зависимы и найти эту линейную
зависимость.
Решение.
(![]() ,
,![]() ,
,![]() )=
)= =0,
=0,
cледовательно,
векторы![]() ,
,![]() и
и![]() компланарны, а значит, они линейно
зависимы, т.е. существуют константы
компланарны, а значит, они линейно
зависимы, т.е. существуют константы![]() ,
,![]() и
и![]() такие, что
такие, что![]()
![]() +
+![]()
![]() +
+![]()
![]() =0,
т.е.
=0,
т.е.![]() (
(![]() +
+![]() +
+![]() )+
)+![]() (3
(3![]() +
4
+
4![]() +
+![]() )
+
)
+![]() (
(![]() +2
+2![]() -3
-3![]() )=
)=![]() ,
откуда следует: (
,
откуда следует: (![]() +
3
+
3![]() +
+![]() )
)![]() +
(
+
(![]() +
4
+
4![]() + 2
+ 2![]() )
)![]() + (2
+ (2![]() +
+![]() -3
-3![]() )
)![]() =
=![]() ,
т.к.
,
т.к.![]() ,
,![]() ,
,![]() - базисные векторы, то имеем такую
систему для нахождения
- базисные векторы, то имеем такую
систему для нахождения![]() ,
,![]() и
и![]() :
:


![]()
![]()

Здесь
![]() выступает в качестве параметра, и данная
система имеет бесчисленное множество
решений. Подставим
выступает в качестве параметра, и данная
система имеет бесчисленное множество
решений. Подставим![]() ,
,![]() в указанную выше линейную комбинацию:
в указанную выше линейную комбинацию:![]() .
Сократим на
.
Сократим на![]() .
Получим искомую линейную зависимость
.
Получим искомую линейную зависимость![]() .
.
