§ 5. Скалярное произведение и его свойства

1. Определение скалярного произведения

Определение. Скалярным произведением двух ненулевых векторовиназывается число, равное произведению длин этих векторов на косинус угла между ними, т.е.

.

Если хотя бы один из векторов равен нулю, то скалярное произведение этих векторов равно нулю (по определению).

Если , то, так как.

Отсюда следует, что .

Заметим, что скалярное произведение называется скалярным квадратом и обозначается. Следовательно,=> . Заметим, что иногда скалярное произведение обозначают.

Свойства скалярного произведения

1. прпр

Действительно, пр, но пр,отсюда следует, что пр.

2. Переместительноеиликоммутативноесвойство:

.

Это свойство очевидно, так как .

3. Сочетательноеилиассоциативноесвойство относительно числового множителя:

4. Распределительноеилидистрибутивноесвойство относительного сложения векторов:

.

Доказательство.

прпрпрпрпр

Следствие.

2. Необходимое и достаточное условие ортогональности двух векторов

Напомним, что два ненулевых вектора иназываются ортогональными, если они образуют прямой угол, т.е.

.

Теорема.Для того, чтобы два ненулевых вектора были ортогональны, необходимо и достаточно, чтобы их скалярное произведение обращалось в нуль.

Доказательство. Необходимость. Пусть векторыиортогональны, тогда.

Достаточность. Пусть. Так как векторы ненулевые, то отсюда следует, что, а это и означает, что векторыиортогональны.

3. Скалярное произведение векторов, заданных своими координатами

Пусть ,. Очевидно, что;;;. 

В силу свойства 4 получим

.

В частности,

.

4. Угол между двумя векторами

Если и- ненулевые векторы, то, принимая во внимание определение вектора и п.4, получим такое выражение для угламежду векторамиaиb:

.

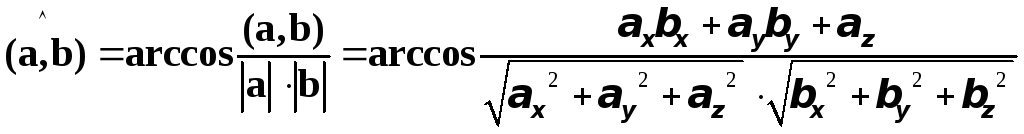Отсюда нетрудно получить условие ортогональности (перпендикулярности) двух векторов в координатной форме:

Механический смысл скалярного произведения

Если - сила, действующая на перемещенииS, то работаAэтой силы на указанном перемещении, как известно, равна, т.е.(рис. 3.5.1).

Рис. 3.5.1

Пример 1. Даны три точки

Найти и направляющие косинусы вектора.

Решение.а);

б) ;;

Пример 2. Дан вектор,,.

Найти длину вектора .

Решение.Найдём скалярный квадрат вектора:. Раскроем скобки, пользуясь свойствами скалярного произведения:

.

Пример 3. При каком значениивектораиортогональны.

Решение. Принимая во внимание условие ортогональности двух векторов, получим. Следовательно.

§ 6. Векторное произведение и его свойства

1. Определение векторного произведения

Определение. Векторным произведением ненулевых векторов и называется такой вектор, который удовлетворяет трём условиям:

1. , т.е. длина вектора численно равна площади параллелограмма, построенного на этих векторах.

2. Вектор перпендикулярен плоскости, в которой лежат векторы и .

3. Тройка ,,- правая(рис. 2.6.1)

Если хотя бы один из векторов и нулевой, то по определению. Заметим, что иногда векторное произведение двух векторовиобозначается символом.

Рис. 2.6.1

Свойства векторного произведения

1. .

Это очевидно, так как при перестановке векторов изменится ориентация тройки.

2. Свойство сочетательности относительно скалярного множителя:

.

(без доказательства)

3. Распределительное свойство относительно сложения векторов :

.

.

Следствие. .

То есть скобки можно раскрывать, как при обыкновенном умножении, не переставляя местами множители (без доказательства).