Matematika_Zaytsev_ch2

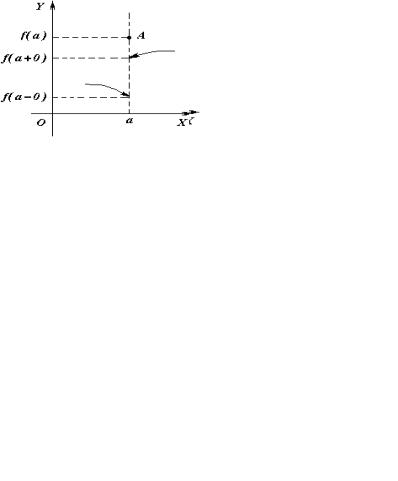
Разность f(a + 0) – f(a – 0) конечна, и её называют скачком функции в точке разрыва первого рода, а про функцию иногда говорят, что она терпит разрыв с конечным скачком.

Если скачок равен нулю, т.е. в точке a выполнено ещё и условие 3 непрерывности функции, а поэтому существует конечный предел функции в этой точке, то имеем точку устранимого разрыва.

вого замечательного предела f(0 + 0) = f(0 – 0) = 1. Следовательно, x = 0 – точка

уже будет непрерывной при x = 0.

На рисунке 9 приведены шесть графиков функций, имеющих разрыв первого рода в точке a. Буква А обозначает точку A(a, f(a)) графика функции. Стрелка обозначает, что концевая точка, где находится стрелка, выброшена. Случаи д) и е) иллюстрируют устранимый разрыв.

80

Рисунок 9 Все точки разрыва функции, не являющиеся точками разрыва первого рода,

относят к точкам разрыва второго рода.

Итак, точкой разрыва второго рода называют такую точку разрыва функции, в которой хотя бы один из односторонних пределов функции бесконечен или не существует.

Итак, данная функция в точке x = 0 имеет разрыв первого рода с конечным скачком, равным (–2).

Исследуем далее точку x = 1.

Так как f(1 – 0) = – ∞ , f(1 + 0) = +∞ , то в точке x = 1 разрыв второго рода.•

3.3 Свойства непрерывных функций

Вначале рассмотрим теоремы, которые определяют свойства непрерывных функций в точке.

Опираясь на теоремы о пределах и на определение непрерывности, читатель может легко убедиться в справедливости следующей теоремы.

Теорема 12 (арифметические операции над непрерывными функциями).

Если функции f(x) и g(x) непрерывны в точке а, то в этой же точке будут непрерывны и функции f(x) ± g(x), f(x)g(x), f ( x ) , последняя при условии g(a)≠0.

81

Теорема 13 (о непрерывности сложной функции).

Если функция y = f(x) непрерывна в точке а, а функция g(y) непрерывна в точке b = f(a), то сложная функция g(f(x)) непрерывна в точке а.

В силу непрерывности f(x) в точке a для этого δ найдется δ1, такое, что из ус-

ловия |x – a| < δ1 будет следовать |f(x) – b| < δ, а, значит, и |g(f(x)) – g(b)| < ε.

Последнее означает, что lim g( f ( x )) = g( b ) = g( f ( a )) , т.е. сложная функция

x→a

g(f(x)) непрерывна в точке a.

Замечания.

1) Отметим, что теорему 13 можно обобщить на суперпозицию более чем двух

т.е. для непрерывных функций операция предельного перехода перестановочна с операциями по вычислению значения функции в соответствующей точке. При вычислении предела сложной непрерывной функции удобно чередовать эти операции.

Рассмотрим наиболее важные свойства функций, непрерывных в каждой точке отрезка [a, b]. Множество таких функций обозначают С[a, b]. Здесь ограничимся только формулировкой соответствующих теорем, а основное внимание уделим обсуждению и иллюстрации этих свойств.

Теорема 14 (о нуле функции).

Пусть функция f(x) непрерывна на [a, b] и на концах этого отрезка принимает значения разных знаков. Тогда между a и b найдётся точка с, в которой функция обращается в нуль, т.е.

( f(x) C[a, b] ) ( f(a) f(b) < 0 ) c (a, b): f(c) = 0.

Теорема имеет простой геометрический смысл: если непрерывная линия графика лежит и ниже и выше оси ОХ, то эта линия пересекает ось ОХ (рисунок 10). Теорема имеет применение при решении уравнения f(x)= 0.

Действительно, если будет найден отрезок [a, b],

такой, что f(a) f(b)< 0, то, значит, внутри промежутка есть, по крайней мере, хотя бы один корень этого уравнения.

Рисунок 10

82

2. Исследуем на непрерывность показательную функцию y = ax. Для этого придадим аргументу x приращение ∆x , тогда приращение ∆y примет вид

∆y = a x+∆x − a x = a x ( a∆x − 1 ) .

Чтобы убедиться в непрерывности показательной функции, нужно проверить, что

lim ∆y = 0 или, что равносильно, lim a∆x = 1 . Это было показано в примере 4.

∆x→0 ∆x→0

3. Непрерывность логарифмической функции logax на интервале (0, +∞) как обратной к строго монотонной и непрерывной на R показательной функции ax с областью значений (0, +∞) следует из теоремы 17.

4. Степенную функцию xs, s R при x > 0 можно в силу основного логарифмического тождества записать в виде xs = es ln x , т.е. получим суперпозицию функций: y = f(x) = s lnx, непрерывной в интервале (0, +∞), и g(y) = ey, непрерывной на R. Из теоремы 13 о непрерывности сложной функции следует, что xs непрерывна на (0, +∞).

Рекомендуем читателю самостоятельно убедиться в непрерывности степенной функции в частных случаях:

xn, n N, непрерывна x R;

x–n, n N, непрерывна x R \ {0};

m

x n , m Z , n N , непрерывна в своей области определения.

5. Непрерывность функции sinx x R была установлена в примере 15.

точках x R, где cosx ≠ 0, т.е. непрерывна при всех x ≠ nπ + π2 , n Z .

Аналогично, функция ctgx = cossin xx непрерывна в тех точках x R, где sinx≠ 0,

т.е. при всех x ≠ nπ , n Z.

6. Обратные тригонометрические функции arcsinx и arccosx по теореме 17 непрерывны на отрезке [–1, 1]. Аналогично, функции arctgx и arcctgx непрерывны на R.

Таким образом, все основные элементарные функции непрерывны всюду, где они определены.

84

Функции из класса элементарных можно получить при помощи конечного числа алгебраических операций над основными элементарными функциями и их су-

перпозицией. Из теорем 12, 13 следует, что все элементарные функции непрерывны в своей области определения.

Замечание. Если функция составная, то она может иметь разрывы в тех точках, где меняется её аналитическое выражение.

3.5 Сравнение бесконечно малых и бесконечно больших функций

Как было показано, сумма, разность и произведение б.м. функций являются б.м. функциями. Этого, вообще говоря, нельзя сказать о частном: деление одной б.м. на другую может привести к различным результатам.

Рассмотрим правила сравнения б.м. функций.

Пусть α(x) и β(x) – б.м. функции при x→ a.

1. Функции α(x) и β(x) называют б.м. одного порядка при x → a и записывают

α( x ) = О( β( x )) , если при x→ a существует отличный от нуля конечный

x→a

2. Функцию α(x) называют б.м. более высокого порядка малости по сравнению

с β(x) при x→ a и записывают α( x ) = o( β( x )) , если существует и равен

x→a

нулю предел отношения α(x) /β(x), т.е.

В этом случае также говорят, что β(x) является б.м. более низкого порядка ма-

В некоторых случаях недостаточно знать, что одна из двух б.м. является б.м. более высокого порядка, чем другая. Нужно еще оценить, как высок этот порядок.

85

Вводится следующее правило: если α( x ) = O( β k ( x )) , то говорят, что

x→a

α(x) – б.м. k–го порядка малости относительно β(x) при x→ a, а число k > 0 – порядком малости.

Часто в качестве β(x) берут функцию x – a. Например, функция α(x)=1 – cosx

3. Особое место в сравнении б.м. функций одного порядка занимает случай, когда

lim α( x ) = 1 . x→a β( x )

Такие б.м. функции α(x) и β(x) называют эквивалентными при x→ a и обо-

значают α( x ) β( x ) .

x→a

Укажем наиболее важные свойства эквивалентных б.м., которые следуют из определения эквивалентности и свойств пределов:

Приведём таблицу основных эквивалентностей элементарных функций, кото-

рая во многих случаях позволяет упрощать вычисление пределов:

86

Следует иметь ввиду, что в таблице эквивалентностей аргумент x может быть любой б.м. функцией. Например,

Замечание. Для б.б. функций имеют место аналогичные правила сравнения. Рекомендуем читателю самостоятельно их рассмотреть.

Рассмотрим важную задачу.

Задача 1. Пусть Pn(x)=a0xn + a1xn–1+ . . .+ an и Qm(x)=b0xm + b1xm–1 +. . .+ bm

– многочлены степени m и n соответственно (n, m N), т.е. a0 ≠ 0, b0 ≠ 0.

При x→ ∞ многочлены Pn(x) и Qm(x) – б.б. функции. Сравним их.

87

Итак, можно сделать выводы:

при n < m многочлен Pn(x) имеет меньший порядок роста, чем Qm(x);

при n = m имеем Pn ( x ) = O( Qm ( x )) ;

x→∞

при n > m многочлен Pn(x) имеет больший порядок роста.

т.е. многочлен эквивалентен своему старшему члену при x→ ∞. •

4.ЗАДАЧИ

4.1Задачи с решениями

1. Найти lim x3 − x2 − x + 1 .

x→1

• Убеждаемся, что предел нельзя найти непосредственной подстановкой вместо x величины 1, в данном случае имеем отношение двух б.м. функций (случай

00 ).

Так как многочлены числителя и знаменателя дроби обращаются в нуль при x = 1, то, согласно теореме Безу, можно без остатка разделить эти многочлены на (x – 1):

Снова аналогичная ситуация. Можно снова произвести деление, или разложить многочлены на множители:

88

тель на произведение( 1 + x )( 1 + 3 x + 3 x2 ) , а затем сократим дробь на (1 – x):

Можно иначе решить эту задачу путём замены переменной. Полагая x=t6, получим t→ 1 при x→ 1, поэтому

• Здесь нельзя вычислить предел, поделив числитель на n2 и перейдя от предела суммы к сумме пределов. Хотя предел каждого слагаемого равен нулю при n →

∞, но и число слагаемых неограниченно возрастает. Напомним, что теорема о пределе суммы действительна только для конечного числа слагаемых.

89