
- •Методические указания
- •Общие методические указания
- •Примеры решения задач
- •Тема 1. Элементы аналитической геометрии на плоскости
- •Тема 2. Элементы линейной алгебры
- •Тема 3. Основы векторной алгебры
- •Вычислить длину вектора , если,,,.
- •Тема 4. Введение в математический анализ
- •Тема 5. Производная и дифференциал Правила дифференцирования:
- •Тема 6. Исследование поведения функции
- •Тема 7. Неопределенный интеграл
- •Тема 8. Определенный интеграл
- •Тема 9. Приложения определенного интеграла
- •Тема 10. Функции нескольких переменных
- •Тема 11. Кратные интегралы.
- •Тема 12. Ряды
- •Тема 13. Дифференциальные уравнения первого порядка
- •Тема 14. Дифференциальные уравнения второго порядка
- •Тема 15. Основы теории вероятностей
- •Тема 16. Элементы математической статистики
- •Контрольные задания для студентов - заочников экономического факультета
- •Контрольная работа №1
- •Тема: «линейная алгебра»
- •Тема: «аналитическая геометрия (прямая на плоскости)»
- •Тема: «элементы векторной алгебры»
- •Тема: «функции 2-х переменных»
- •Контрольная работа №2
- •Тема: «случайные величины»
- •Контрольные задания для студентов - заочников агрономического факультета
- •Контрольная работа 1.
- •Контрольная работа 2.
- •Контрольные задания для студентов - заочников биолого-технологического факультета и факультета ветеринарной медицины
- •Контрольные задания для студентов - заочников инженерного факультета и института природообустройства
- •Приложение
- •Литература
- •Содержание
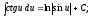
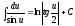 ;
;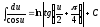 ;
;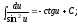
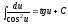 .
.Задача 18.
Найти неопределённые интегралы:
а)
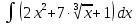 ;
б)
;
б)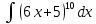 ;
;в)
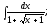 г)
г)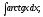 д)
д)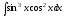 ;
;е)
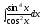 ; ж)
; ж)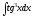 ;
з)
;
з)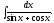
Решение:
Используем свойства и таблицу интегралов:
а)
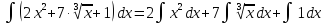 =
=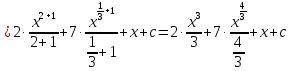 =
=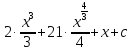 .
.б)
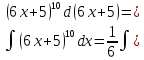
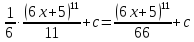
в) Сделаем замену

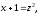
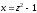 ,
,
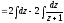 =
=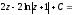
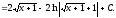
г) Интегрируем по частям по формуле:
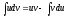 .
.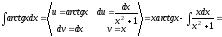
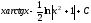 .
.д)
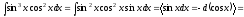
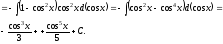
е)
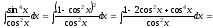
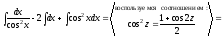
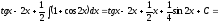
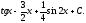
ж) Сделаем замену
 Получим
Получим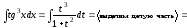
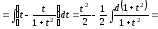
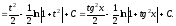
з) Сделаем замену
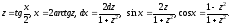
Получим
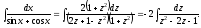
Последний интеграл есть интеграл от рациональной дроби. Выпишем эту дробь и разложим её на сумму простейших.
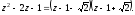
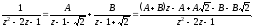
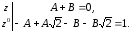
Решая систему, получим
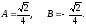
Тогда
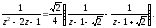
Следовательно,

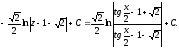
Тема 8. Определенный интеграл
Задача 19.
Вычислить интегралы:
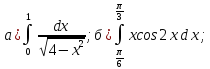
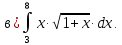
Решение:
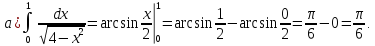
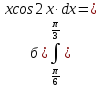
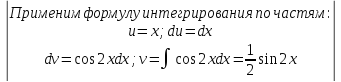 =
=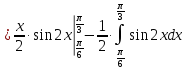 =
==
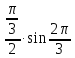 -
-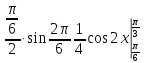 =
==
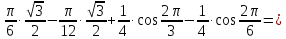
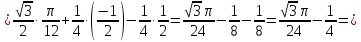
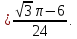
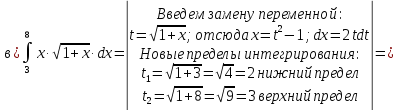
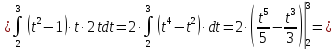
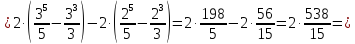
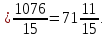
Тема 9. Приложения определенного интеграла
Задача 20.
Вычислить площадь фигуры, ограниченной линиями:
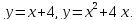
Решение:
Площадь
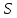 фигуры, ограниченная непрерывными
линиями
фигуры, ограниченная непрерывными
линиями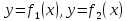 ,
,
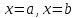 ,
при условии
,
при условии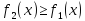 ,
определяется по формуле:
,
определяется по формуле: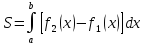
Для нахождения точек пересечения данных линий решаем систему уравнений
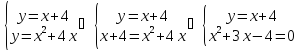
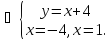
Итак, получили точки пересечения прямой и параболы: (
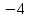 ;0)
и (1; 5).
;0)
и (1; 5).Построим фигуру, ограниченную указанными линиями.
Тогда
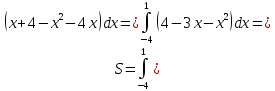
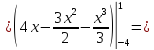
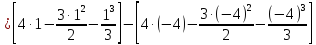
=
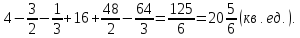

Рис. 2.
Задача 21.
Вычислить площадь поверхности эллипсоида, полученного вращением вокруг оси Ох эллипса:
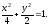 (1)
(1)Решение:
Площадь поверхности, образованной вращением вокруг оси Ох дуги кривой у = f(x) между точками с абсциссами х = а и х = b, вычисляется по формуле
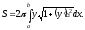 (2)
(2)Из уравнения эллипса (1) находим
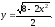
Производная
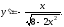 Используя
формулу (2), получим
Используя
формулу (2), получим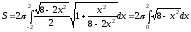
Чтобы вычислить последний интеграл, положим
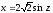
Тогда z = 0 при х = 0 и
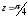 прих
= 2.
прих
= 2.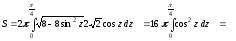
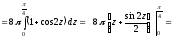
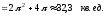
Тема 10. Функции нескольких переменных
Функцию z=f(x,y) можно дифференцировать, но при этом необходимо различать, по какой переменной это делается. Поэтому говорят о частных производных функции:
1) по переменной x z/x , f/x(x,y),
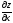 ,
,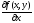 ;
;2) по переменной y z/y, f/y(x,y),
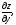
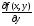 .
.Правила дифференцирования такие же, что и для функции одного переменного. Частная производная z/x означает, что приращение получает только переменная x при неизменном у. Частная производная z/y означает, что приращение получает только переменная y при неизменном x.
При дифференцировании частных производных по x или y получаем частные производные 2-го порядка:
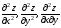 .
.Задача 22.
Вычислить частные производные 1-го порядка и 2-го порядка функции z: z=x3-5xy2-y3
Решение:
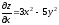 ,
,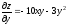 ,
,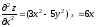 ,
,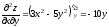 ,
,
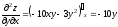 ,
,
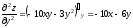 .
.Смешанные производные функции 2-х переменных равны, т.е
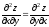 .
.Задача 23.
Записать полный дифференциал функции z=3ּx2+y3.
Решение:
Если x и y независимые переменные(∆x=dx, ∆y=dy), то полный дифференциал равен
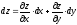 . Поэтому
. Поэтому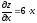 ,
,
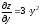 , иdz=6ּxּdx+3ּy2ּdy.
, иdz=6ּxּdx+3ּy2ּdy.Задача 24.
Исследовать на экстремум функцию
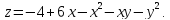
Решение:
1) Найдем критические точки, пользуясь необходимыми условиями экстремума:

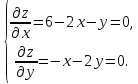
Решая систему, получаем критическую точку (4;-2).
2) Найдем производные второго порядка в критической точке и определяем характер критической точки:
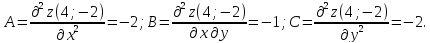 Получаем,
Получаем,
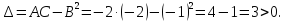 Так как
Так как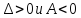 ,то
в точке (4;-2) функция имеет максимум:
,то
в точке (4;-2) функция имеет максимум: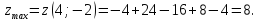
Тема 11. Кратные интегралы.
Задача 25
Дан интеграл
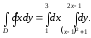
Требуется:
1) построить на плоскости хОу область интегрирования D;
2) изменить порядок интегрирования;
3) вычислить площадь области D при заданном и измененном порядке интегрирования.
Решение:
1. Пределы внешнего интеграла по переменной х — числа 1 и 3 — указывают на то, что область D ограничена слева прямой х = 1 и справа прямой х = 3.
Пределы внутреннего интеграла по переменной у указывают на то, что область D ограничена снизу параболой
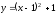 и сверху прямой
и сверху прямой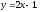 Построив эти линии на отрезке [1; 3],
получим областьD
(рис.
3).
Построив эти линии на отрезке [1; 3],
получим областьD
(рис.
3).  Рис.
3.
Рис.
3.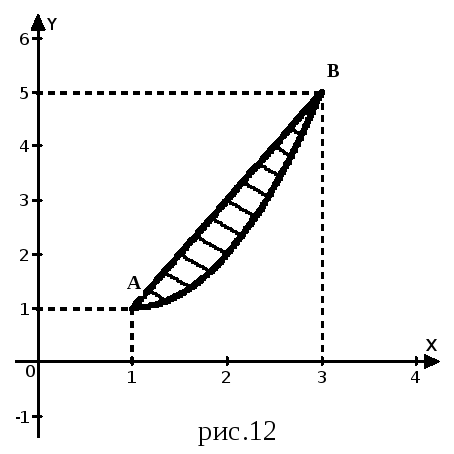
2. Чтобы изменить порядок интегрирования, установим пределы интегрирования для внешнего интеграла по переменной у. Как видно из рис. 12 наименьшее значение, которое принимает у в области D, равно 1 в точке А(1;1), а наибольшее значение равно 5 в точке В(3;5). Следовательно, внешний интеграл по переменной у будет иметь пределы: 1 (нижний предел) и 5 (верхний предел).
Определим пределы для внутреннего интеграла по переменной х.
Из уравнения прямой
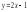 получаем
получаем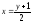 нижний предел.
нижний предел.Из уравнения параболы
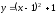 получаем
получаем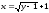 – верхний предел. Таким образом,
– верхний предел. Таким образом,
3. Вычислим площадь области D при заданном порядке интегрирования:
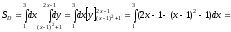
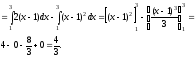
4. Вычислим площадь области D при измененном порядке интегрирования:
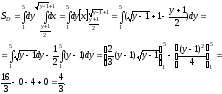
Тема 12. Ряды
Признак Даламбера.
Пусть дан ряд
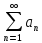 , причем
, причем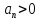 .
Если существует предел
.
Если существует предел ,
то при
,
то при
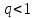 ряд сходится, при
ряд сходится, при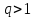 расходится.
расходится.Задача 26.
Исследовать ряд на сходимость, используя признак Даламбера
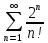
Решение:
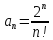 ,
,
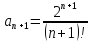 .
.Вычислим предел отношения
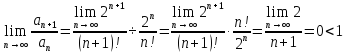 .
Следовательно, по признаку Даламбера
ряд сходится.
.
Следовательно, по признаку Даламбера
ряд сходится.Признак Коши.
Пусть дан ряд
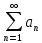 , причем
, причем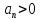 .
Если существует предел
.
Если существует предел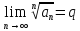 ,
то при
,
то при
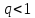 ряд сходится, при
ряд сходится, при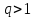 расходится.
расходится.Задача 27.
Исследовать ряд на сходимость, используя признак Коши
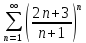 .
.Решение:
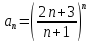 .
Вычислим предел
.
Вычислим предел
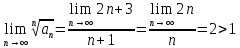 .
Следовательно, по признаку Коши ряд
расходится.
.
Следовательно, по признаку Коши ряд
расходится.Интегральный признак сходимости Коши.
Пусть дан ряд
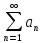 =
=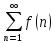 ,
причем
,
причем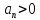 .
Элементы ряда являются значениями
некоторой функции
.
Элементы ряда являются значениями
некоторой функции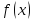 (положительной, непрерывной, невозрастающей
на
(положительной, непрерывной, невозрастающей
на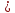 ).
Тогда
).
Тогда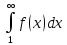 и
и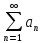 сходятся и расходятся одновременно.
сходятся и расходятся одновременно.Замечание.
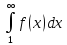 сходится, если существует конечный
предел
сходится, если существует конечный
предел
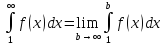 .
.Задача 28.
Исследовать ряд на сходимость, используя интегральный признак Коши
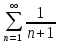 .
.Решение:
Рассмотрим функцию
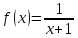 на
на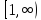 . Очевидно, что функция положительна,
непрерывна и невозрастающая на
. Очевидно, что функция положительна,
непрерывна и невозрастающая на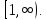 Исследуем на сходимость интеграл
Исследуем на сходимость интеграл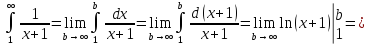
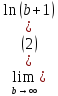 .
Значит, интеграл расходится, поэтому
и ряд расходится.
.
Значит, интеграл расходится, поэтому
и ряд расходится.Тема 13. Дифференциальные уравнения первого порядка
Задача 29.
Решить дифференциальное уравнение
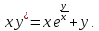
Решение:
Разделим данное уравнение на
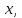 получим
получим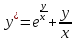 . Уравнение является однородным.
Применяем подстановку
. Уравнение является однородным.
Применяем подстановку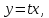 ,
где
,
где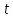 - некоторая функция аргумента
- некоторая функция аргумента .
Тогда
.
Тогда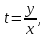
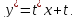
Уравнение примет вид
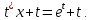 Отсюда
Отсюда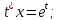
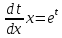 .
Чтобы разделить переменные, умножим
уравнение на дробь
.
Чтобы разделить переменные, умножим
уравнение на дробь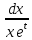 .
Получим
.
Получим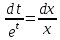 .
Это уравнение с разделенными переменными
относительно
.
Это уравнение с разделенными переменными
относительно и
и .
Интегрируя, находим общее решение этого
уравнения:
.
Интегрируя, находим общее решение этого
уравнения: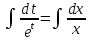 ;
;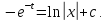
Выполним обратную замену
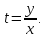 Следовательно,
Следовательно,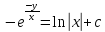 – общее решение данного уравнения.
– общее решение данного уравнения.Задача 30.
Получить общее решение уравнения
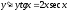 .
.Решение:
Данное уравнение является линейным, так как оно содержит искомую функцию
 и её производную
и её производную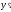 в первой степени и не содержит их
произведений.
в первой степени и не содержит их
произведений.Применяем подстановку
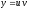 ,
где
,
где и
и - некоторые неизвестные функции аргумента
- некоторые неизвестные функции аргумента .
Если
.
Если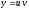 ,
то
,
то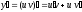 и данное уравнение примет вид
и данное уравнение примет вид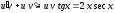 ,
,
или
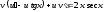 .
(1)
.
(1)Так как искомая функция
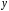 представлена в виде произведения двух
других неизвестных функций, то одну из
них можно выбрать произвольно. Выберем
функцию
представлена в виде произведения двух
других неизвестных функций, то одну из
них можно выбрать произвольно. Выберем
функцию так, чтобы выражение, стоящее в круглых
скобках левой части равенства (1),
обращалось в нуль, т.е. выберем функцию
так, чтобы выражение, стоящее в круглых
скобках левой части равенства (1),
обращалось в нуль, т.е. выберем функцию так, чтобы имело место равенство
так, чтобы имело место равенство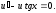 (2)
(2)При таком выборе функции
 уравнение (1) примет вид
уравнение (1) примет вид .
(3)
.
(3)Уравнение (2) есть уравнение с разделяющимися переменными относительно
 и
и .
Решим это уравнение:
.
Решим это уравнение: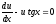 ;
;
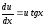 ;
; ;
;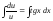 ;
;
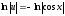 ,
,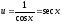 .
.Чтобы равенство (2) имело место, достаточно найти одно какое – либо частное решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрировании этого уравнения находим то частное решение, которое соответствует значению произвольной постоянной С=0. Подставив в (3) найденное выражение для
 ,
получим:
,
получим: ;
;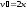 ;
;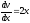 ;
;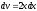 .
Интегрируя, получаем
.
Интегрируя, получаем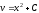 .
Тогда
.
Тогда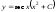 - общее решение данного уравнения.
- общее решение данного уравнения.Тема 14. Дифференциальные уравнения второго порядка
Задача 31.
Указать частные решения неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами со специальной правой частью, удовлетворяющее указанным начальным условиям:
а)
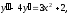
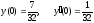 ;
;б)
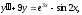
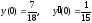 .
.При решении данных уравнений удобно использовать следующий алгоритм. Если дано неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами со специальной правой частью
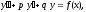 где
где
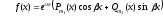 ,
где
,
где
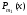 -
многочлен степени
-
многочлен степени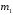 ,
,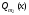 -
многочлен степени
-
многочлен степени .
Тогда общее решение уравнения ищется
в виде
.
Тогда общее решение уравнения ищется
в виде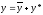 ,
где
,
где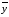 -
общее решение соответствующего
однородного уравнения,
-
общее решение соответствующего
однородного уравнения,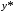 -
какое-либо частное решение неоднородного
уравнения.
-
какое-либо частное решение неоднородного
уравнения.
Чтобы найти
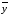 -
общее решение соответствующего
однородного уравнения
-
общее решение соответствующего
однородного уравнения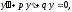 составляем характеристическое уравнение
составляем характеристическое уравнение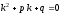 .
При решении которого возможны следующие
случаи:
.
При решении которого возможны следующие
случаи:
уравнение имеет действительные различные корни
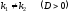 ,
тогда
,
тогда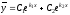 ,
где
,
где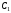 и
и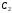 -
произвольные постоянные;
-
произвольные постоянные;уравнение имеет действительные равные корни
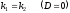 ,
тогда
,
тогда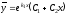 ,
где
,
где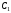 и
и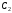 -
произвольные постоянные;
-
произвольные постоянные;уравнение имеет комплексные корни
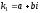 и
и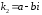
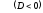 ,
тогда
,
тогда
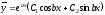 ,
где
,
где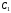 и
и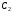 -
произвольные постоянные.
-
произвольные постоянные.
Если правая часть уравнения
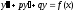 имеет специальный вид
имеет специальный вид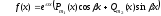 ,
где
,
где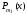 -
многочлен степени
-
многочлен степени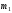 ,
,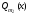 -
многочлен степени
-
многочлен степени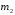 ,
тогда частное решение
,
тогда частное решение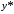 ищется в виде:
ищется в виде: ,
,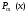 и
и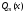 -
многочлены степени
-
многочлены степени ,
,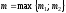 ,
а
,
а - кратность корня
- кратность корня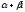 характеристического уравнения
характеристического уравнения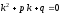 .
.
