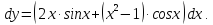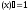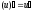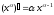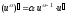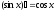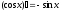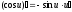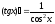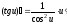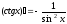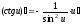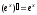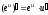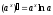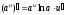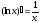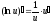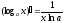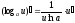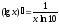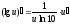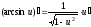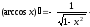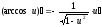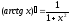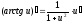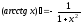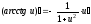- •Методические указания
- •Общие методические указания
- •Примеры решения задач
- •Тема 1. Элементы аналитической геометрии на плоскости
- •Тема 2. Элементы линейной алгебры
- •Тема 3. Основы векторной алгебры
- •Вычислить длину вектора , если,,,.
- •Тема 4. Введение в математический анализ
- •Тема 5. Производная и дифференциал Правила дифференцирования:
- •Тема 6. Исследование поведения функции
- •Тема 7. Неопределенный интеграл
- •Тема 8. Определенный интеграл
- •Тема 9. Приложения определенного интеграла
- •Тема 10. Функции нескольких переменных
- •Тема 11. Кратные интегралы.
- •Тема 12. Ряды
- •Тема 13. Дифференциальные уравнения первого порядка
- •Тема 14. Дифференциальные уравнения второго порядка
- •Тема 15. Основы теории вероятностей
- •Тема 16. Элементы математической статистики
- •Контрольные задания для студентов - заочников экономического факультета
- •Контрольная работа №1
- •Тема: «линейная алгебра»
- •Тема: «аналитическая геометрия (прямая на плоскости)»
- •Тема: «элементы векторной алгебры»
- •Тема: «функции 2-х переменных»
- •Контрольная работа №2
- •Тема: «случайные величины»
- •Контрольные задания для студентов - заочников агрономического факультета
- •Контрольная работа 1.
- •Контрольная работа 2.
- •Контрольные задания для студентов - заочников биолого-технологического факультета и факультета ветеринарной медицины
- •Контрольные задания для студентов - заочников инженерного факультета и института природообустройства
- •Приложение
- •Литература
- •Содержание
Тема 4. Введение в математический анализ
Задача 14.
Вычислить указанные пределы:
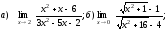
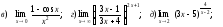
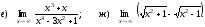
Решение:
а) Непосредственная
подстановка предельного значения
аргумента
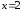 приводит к неопределенности вида 0/0,
чтобы раскрыть эту неопределенность,
разложим числитель и знаменатель на
множители и сократим члены дроби на
общий множитель
приводит к неопределенности вида 0/0,
чтобы раскрыть эту неопределенность,
разложим числитель и знаменатель на
множители и сократим члены дроби на
общий множитель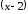 .
Так как аргумент
.
Так как аргумент только стремиться к своему предельному
значению 2, но не совпадает с ним, то
множитель
только стремиться к своему предельному
значению 2, но не совпадает с ним, то
множитель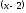 отличен от нуля при
отличен от нуля при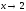 :
:
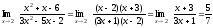 .
.
б) Непосредственная
подстановка предельного значения
аргумента
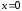 приводит к неопределенности вида 0/0,
чтобы раскрыть эту неопределенность,
домножим числитель и знаменатель на
сопряжённые выражения для числителя и
знаменателя (чтобы применить формулу
приводит к неопределенности вида 0/0,
чтобы раскрыть эту неопределенность,
домножим числитель и знаменатель на
сопряжённые выражения для числителя и
знаменателя (чтобы применить формулу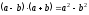 .
.
Тогда
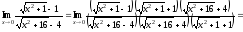
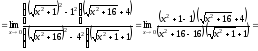
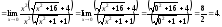
в)
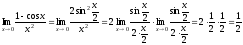 .
.
Использовали
первый замечательный предел
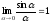 .
.
Искомый
предел можно найти иначе. Известно, что
при нахождении предела отношения двух
бесконечно малых величин можно каждую
из них (или только одну) заменить другой
бесконечно малой, ей эквивалентной, так
при
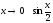 ~
~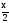 ,
то
,
то
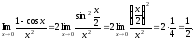
г) при
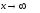 основание
степени
основание
степени
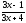 стремится
к 1, а показатель степени
стремится
к 1, а показатель степени
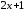 стремится к бесконечности. Следовательно,
имеем неопределенность вида
стремится к бесконечности. Следовательно,
имеем неопределенность вида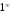 .
Представим основание в виде суммы 1 и
некоторой бесконечно малой величины:
.
Представим основание в виде суммы 1 и
некоторой бесконечно малой величины:
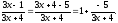
Тогда
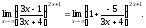
Используем второй замечательный предел

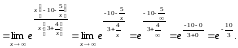
д) При
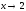 основание (3х–5) стремится к единице, а
показатель степени
основание (3х–5) стремится к единице, а
показатель степени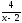 стремится к бесконечности.
стремится к бесконечности.
Положим
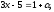 где
где
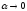 при
при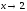 Тогда
Тогда
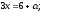
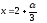 и
и
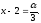
Выразив
основание и показатель степени через
 ,
получим
,
получим
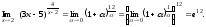
е)
Непосредственная подстановка предельного
значения аргумента приводит к
неопределенности вида
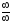 .
Чтобы раскрыть эту неопределенность,
разделим числитель и знаменатель на
.
Чтобы раскрыть эту неопределенность,
разделим числитель и знаменатель на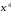 .
.
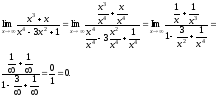
ж) Непосредственная
подстановка предельного значения
аргумента приводит к неопределенности
вида
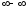 .
Чтобы раскрыть эту неопределенность,
умножим числитель и знаменатель дроби
на сопряженное выражение, чтобы применить
формулуa2–b2=(a–b)(a+b).
.
Чтобы раскрыть эту неопределенность,
умножим числитель и знаменатель дроби
на сопряженное выражение, чтобы применить
формулуa2–b2=(a–b)(a+b).
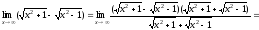
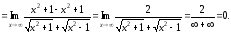
Тема 5. Производная и дифференциал Правила дифференцирования:
 ;
;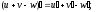
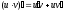 ;
;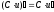 ;
;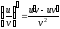 ;
;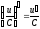 ;
;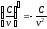 .
.
Таблица производных основных элементарных функций:
|
Производные основных элементарных функций |
Производные сложных функций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 15.
Определить
производные
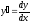 следующих функций:
следующих функций:
а)
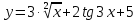
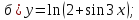
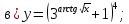
г)
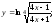 д)
д)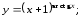
е)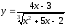 ;
ж)
;
ж)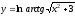 .
.
Решение:
Используем правила дифференцирования и таблицу:
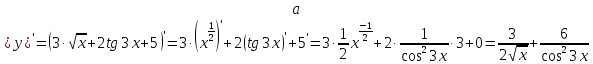 .
.
б) Последовательно применяя формулы и правила дифференцирования, получим:
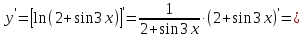
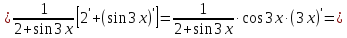
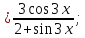
в)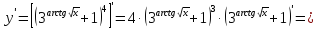
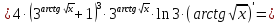
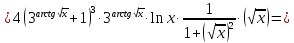
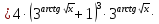
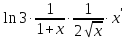 =
=
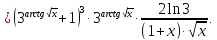
г) Пользуясь правилом логарифмирования, корня и дроби, преобразуем правую часть:
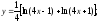
Применяя правила и формулы дифференцирования, получим:
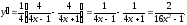
д) Предварительно прологарифмируем по основанию е обе части равенства:

Теперь
дифференцируем обе части, считая
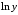 сложной
функцией от переменной х:
сложной
функцией от переменной х:
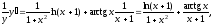
откуда
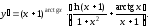
е) воспользуемся правилом дифференцирования
частного, получаем:
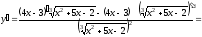
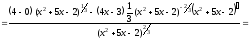
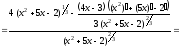
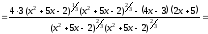
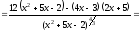
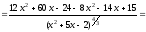
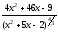 .
.
ж) Воспользуемся правилом дифференцирования сложной функции.
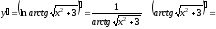
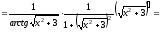
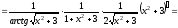
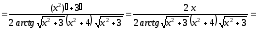
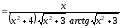 .
.
Задача 16.
Написать
дифференциал данной функции
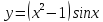 .
.
Решение:
Дифференциал
функции
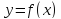 имеет вид
имеет вид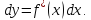
Вычислим производную, используя третье правило дифференцирования
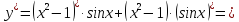
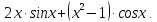
Тогда