- •Методические указания
- •Общие методические указания
- •Примеры решения задач
- •Тема 1. Элементы аналитической геометрии на плоскости
- •Тема 2. Элементы линейной алгебры
- •Тема 3. Основы векторной алгебры
- •Вычислить длину вектора , если,,,.
- •Тема 4. Введение в математический анализ
- •Тема 5. Производная и дифференциал Правила дифференцирования:
- •Тема 6. Исследование поведения функции
- •Тема 7. Неопределенный интеграл
- •Тема 8. Определенный интеграл
- •Тема 9. Приложения определенного интеграла
- •Тема 10. Функции нескольких переменных
- •Тема 11. Кратные интегралы.
- •Тема 12. Ряды
- •Тема 13. Дифференциальные уравнения первого порядка
- •Тема 14. Дифференциальные уравнения второго порядка
- •Тема 15. Основы теории вероятностей
- •Тема 16. Элементы математической статистики
- •Контрольные задания для студентов - заочников экономического факультета
- •Контрольная работа №1
- •Тема: «линейная алгебра»
- •Тема: «аналитическая геометрия (прямая на плоскости)»
- •Тема: «элементы векторной алгебры»
- •Тема: «функции 2-х переменных»
- •Контрольная работа №2
- •Тема: «случайные величины»
- •Контрольные задания для студентов - заочников агрономического факультета
- •Контрольная работа 1.
- •Контрольная работа 2.
- •Контрольные задания для студентов - заочников биолого-технологического факультета и факультета ветеринарной медицины
- •Контрольные задания для студентов - заочников инженерного факультета и института природообустройства
- •Приложение
- •Литература
- •Содержание
Тема 2. Элементы линейной алгебры
Для вычисления определителей 3-го порядка можно использовать правило треугольников
 =
=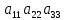 +
+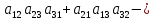
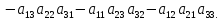
Задача 3.
Вычислить
определитель
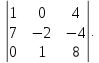
Решение:
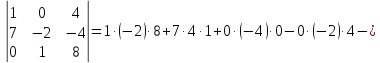
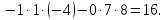
Задача 4.
Решить систему линейных уравнений:
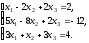
а) методом Гаусса; б) с помощью определителей (метод Крамера); в) с помощью обратной матрицы.
Решение:
а) Приведем данную систему к ступенчатому виду. Для этого используем преобразования расширенной матрицы данной системы, т. е. матрицы, составленной из коэффициентов при неизвестных и свободных членов. Для удобства столбец свободных членов этой матрицы отделим вертикальной чертой. Расширенная матрица данной системы имеет вид
 .
.
Умножим элементы первой строки матрицы на (–5) и результаты прибавим к элементам второй строки, затем умножим элементы первой строки на (–3) и результаты прибавим к элементам третьей строки. Получим матрицу
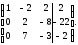
Разделив элементы второй строки на 2, получим
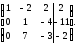
Элементы второй строки умножим на (–7) и результаты прибавим к элементам третьей строки. Получим матрицу
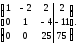 .
.
Восстановим систему по полученной матрице:
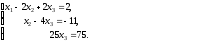
Откуда x3 = 3, х2 = 1 и х1 = -2.
б) Составим и вычислим следующие определители системы.
Определитель
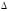 ,
составленный из коэффициентов при
неизвестных:
,
составленный из коэффициентов при
неизвестных:
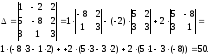
При
вычислении можно использовать правило
треугольников. Аналогично вычисляем
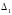 ,
полученный из
,
полученный из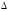 заменой первого столбца столбцом
свободных коэффициентов:
заменой первого столбца столбцом
свободных коэффициентов:
 ,
,
 и
и
 .
.
Тогда решения системы найдём по формулам:
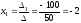 ,
,
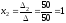 ,
,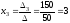 .
.
в)
Введём обозначения:
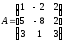 ,
,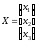 и
и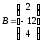 .
Тогда систему уравнений можно представить
в виде матричного уравнения
.
Тогда систему уравнений можно представить
в виде матричного уравнения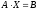 ,
которое решим по формуле:
,
которое решим по формуле: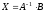 .
Найдём
.
Найдём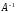 по следующему алгоритму.
по следующему алгоритму.
1)
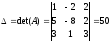 .
.
2)
вычислим алгебраические дополнения
элементов матрицы
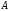 по формуле:
по формуле: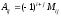 ,
где
,
где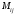 - определитель, полученный из
- определитель, полученный из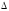 путём вычёркивания
путём вычёркивания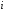 -ой
строки и
-ой
строки и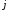 -го
столбца.
-го
столбца.
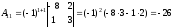 .
Аналогично вычисляем все остальные
алгебраические дополнения.
.
Аналогично вычисляем все остальные
алгебраические дополнения.
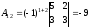 ,
,
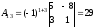 ,
,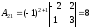 ,
,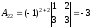 ,
,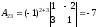 ,
,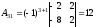 ,
,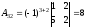 ,
,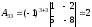 .
.
3) Из найденных дополнений составим матрицу:
 ,
получаем
,
получаем
 .
.
4)
Обратную матрицу получаем по формуле:
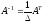 ,
т.е.
,
т.е.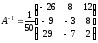 .
.
5)
Выполним проверку, покажем, что
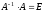 ,
где
,
где
 -
единичная матрица.
-
единичная матрица.




 .
.
Теперь найдём решение матричного уравнения
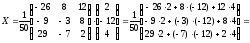
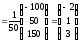 .
.
Тогда
решение системы:
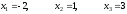 .
.
Задача 5.
Решить методом Гаусса систему уравнений
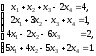
Решение:
Составим расширенную матрицу системы:

Умножив элементы первой строки последовательно на –2, –4 и –5. Полученные результаты прибавим соответственно к элементам второй, третьей и четвертой строк. Получим матрицу

Элементы второй строки умножим на 6 и результаты прибавим к элементам третьей строки, затем элементы второй строки прибавим к элементам четвертой строки. Получим матрицу

Элементы третьей строки разделим на –2 и затем элементы четвертой строки прибавим к элементам третьей строки. Получим матрицу

Теперь элементы третьей строки умножим на 13 и результаты прибавим к элементам четвертой строки. Получим матрицу

Следовательно, данную систему можно записать так:
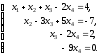
Откуда х4 = 0, х3 = 2, х2 = -1 и х1= 3.
Задача 6 .
Вычислить определитель, предварительно обратив в ноль все, кроме одного, элементы какого-нибудь столбца

Решение:
Переставим местами 1-й и 3-й столбцы. При этом определитель поменяет знак. Затем прибавим к элементам 2-й и 3-й строки соответствующие элементы 1-й строки. Определитель при этом не изменится. Получим
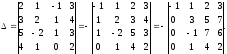
Мы обратили в ноль все, кроме одного, элементы 1-го столбца.
Разложим определитель по первому столбцу.
 =
=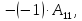 где
где
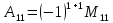 -
алгебраическое дополнение (см. задачу
4в).
-
алгебраическое дополнение (см. задачу
4в).
Вычислим
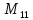 ,
используя правило треугольников:
,
используя правило треугольников:
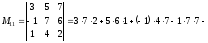
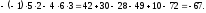
Значит,