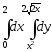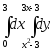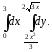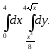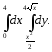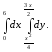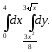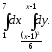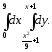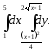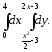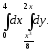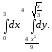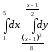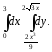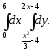- •Методические указания
- •Общие методические указания
- •Примеры решения задач
- •Тема 1. Элементы аналитической геометрии на плоскости
- •Тема 2. Элементы линейной алгебры
- •Тема 3. Основы векторной алгебры
- •Вычислить длину вектора , если,,,.
- •Тема 4. Введение в математический анализ
- •Тема 5. Производная и дифференциал Правила дифференцирования:
- •Тема 6. Исследование поведения функции
- •Тема 7. Неопределенный интеграл
- •Тема 8. Определенный интеграл
- •Тема 9. Приложения определенного интеграла
- •Тема 10. Функции нескольких переменных
- •Тема 11. Кратные интегралы.
- •Тема 12. Ряды
- •Тема 13. Дифференциальные уравнения первого порядка
- •Тема 14. Дифференциальные уравнения второго порядка
- •Тема 15. Основы теории вероятностей
- •Тема 16. Элементы математической статистики
- •Контрольные задания для студентов - заочников экономического факультета
- •Контрольная работа №1
- •Тема: «линейная алгебра»
- •Тема: «аналитическая геометрия (прямая на плоскости)»
- •Тема: «элементы векторной алгебры»
- •Тема: «функции 2-х переменных»
- •Контрольная работа №2
- •Тема: «случайные величины»
- •Контрольные задания для студентов - заочников агрономического факультета
- •Контрольная работа 1.
- •Контрольная работа 2.
- •Контрольные задания для студентов - заочников биолого-технологического факультета и факультета ветеринарной медицины
- •Контрольные задания для студентов - заочников инженерного факультета и института природообустройства
- •Приложение
- •Литература
- •Содержание
Контрольные задания для студентов - заочников инженерного факультета и института природообустройства
Студенты, изучающие математику три семестра (общий курс и студенты сокращенной формы обучения специальности «Инженерные системы в с/х и водоснабжении», берут задания из табл. 1 и 2.
Студенты, изучающие математику два семестра (все специальности, обучающиеся по сокращенной форме, кроме специальности «Инженерные системы в с/х и водоснабжении», берут задания из табл. 3 и 4.
Выбор таблицы происходит в соответствии с предпоследней цифрой учебного шифра: если цифра нечётная, то задания в таб.1, 3; если – чётная, то в таблице 2, 4. Последняя цифра шифра – вариант.
Таблица 1
Номер
варианта
Номера задач для контрольных работ
Работа 1
Работа 2
Работа 3
1
1
21
41
61
81
101
121
141
161
181
201
221
241
261
281
301
321
2
2
22
42
62
82
102
122
142
162
182
202
222
242
262
282
302
322
3
3
23
43
63
83
103
123
143
163
183
203
223
243
263
283
303
323
4
4
24
44
64
84
104
124
144
164
184
204
224
244
264
284
304
324
5
5
25
45
65
85
105
125
145
165
185
205
225
245
265
285
305
325
6
6
26
46
66
86
106
126
146
166
186
206
226
246
266
286
306
326
7
7
27
47
67
87
107
127
147
167
187
207
227
247
267
287
307
327
8
8
28
48
68
88
108
128
148
168
188
208
228
248
268
288
308
328
9
9
29
49
69
89
109
129
149
169
189
209
229
249
269
289
309
329
0
10
30
50
70
90
110
130
150
170
190
210
230
250
270
290
310
330
Таблица 2
Номер
варианта
Номера задач для контрольных работ
Работа 1
Работа 2
Работа 3
1
11
31
51
71
91
111
131
151
171
191
211
231
251
271
291
311
331
2
12
32
52
72
92
112
132
152
172
192
212
232
252
272
292
312
332
3
13
33
53
73
93
113
133
153
173
193
213
233
253
273
293
313
333
4
14
34
54
74
94
114
134
154
174
194
214
234
254
274
294
314
334
5
15
35
55
75
95
115
135
155
175
195
215
235
255
275
295
315
335
6
16
36
56
76
96
116
136
156
176
196
216
236
256
276
296
316
336
7
17
37
57
77
97
117
137
157
177
197
217
237
257
277
297
317
337
8
18
38
58
78
98
118
138
158
178
198
218
238
258
278
298
318
338
9
19
39
59
79
99
119
139
159
179
199
219
239
259
279
299
319
339
0
20
40
60
80
100
120
140
160
180
200
220
240
260
280
300
320
340
Таблица 3
Номер
варианта
Номера задач для контрольных работ
Работа 1
Работа 2
1
1
21
41
61
81
101
121
141
161
181
201
221
241
261
281
301
321
2
2
22
42
62
82
102
122
142
162
182
202
222
242
262
282
302
322
3
3
23
43
63
83
103
123
143
163
183
203
223
243
263
283
303
323
4
4
24
44
64
84
104
124
144
164
184
204
224
244
264
284
304
324
5
5
25
45
65
85
105
125
145
165
185
205
225
245
265
285
305
325
6
6
26
46
66
86
106
126
146
166
186
206
226
246
266
286
306
326
7
7
27
47
67
87
107
127
147
167
187
207
227
247
267
287
307
327
8
8
28
48
68
88
108
128
148
168
188
208
228
248
268
288
308
328
9
9
29
49
69
89
109
129
149
169
189
209
229
249
269
289
309
329
0
10
30
50
70
90
110
130
150
170
190
210
230
250
270
290
310
330
Таблица 4
|
| |||||||||||||||||
|
| |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
В задачах 1—20 даны координаты вершин треугольника ABC на плоскости.
Составить уравнения сторон АВ и ВС и высоты СD и их длины.
Определить величину угла В в радианах с точностью до двух знаков.
Составить уравнение медианы АЕ и указать координаты точки К пересечения этой медианы с высотой CD.
Составить уравнение прямой, проходящей через точку К, параллельно стороне АВ.
A(-7;-2), B(5;-11), C(9;11).
A(-4;8), B(8;-1), C(12;21).
A(-11;0), B(1;-9), C(5;13).
A(-9;10), B(3;1), C(7;23).
A(1;3), B(13;-6), C(17;16).
A(-8;7), B(4;-2), C(8;20).
A(2;1), B(14;-8), C(18;14).
A(-3;11), B(9;2), C(13;24).
A(3;6), B(15;-3), C(19;19).
A(0;5), B(12;-4), C(16;18).
A(-1;8), B(11;-1), C(9;13).
A(-5;9), B(7;0), C(5;14).
A(4;7), B(16;-2), C(14;12).
A(-9;6), B(3;-3), C(1;11).
A(-3;12), B(9;3), C(7;17).
A(-2;11), B(10;2), C(8;16).
A(5;2), B(17;-7), C(15;7).
A(-6;5), B(6;-4), C(4;10).
A(1;4), B(13;-5), C(11;9).
A(-4;10), B(8;1), C(6;15).
В задачах 21—40 решить систему трех уравнений с тремя неизвестными при помощи определителей (для студентов, обучающихся по сокращенной программе, систему решить любым способом).
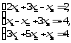
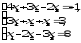 .
.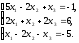
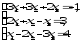
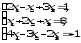
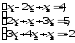
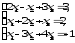
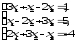
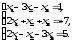
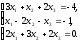
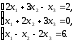
 .
.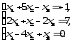 .
.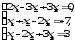 .
.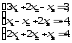
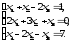
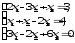
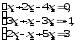
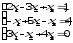
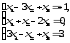
В задачах 41-60 даны координаты вершин пирамиды АВСD. Требуется: 1) записать векторы
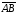 ,
, и
и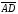 в системе орт и найти модули этих
векторов; 2) найти угол между векторами
в системе орт и найти модули этих
векторов; 2) найти угол между векторами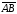 и
и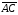 ;
3) найти проекцию вектора
;
3) найти проекцию вектора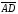 на вектор
на вектор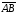 ;
4) найти площадь грани АВС; найти объем
пирамиды АВСD.
;
4) найти площадь грани АВС; найти объем
пирамиды АВСD.
A(2;-3;1), B(6;1;-1), C(4;8;-9), D(2; -1;2).
A(5;-1;-4), B(9;3;-6), C(7;10;-14), D(5; 1;-3).
A(1;-4;0), B(5;0;-2), C(3;7;-10), D(1;-2;1).
A(-3;-6;2), B(1;-2;0), C(-1;5;-8), D(-3;-4;3).
A(-1;1;-5), B(3;5;-7), C(1;12;-15), D(-1;3;-4).
A(-4;2;-1), B(0;6;-3), C(-2;13;-11), D(-4;4;0).
A(0;4;3), B(4;8;1), C(2;15;-7), D(0;6;4).
A(-2;0;-2), B(2;4;-4), C(0;11;-12), D(-2;2;-1).
A(3;3;-3), B(7;7;-5), C(5;14;-13), D(3;5;-2).
A(3;1;1), B(7;5;-1), C(5;12;-9), D(3;3;2).
A(0;1;3), B(1;-1;5), C(11;3;13), D(-2;1;7).
A(3;1;-2), B(4;-1;0), C(14;3;8), D(11;5;6).
A(-8;3;-1), B(-7;1;1),C(3;5;9), D(0;7;7).
A(2;-1;-4), B(3;-3;-2), C(13;1;6), D(10;3;4).
A(-4;5;-5), B(-3;3;-3), C(7;7;5), D(4;9;3).
A(-2;-3;2), B(-1;-5;4), C(9;-1;12), D(6;1;10).
A(-3;4;-3), B(-2;2;-1), C(8;6;7), D(5;8;5).
A(-5;2;-4), B(-4;0;-2), C(6;4;6), D(3;6;4).
A(-7;3;1), B(-6;1;3), C(4;5;11), D(1;7;9).
A(-6;-4;-3), B(-5;-6;-1), C(5;-2;7), D(2;0;5).
В задачах 61–80 вычислить указанные пределы:
а)
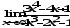 ;
б)
;
б)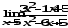 ;
в)
;
в)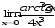 ;
г)
;
г)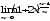 .
.а)
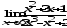 ;
б)
;
б)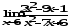 ;
в)
;
в) ;
г)
;
г)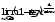 .
.а)
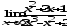 ;
б)
;
б)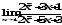 ;
;
в)
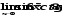 ;
г)
;
г)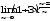 .
.
а)
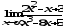 ;
б)
;
б)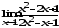 ;
;
в)
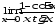 ;
г)
;
г)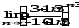 .
.
а)
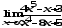 ;
б)
;
б) ;
;
в)
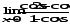 ;
г)
;
г)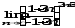 .
.
а)
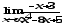 ;
б)
;
б)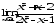 ;
в)
;
в)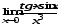 ;
г)
;
г)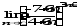 .
.а)
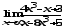 ;б)
;б)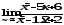 ;в)
;в)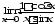 ;г)
;г)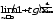 .
.а)
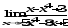 ;
б)
;
б)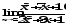 ;
;
в)
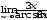 ;
г)
;
г)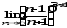 .
.
а)
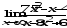 ;
б)
;
б)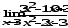 ;
;
в)
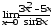 ;
г)
;
г)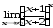 .
.
а)
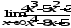 ;
б)
;
б)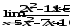 ;
;
в)
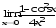 ;
г)
;
г)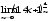 .
.
а)
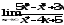 ;
б)
;
б)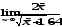 ;
;
в)
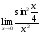 ;
г)
;
г)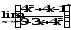 .
.
а)
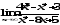 ;
б)
;
б)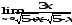 ;
;
в)
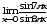 ;
г)
;
г)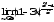 .
.
а)
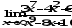 ;
б)
;
б)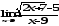 ;
;
в)
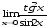 ;
г)
;
г)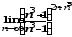 .
.
а)
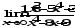 ;б)
;б)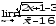 ;
;
в)
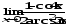 ;г)
;г)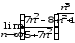 .
.
а)
 ;
б)
;
б)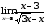 ;
;
в)
 ;
г)
;
г)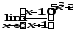 .
.
а)
 ;б)
;б)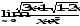 ;
;
в)
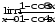 ;
г)
;
г)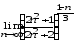 .
.
а)
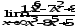 ;
б)
;
б)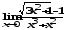 ;
;
в)
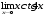 ;
г)
;
г)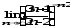 .
.
а)
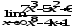 ;б)
;б)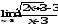 ;
;
в)
 ;
г)
;
г)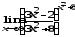 .
.
а)
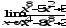 ;
б)
;
б)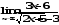 ;
;
в)
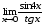 ;
г)
;
г)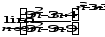 .
.
а)
 ;
б)
;
б)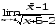 ;
;
в)
 ;
г)
;
г)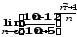 .
.В задачах 81-100 определить производные
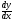 ,
пользуясь формулами дифференцирования.
,
пользуясь формулами дифференцирования.
а)
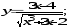 б)
б)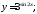 в)
в) г)
г)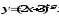
а)
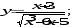 б)
б)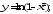 в)
в) г)
г)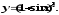
а)
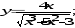 б)
б)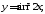 в)
в)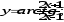 г)
г)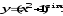
а)
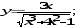 б)
б)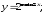
в)
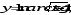 г)
г)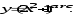
а)
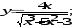 б)
б) в)
в)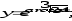 г)
г)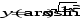
а)
 б)
б)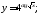 в)
в)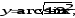 г)
г)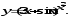
а)
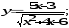 б)
б) в)
в) г)
г)
а)
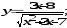 б)
б)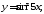 в)
в)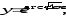 г)
г)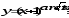
а)
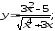 б)
б)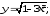 в)
в) г)
г)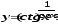
а)
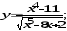 б)
б)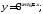 в)
в)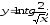 г)
г)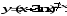
а)
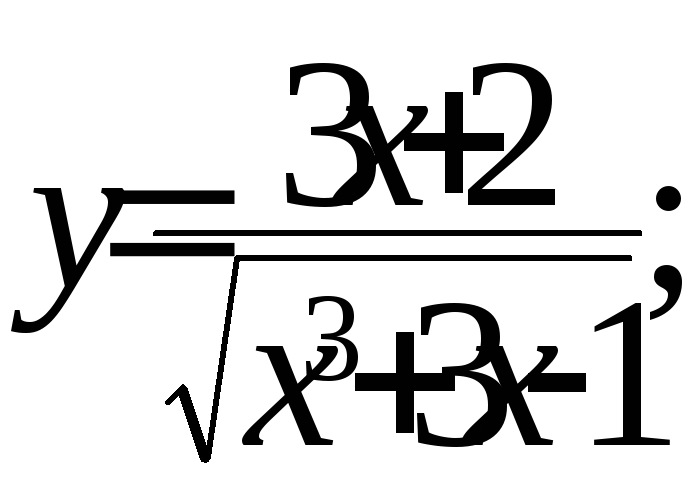 б)
б)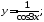 в)
в)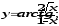 г)
г)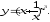
а)
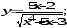 б)
б)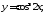 в)
в)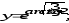 г)
г)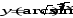
а)
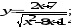 б)
б)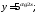 в)
в) г)
г)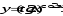
а)
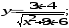 б)
б)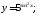 в)
в)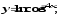 г)
г)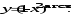
а)
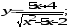 б)
б)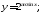 в)
в)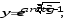 г)
г)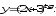
а)
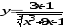 б)
б)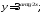 в)
в) г)
г)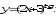
а)
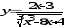 ;
б)
;
б)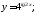 в)
в)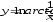 ;
г)
;
г)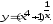
а)
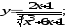 б)
б)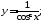 в)
в)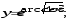 г)
г)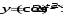
а)
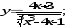 б)
б)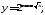 в)
в) г)
г)
а)
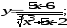 б)
б)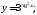 в)
в)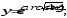 г)
г)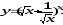
В задачах 101–120 найти интегралы:
а)
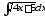 ;
б)
;
б)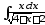 ;
в)
;
в)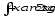 .
.а)
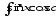 ;
б)
;
б)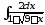 ;
в)
;
в)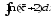 .
.а)
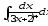 ;
б)
;
б)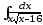 ;
в)
;
в)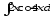 .
.а)
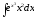 ;
б)
;
б)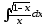 ;
в)
;
в)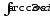 .
.а)
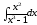 ;
б)
;
б)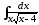 ;
в)
;
в)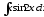 .
.а)
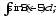 ;
б)
;
б)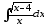 ;
в)
;
в)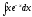 .
.а)
 ;
б)
;
б)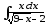 ;
в)
;
в)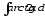 .
.а)
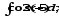 ;
б)
;
б)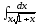 ;
в)
;
в)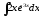 .
.а)
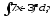 ;
б)
;
б)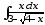 ;
в)
;
в)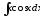 .
.а)
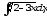 ;
б)
;
б) ;
в)
;
в)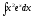 .
.а)
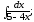 ;
б)
;
б)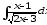 ;
в)
;
в)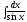 .
.а)
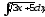 ;
б)
;
б)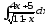 ;
в)
;
в)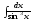 .
.а)
 ;
б)
;
б)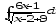 ;
в)
;
в)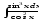 .
.а)
 ;
б)
;
б)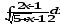 ;
в)
;
в)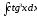 .
.а)
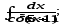 ;
б)
;
б)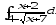 ;
в)
;
в)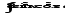 .
.а)
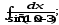 ;
б)
;
б)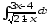 ;
в)
;
в)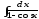 .
.а)
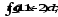 ;
б)
;
б)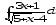 ;
в)
;
в)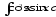 .
.а)
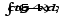 ;
б)
;
б) ;
в)
;
в)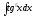 .
.а)
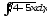 ;
б)
;
б)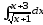 ;
в)
;
в)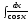 .
.а)
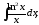 ;
б)
;
б)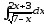 ;
в)
;
в)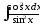 .
.
В задачах 121–140 вычислить определенные интегралы:
а)
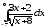 ;
б)
;
б)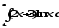 .
.а)
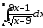 ;
б)
;
б)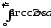 .
.а)
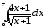 ;
б)
;
б)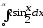 .
.а)
 ;
б)
;
б)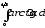 .
.а)
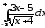 ;
б)
;
б)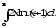 .
.а)
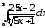 ;
б)
;
б)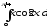 .
.а)
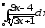 ;
б)
;
б) .
.а)
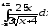 ;
б)
;
б)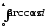 .
.а)
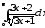 ;
б)
;
б)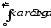 .
.а)
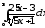 ;
б)
;
б)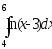 .
.а)
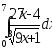 ;
б)
;
б)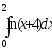 .
.а)
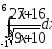 ;
б)
;
б)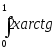 .
.а)
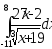 ;
б)
;
б) .
.а)
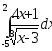 ;
б)
;
б)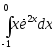 .
.а)
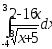 ;
б)
;
б)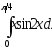 .
.а)
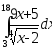 ;
б)
;
б)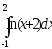 .
.а)
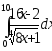 ;
б)
;
б)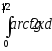 .
.а)
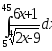 ;
б)
;
б)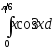 .
.а)
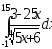 ;
б)
;
б)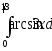 .
.а)
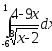 ;
б)
;
б)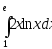 .
.
.Вычислить площадь фигуры, ограниченной параболами
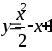 и
и
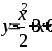
Вычислить площадь фигуры, ограниченной эллипсом
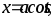
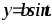
Вычислить площадь фигуры, ограниченной астроидой
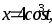
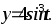
Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболой
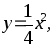 прямой
прямой
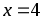 и осью Оx.
и осью Оx.Вычислить объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной гиперболой y=6/x,осью Оу и прямыми у = 1 и у = 6.
Вычислить объем тела, образованного вращением фигуры, ограниченной линиями
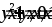 вокруг осиOY.
вокруг осиOY.Вычислить площадь фигуры, ограниченной линиями:
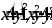 .
.Вычислить объем тела, образованного вращением фигуры, ограниченной линиями
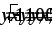 вокруг осиOY.
вокруг осиOY.Вычислить объем тела, образованного вращением фигуры, ограниченной линиями
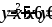 вокруг осиOX.
вокруг осиOX.
Вычислить объем тела, образованного вращением фигуры, ограниченной линиями
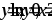 вокруг осиOY.
вокруг осиOY.Вычислить площадь фигуры, ограниченной линиями
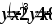 .
.Вычислить объем тела, образованного вращением фигуры, ограниченной линиями
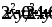 вокруг осиOX.
вокруг осиOX.Вычислить площадь фигуры, ограниченной линиями:
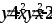 .
.Вычислить площадь фигуры, ограниченной линиями:
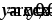 .
.Вычислить объем тела, образованного вращением фигуры, ограниченной линиями
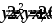 вокруг осиOX.
вокруг осиOX.Вычислить площадь фигуры, ограниченной линиями:
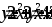 .
.Вычислить объем тела, образованного вращением фигуры, ограниченной линиями
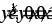 вокруг осиOX.
вокруг осиOX.Вычислить площадь фигуры, ограниченной линиями:
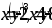 .
.
Вычислить площадь фигуры, ограниченной линиями:
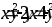 .
.Вычислить объем тела, образованного вращением фигуры, ограниченной линиями
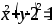 вокруг осиOX.
вокруг осиOX.
В задачах 161– 170 дана функция

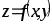 .
Записать:
.
Записать:1) полный дифференциал dz;
2) частные производные второго порядка
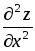
 и
и ;
;3) смешанные частные производные
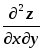 и
и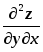 .
.
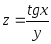 .
.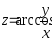
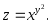
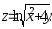
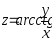
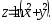
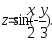
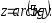
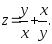
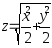 .
.Дана функция
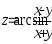 .
Показать, что
.
Показать, что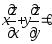
Дана функция
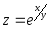 .
Показать, что
.
Показать, что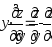 .
.Дана функция
 .
Показать, что
.
Показать, что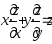
Дана функция
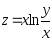 .
Показать, что
.
Показать, что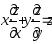 .
.Дана функция
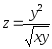 .
Показать, что
.
Показать, что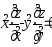 .
.Дана функция
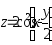 .
Показать, что
.
Показать, что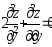 .
.Дана функция
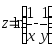 .
Показать, что
.
Показать, что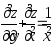 .
.Дана функция
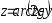 .
Показать, что
.
Показать, что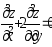 .
.
Дана функция
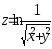 .
Показать, что
.
Показать, что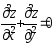 .
.Дана функция
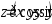 .
Показать, что
.
Показать, что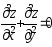 .
.
В задачах 181–200 требуется: 1) построить на плоскости хОу область интегрирования заданного интеграла; 2) изменить порядок интегрирования и вычислить площадь области при заданном и измененном порядках интегрирования.
В задачах 201-210 исследовать сходимость рядов, пользуясь признаком сходимости Даламбера.
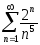 .
.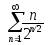 .
.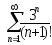 .
.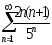 .
.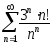 .
.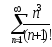 .
.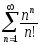 .
. .
. .
.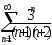
В задачах 211-220 исследовать сходимость рядов, пользуясь интегральным признаком сходимости Коши.
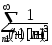 .
.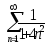 .
.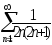 .
.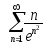 .
. .
. .
.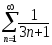 .
.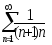 .
. .
.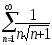
В задачах 221–230 найти общее решение (общий интеграл) дифференциальных уравнений первого порядка.
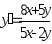 .
.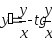 .
.
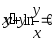 .
.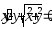
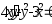 .
.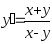 .
.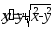 .
.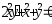 .
.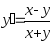 .
.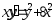
В задачах 231–240 указать частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям.
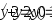 .
.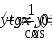 .
.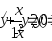 .
. ,
,
 .
.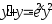 ,
,
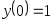 .
.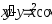 ,
,
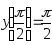 .
.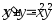 ,
,
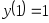 .
.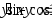 ,
,
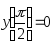 .
.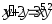 ,
,
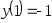 .
.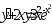 ,
,
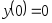 .
.
В задачах 241 – 260 даны линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Записать частное решение, удовлетворяющее указанным начальным условиям.
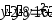 ,
,
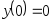 ,
,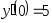 .
.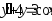 ,
,
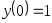 ,
,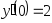 .
.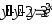 ,
,
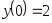 ,
,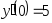 .
.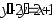 ,
,
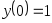 ,
,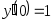 .
.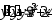 ,
,
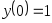 ,
,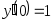 .
.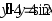 ,
,
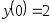 ,
,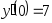 .
.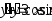 ,
,
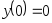 ,
, .
.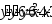 ,
,
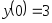 ,
,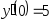 .
.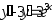 ,
,
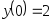 ,
,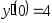 .
.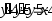 ,
,
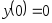 ,
,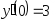 .
.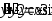 ,
,
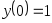 ,
,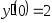 .
.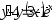 ,
,
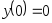 ,
,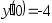 .
.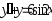 ,
,
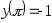 ,
,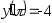 .
.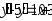 ,
,
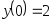 ,
,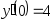 .
.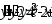 ,
,
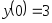 ,
,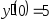 .
.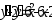 ,
,
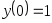 ,
,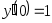 .
.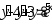 ,
,
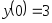 ,
,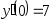 .
.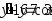 ,
,
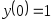 ,
,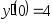 .
.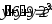 ,
,
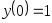 ,
, .
.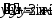 ,
,
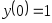 ,
,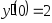 .
.
В ящике лежат 10 белых и 5 красных шаров, одинаковых на ощупь. Вынули наугад 5 шаров. Какова вероятность того, что из вынутых шаров не менее трех белых?
Группа туристов из 15 юношей и 5 девушек выбирают хозяйственную команду в составе четырёх человек. Какова вероятность того, что в составе этой команды окажутся два юноши?
Студент выучил 40 из 60 вопросов. Какова вероятность того, что он сдаст экзамен, если для этого необходимо ответить не менее чем на два из трех вопросов билета?
В ящике имеется 12 однотипных деталей, среди которых четыре нестандартные. Извлечены 3 детали. Какова вероятность того, что среди них не более одной нестандартной?
Из 20 акционерных обществ пять являются банкротами. Некто приобрел по одной акции семи АО. Какова вероятность того, что среди купленных три окажутся акциями банкротов?
В ящике 15 деталей, среди которых 10 окрашенных. Сборщик извлекает пять деталей. Какова вероятность того, что две детали окажутся окрашенными?
В ящике лежат 10 белых и 5 красных шаров, одинаковых на ощупь. Вынули наугад 6 шаров. Какова вероятность того, что четыре из них белые?
В группе студентов 10 юношей и 7 девушек. Какова вероятность того, что в подгруппе, выбранной наудачу из шести человек, окажутся 2 девушки?
Из 40 вопросов, входящих в экзаменационные билеты, студент выучил 30. Какова вероятность того, что среди трех вопросов билета, студент знает не более одного?
В партии из 20 изделий четыре имеют скрытый дефект. Какова вероятность того, что из пяти взятых изделий два являются дефектными?
Среди 50 деталей 20 первого сорта. Какова вероятность того, что из пяти взятых деталей две окажутся первого сорта?
В студенческой группе 15 девушек и 10 юношей. На консультацию случайным образом приглашаются семь человек. Какова вероятность того, что среди приглашенных будет пять юношей?
Району выделили 10 комбайнов, причем 7 из них изготовлены на Красноярском заводе. Определить вероятность того, что среди пяти наудачу взятых комбайнов три изготовлены в Красноярске.
Группа туристов из 15 юношей и 5 девушек выбирают хозяйственную команду в составе четырех человек. Какова вероятность того, что в составе этой команды окажутся не менее трёх юношей?
Студент выучил 30 из 60 вопросов. Какова вероятность того, что он сдаст экзамен, если для этого необходимо ответить не менее чем на два из трех вопросов билета?
В ящике имеется 12 однотипных деталей, среди которых четыре нестандартные. Извлечено 5 деталей. Какова вероятность того, что среди них не более двух нестандартных?
В студенческой группе 7 девушек и 10 юношей. Для дежурства случайным образом приглашаются семь человек. Какова вероятность того, что среди приглашенных будет не менее пяти юношей?
Из колоды в 36 карт наугад вынимаются пять карт. Какова вероятность того, что среди взятых карт окажутся три туза?
Группа туристов из 5 юношей и 15 девушек выбирают хозяйственную команду в составе четырёх человек. Какова вероятность того, что в составе этой команды окажутся два юноши?
Студент выучил 20 из 60 вопросов. Какова вероятность того, что он сдаст экзамен, если для этого необходимо ответить не менее чем на два из трех вопросов билета?
В задачах 281-290 использовать формулу Бернулли для определения вероятностей появления события при повторении испытаний.
Всхожесть семян некоторого сорта пшеницы составляет 85%. Найти вероятность того, что из пяти посеянных семян взойдут: а) три; б) не менее трех.
В хлопке число длинных волокон составляет 80%. Какова вероятность того, что среди взятых наудачу 6 волокон длинных окажется: а) четыре; б) не более двух.
Принимая вероятность рождения мальчика равной 0,51, найти вероятность того, что среди 5 новорожденных: а) 4 мальчика; б) не более двух девочек.
В некотором водоеме караси составляют 80%.Найти вероятность того, что из 5 выловленных в этом водоеме рыб окажется: а) 3 карася; б) не менее 4 карасей.
Прибор состоит из 3 узлов. Вероятность безотказной работы в течение смены для каждого узла равна 0,8. Узлы выходят из строя независимо один от другого. Найти вероятность того, что за смену откажут: а) два узла; б) не менее двух узлов; в) все узлы.
Вратарь парирует в среднем 0,3 всех одиннадцатиметровых штрафных ударов. Какова вероятность того, что он возьмет: а) три из пяти мячей; б) не менее четырёх мячей?
Всхожесть семян ржи составляет 90%. Чему равна вероятность того, что из восьми посеянных семян взойдут: а) три; б) не менее шести.
Для данного баскетболиста вероятность забросить мяч в корзину равна 0,7. Произведено восемь бросков. Что вероятнее: он забросит мяч в корзину четыре или шесть раз?
В магазин вошли шесть покупателей. Определить вероятность того, что: а) три из них совершат покупки; б) не более двух совершат покупки. Вероятность совершить покупку для каждого покупателя равна 0,3
Вероятность выигрыша по облигации займа равна 0,25. Какова вероятность того, что из восьми облигаций: а) три выиграют; б) не менее семи выиграют?
В задачах 291—300 использовать асимптотическую формулу Пуассона для определения вероятностей появления события при повторении испытаний.
Семена содержат 0,15% сорняков. Какова вероятность при случайном отборе 2000 семян обнаружить 6 семян сорняков?
Вероятность появления бракованной детали равна 0,006. Найти вероятность того, что из 500 случайно отобранных деталей окажется: а) 5 бракованных; б) хотя бы одна бракованная.
Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение часа равна 0,002. Определить вероятность того, что за час откажут: а) 4 элемента; б) хотя бы один элемент.
Вероятность выживания бактерий после радиоактивного облучения равна 0,004. Найти вероятность того, что после облучения из 500 бактерий останется не более 2 бактерий.
Книга издана тиражом в 100000 экземпляров. Вероятность того, что в книге имеется дефект брошюровки равна 0,0001. Определить вероятность того, что тираж содержит: а) 5 неправильно сброшюрованных книг; б) хотя бы одну неправильно сброшюрованную книгу.
Вероятность госпитализации пациента при эпидемии гриппа равна 0,002. Определить вероятность того, что из 1000 заболевших, поликлиника направит на госпитализацию только шесть пациентов.
Вероятность того, что изделие не выдержит испытания, равна 0,006. Какова вероятность того, что из 600 проверяемых изделий не выдержат испытания только три?
При передаче сообщения вероятность искажения одного знака равна 0,02. Определить вероятность того, что сообщение из 100 знаков содержит ровно три искажения.
К пульту охранной сигнализации предприятия подключено 2000 датчиков, причем вероятность появления тревожного сигнала на каждом из них равна 0,0005. Определить вероятность тревоги (для чего достаточно хотя бы одного сигнала)
При массовом производстве элементов электроники вероятность брака равна 0,005. Определить вероятность того, что в партии из 800 элементов бракованными будут три элемента.
Вероятность того, что после одного учебного года учебник уже нельзя будет использовать в дальнейшем, равна 0,25. Определить вероятность того, что придется закупить не менее 85 и не более 105 новых учебников, чтобы к новому учебному году в библиотеке ВУЗа их снова было 400. Определить наивероятнейшее число учебников требующих замены и вероятность наивероятнейшего числа таких учебников.
Упаковщик укладывает 900 деталей, проверенных ОТК или изготовленных рабочими, имеющими личное клеймо. Вероятность того, что деталь помечена личным клеймом, равна 0,1. Определите вероятность того, что среди них окажется с личным клеймом: а) 115деталей; б) от 100 до 120 деталей.
В жилом доме имеется 5000 ламп, вероятность включения каждой из них в вечернее время равна 0,8. Определить вероятность того, что число одновременно включенных ламп будет от 2300 до 2700. Определить наивероятнейшее число включенных ламп и вероятность наивероятнейшего числа включенных ламп.
К магистральному водопроводу подключены 180 предприятий, каждое из которых с вероятностью 0,6 в данный момент времени осуществляет отбор воды. Определить вероятность того, что в данный момент времени забор воды производят не менее 90 и не более 120 предприятий. Определить наивероятнейшее число и вероятность наивероятнейшего числа предприятий, производящих в данный момент времени забор воды.
Телефонный кабель состоит из 400 жил. С какой вероятностью этим кабелем можно подключить к телефонной сети 390 абонентов, если для подключения каждого абонента нужна одна жила, а вероятность того, что она повреждена, равна 0,0125. Определите наивероятнейшее число подключенных к сети абонентов. Какова вероятность того, что будут подключены от 320 до 360 абонентов.
В первый класс школы должны принять 200 детей. Вероятность рождения мальчика равна 0,515. Определить: а) наивероятнейшее число мальчиков среди первоклассников; б) вероятность того, что среди первоклассников мальчиков и девочек будет поровну; в) что мальчиков будет от 120 до 170.
При штамповке металлических клемм получается в среднем 90% стандартных. Определите: а) наивероятнейшее число и вероятность наивероятнейшего числа стандартных клемм в партии из 900 клемм; б) вероятность наличия от 790 до 820 годных клемм в этой партии.
Вероятность неточной сборки сеялки равна 0,1. Определить вероятность того, что среди 50 сеялок окажется от 30 до 45 точно собранных. Определить наивероятнейшее число и вероятность наивероятнейшего числа «точно» собранных сеялок.
Вероятность получения с конвейера изделия первого сорта равна 0,9. Определите вероятность того, что из взятых на проверку 600 изделий будут от 500 до 550 первого сорта. Определите наивероятнейшее число и вероятность наивероятнейшего числа изделий первого сорта.
Имеется 100 станков одинаковой мощности, работающих независимо друг от друга в одинаковом режиме, при котором их привод оказывается включенным в течение 0,8 всего рабочего времени. Какова вероятность того, что в произвольный момент времени окажутся включенными от 70 до 86 станков? Определите наивероятнейшее число и вероятность наивероятнейшего числа включенных станков.
Вероятность вызревания кукурузного стебля с тремя початками равна 0,7. Определите наивероятнейшее число таких стеблей и вероятность наивероятнейшего числа стеблей с тремя початками на опытном поле среди 500 стеблей. Определите вероятность того, что таких стеблей будет от 320 до 360.
Вероятность выхода из строя образца за время испытания на надежность равна 0,1. Какова вероятность того, что за это время из 100 образцов выйдут из строя от 9 до 28. Определите наивероятнейшее число и вероятность наивероятнейшего числа, вышедших из строя образцов.
Было высажено 400 деревьев, причем вероятность того, что дерево приживётся, для каждого из них равна 0,8. Какова вероятность того, что число прижившихся деревьев: а) ровно 260; б) от 350 до 400? Определите наивероятнейшее число прижившихся деревьев.
При посадке картофеля машиной СН-4Б в почву попадает 90% неповрежденных клубней. Какова вероятность того, что из 900 клубней будут не повреждены от 810 до 840 клубней? Определить наивероятнейшее число и вероятность наивероятнейшего числа неповрежденных клубней.
Гидравлическая система автомобиля насчитывает около 100 клапанов. Надежность каждого клапана равна 0,9. Какова вероятность отказа: а) трех клапанов; б) от семи до одиннадцати клапанов? Определить наивероятнейшее число отказавших клапанов.
Вероятность того, что после одного учебного года учебник уже нельзя будет использовать в дальнейшем, равна 0,35. Определить вероятность того, что придется закупить не более 95 новых учебников, чтобы к новому учебному году в библиотеке ВУЗа их снова было 400. Определить наивероятнейшее число учебников требующих замены и вероятность наивероятнейшего числа таких учебников.
В жилом доме имеется 4500 ламп, вероятность включения каждой из них в вечернее время равна 0,8. Определить вероятность того, что число одновременно включенных ламп будет от 2700 до 3200. Определить наивероятнейшее число включенных ламп и вероятность наивероятнейшего числа включенных ламп.
К магистральному водопроводу подключены 200 предприятий, каждое из которых с вероятностью 0,8 в данный момент времени осуществляет отбор воды. Определить вероятность того, что в данный момент времени забор воды производят не менее 130 и не более 180 предприятий. Определить наивероятнейшее число и вероятность наивероятнейшего числа предприятий, производящих в данный момент времени забор воды.
Упаковщик укладывает 900 деталей, проверенных ОТК или изготовленных рабочими, имеющими личное клеймо. Вероятность того, что деталь помечена личным клеймом, равна 0,1. Определите вероятность того, что среди них окажется: а) 85; б) от 80 до 110 деталей с личным клеймом. Определите наивероятнейшее число деталей с личным клеймом среди всех деталей.
По результатам проверок налоговыми инспекциями установлено, что в среднем каждое второе малое предприятие региона имеет нарушение финансовой дисциплины. Какова вероятность того, что из 1000 зарегистрированных в регионе малых предприятий имеют нарушения финансовой дисциплины: а) 320предприятий; б) от 480 до 520?
В задачах 321–340 задан закон распределения случайной величины X (в первой строке таблицы даны возможные значения величины X, а во второй строке указаны вероятности р этих возможных значений).
Вычислить: 1) математическое ожидание М(Х); 2) дисперсию D(Х); 3) среднее квадратическое отклонение σ.
25
30
35
40
45
0,2
0,3
0,2
0,1
0,2
5
10
15
20
25
0,1
0,3
0,4
0,1
0,1
5
15
25
35
45
0,1
0,1
0,3
0,3
0,2
3
8
13
18
23
0,2
0,2
0,3
0,2
0,1
2
3
4
5
6
0,1
0,2
0,4
0,2
0,1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
110
120
130
140
150
0,2
0,3
0,3
0,1
0,1
-10
0
10
20
30
0,1
0,2
0,3
0,3
0,1
10
12
14
16
18
0,1
0,1
0,6
0,1
0,1
8
11
14
17
20
0,2
0,1
0,3
0,3
0,1
25
30
35
40
45
0,2
0,3
0,2
0,1
0,2
14
16
18
20
0,1
0,2
0,3
0,4
24
26
28
30
0,2
0,3
0,1
0,4
12
16
18
26
0,2
0,3
0,1
0,4
27
28
34
36
0,2
0,2
0,1
0,5
21
25
29
34
0,1
0,4
0,1
0,4
32
36
38
42
0,1
0,3
0,2
0,4
14
16
25
30
0,2
0,2
0,2
0,4
54
66
68
70
0,2
0,3
0,1
0,4
|
|
|
|
|
|
|
|
|
|
|
|