
ТеорМЕХ3куПМ
.pdf1
А.И.СНОПОВ
ОСНОВЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
(СЕМ ЕСТРОВЫЙ КУРС ЛЕКЦИЙ)
Основные понятия, постулаты и допущения математического моделирования механических систем
Изменение положения тела в пространстве, происходяще е во времени, называют механическим движением, При математическом моделировании механических систем используются следующие понятия материальных тел
1. Материальная точка
Если при изучении движения тела можно пренебречь его размерами, то такое тело называют материальной точкой. Материальная точка может обладать бесконечно большой, конечной, бесконечно малой или нулевой массой.
Примеры: Солнце, планеты и кометы при моделировании движения солнечной системы нередко принимают за материальные точки. Однако при изучении движения муравья необходимо учитывать наличие у него ножек, головы и брюшка и здесь не всегда приемлемо моделирование муравья материальной точкой.
2. Механическая система
Множество материальных точек, положение и движение каждой из которых зависит от положения и движения остальных точек этого множества, называется механической системой. Механическая система может состоять из одной материальной точки, конечного или бесконечного их числа.
3. Абсолютно твердое тело
Механическая система, в которой расстояния между всеми материальными точками, ее образующими, остаются неизменными при равновесии или движении под действием любой системы сил, называется абсолютно твердым телом.
Математическое моделирование механической системы включает в себя:
-определение понятий пространства и времени, -способы математического описания положения механической системы в пространстве и
времени, - математические понятия скорости и ускорения как основных характеристик движущейся
материальной точки,
-математические понятия сил, действующих на механическую систему, и характеристик соответствующих силовых полей,
-понятие массы материальной точки.
-способы составления дифференциальных уравнений, описывающих движение механических систем,
-способы извлечения информации о движении механических систем из этих
дифференциальных уравнений и их реализация для конкретных механических систем, В предлагаемом курсе лекций последний пункт рассматриваются очень кратко, так как объем
курса мал и нет возможности его иллюстрировать примерами по извлечению информации из системы дифференциальных уравнений, описывающих движение механических систем.
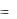
2
Способы извлечения такой информации для конкретных механических систем содержатся в курсах дифференциальных и интегральных уравнений, математической физики и многочисленных спецкурсах по различным разделам механики систем и сплошных сред.
В основе математического моделирования механических систем лежат понятия, постулаты и допущения, сформулированные Исааком Ньютоном (1643-1727г.г.) в его знаменитой книге "Математические начала натуральной философии” (1687 г.), в которой изложены постулаты:
а) существования абсолютного пространство
Существует абсолютное пространство, свойства которого не зависят от материи, его заполняющей, оно обладает свойствами абсолютно твердого тела, однако абсолютно проницаемое для всех тел, в нем находящихся, неподвижное, безграничное, трехмерное. имеет меру длины.
б) существования абсолютного времени
Абсолютное время равномерно течет в абсолютном пространстве и не зависит от положения и скорости наблюдателя. Все события происходят в определенной последовательности времени.
Все события происходят во времени и пространстве. Для их изучения надо ввести систему координат (для простоты – ортогональную декартову), жестко связанную с абсолютным пространством. Для отсчета абсолютного времени надо ввести начало отсчета времени.
Основываясь на наблюдениях и введенных понятиях, Ньютон сформулировал четыре постулата (законы Нью тона), имеющие место для абсолютных пространства и времени, которые входят в основу математического моделирования механических систем
1.(Закон инерции) Всякое тело (подразумевается – материальная точка) продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения (состояние инерционного движения), пока и поскольку оно не понуждается приложенными силами изменить это состояние.
Из этого постулата следует
а) существование бесконечного множества абсолютных пространств, которые совершают непрерывные движения друг относительно друга с постоянными скоростями (галилеевые системы отсчета),
б) определение понятие силы, как причины, нарушающей инерционное движение мате6риальной точки
2.( Второй закон Ньютона) Производная по времени от количества движения материальной точки пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует
d |
|
|
|
|
||
|
|
|
|
|
||
(mv |
) F |
(1.1) |
||||
dt |
||||||
|
|
|
|
|
||
где mv - количество движения материальной точки (векторная величина)
3
F- сила, действующая на материальную точку, m - масса материальной точки,
v- скорость точки (векторная величина).
При постоянной массе материальной точки второй закон Ньютона, если учесть, что
|
|
|
|
|
|
|
|
|
|
|
|
|||||
производная по времени от скорости точки есть ускорение точки ( |
dv |
|
|
w ), |
можно записать так |
|||||||||||
dt |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
(1.2) |
|
|||||
|
|
mw |
F |
|
|
|||||||||||
3. |
(Закон действия и противодействия) Действию |
|||||||||||||||
|
всегда |
есть |
равное |
и |
противоположное |
|||||||||||
|
противодействие, иначе, взаимодействия двух тел |
|||||||||||||||
А |
(подразумеваетсяматериальных точек) друг на друга |
|||||||||||||||
между |
собой |
|
равны |
и |
направлены |
в |
||||||||||
|
|
|||||||||||||||
В |
противоположные сторон |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
(1.3) |
|
|||||
|
|
F А |
|
FВ |
|
|
||||||||||
Рис.1.1
4. Закон параллелограмма сил) Действие двух сил, приложенных к одной материальной точке, эквивалентно действию одной силы, приложенной к этой же точке и равной
векторной сумме этих сил
F 2 |
F F1 |
F2 |
(1.4) |
|
М
F
F1
Рис.1/2
Цели и разделы курса
Чтобы выразить законы Ньютона в математической форме необходимо ввести математические понятия скорости и ускорения материальной точки, количества движения материальной точки, массы материальной точки, силы, действующей на материальную точку, а также понятия покоя и траектории материальной точки.
Понятия траектории, скорости и ускорения материальной точки определяются в разделе курса, именуемом “кинематика”.
Свойства сил и операций с силами изучаются в разделе “статика”.
Только после введения и соединения этих понятий излагается основное содержание курса –
создание математических моделей описания движения механических систем под влиянием сил, на них действующих, что составляет содержание раздела “динамика”.
В случае, когда механическая система состоит из одной материальной точки, силы, действующие на нее, могут быть заменены одной эквивален тной силой, которая в процессе движения может менять свое направление и величину и в общем случае являться векторной функцией координат этой точки, скоростей их изменения и времени, Как будет в курсе показано, ускорение материальной точки вычисляется по формуле

|
|
|
|
4 |
|||
|
|
|
d 2 |
|
|
|
|
|
|
w |
r |
||||
|
|
dt |
2 |
|
|
||
|
|
|
|
||||
где |
векторная координата точкиt. |
|
|
|
|
|
|
r |
|
|
|
|
|
||
Векторное уравнение 2-го закона Ньютона принимает вид
m d |
2 |
F( x ,x ,x ,x |
,x |
,x ,t ) |
||||
r |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
1 |
2 |
3 |
|
dt2 |
|||||||
|
|
|
|
|
|
|
||
Проецирование этого уравнения на координатные оси, приводит к системе трех скалярных обыкновенных дифференциальных уравнений второго порядка которую для краткости записи можно представить так :
d 2 x |
1 |
Fi ( x1 , x2 , x3 , x1 , x2 , x3 ,t ), mi m,i 1,2,3 |
|
i |
|
|
|
dt2 |
|
m |
|
|
|
i |
|
Если же имеется механическая система, состоящая из N материальных точек, то на каждую из них, в общем случае, будет действовать система сил, обусловленная действием тел, не включенных в систему, и тел, образующих систему. И эти силы могут зависеть от координат всех точек системы, их производных по времени и времени. Не все из этих сил бывают известными функциями координат и времени. Система сведется к 3N обыкновенным дифференциальным уравнениям второго порядка
|
d 2 x |
1 |
Fi ( x1 , x2 , x3 , x1 , x2 , x3 ,...,x3N |
2 , x3n 1 , x3N , x3 N 2 , x3n 1 , x3N ,t ), i 1,2,...3N |
|
|
i |
|
|
||
|
dt2 |
|
m |
||
|
|
|
i |
|
|
для составления которых надо установить вид правых частей. |
|||||
Если учесть, что среди тел, образующих механическую систему, могут быть не абсолютно твердые тела типа сплошных сред, состоящие из бесконечного числа материальных частиц,, то N  , и получение такой системы уравнений, во многом теряет смысл. Исключением являются абсолютно твердые тела, движение которых может быть описано конечным числом дифференциальных уравнений.
, и получение такой системы уравнений, во многом теряет смысл. Исключением являются абсолютно твердые тела, движение которых может быть описано конечным числом дифференциальных уравнений.
В предлагаемом ниже курсе лекций ограничиваемся изложением только основ математического моделирования механических систем, состоящих из конечного числа материальных точек и абсолютно твердых тел.
Основы математического моделирования механических систем, составляющие содержание предлагаемого курса лекций, включают в себя
- введение понятий о системах отсчета и о способах определения положения материальных точек и абсолютно твердых тел в этих системах отсчета,
-введения понятий, характеризующих быстроту изменения положения и характера движения материальных точек и абсолютно твердых тел в различных системах отсчета,
-введение понятий о механических системах и о связях, налагаемых на них,
-введение понятий сил и операций с ними,
-разработка способов применения законов Ньютона к описанию движения механических систем,
-установление общих теорем динамики механических систем,
-установление уравнений движения механических систем на основе вариационных
принципов динамики систем,
5
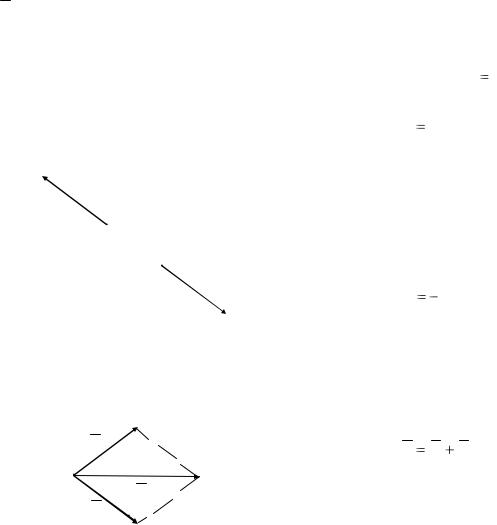
КИНЕМАТИКА Описание движения материальной точки
Для приложения законов Ньютона к материальной точке надо уметь описывать ее
положение в пространстве в каждый момент |
времени., |
Здесь необходимо учесть, что в |
условиях Земли, или других планет, а также |
в условиях управляемых объектов (машина, |
|
самолет, корабль, космическая станция и |
т.п.) неудобно пользоваться неподвижными |
|
системами координат. Изучение движения приходится проводить в подвижных, и не
обязательно декартовых, |
системах координат. Например, |
наблюдение за |
космическими |
|||||||
|
|
|
|
объектами с вращающейся Земли проводится в |
||||||
|
|
|
|
сферических координатах. Поэтому одной из |
||||||
|
|
|
|
важных задач |
математического |
моделирования |
||||
|
|
|
|
движения механических систем является задача |
||||||
|
|
O |
|
описания движения механических |
систем в |
|||||
|
|
|
подвижных системах координат, |
в том числе не |
||||||
|
|
M |
|
|||||||
x3 |
|
|
являющихся декартовыми. |
|
|
|
|
|
||
|
(t) |
|
|
|
|
|
||||
r |
dr |
Векторный способ описания |
движения |
|||||||
|
|
|
|
материальной точки. |
|
|
|
|
|
|
|
|
|
|
Выбирается некоторая система координат, |
||||||
|
|
|
x 2 |
например, декартовая x,y,z,O, |
|
|
положение |
|||
x1 |
|
материальной точки в которой определяется |
||||||||
|
|
|
|
векторным уравнением движения |
|
|
|
|
|
|
Рис. |
|
|
|
|
|
|
|
(t) |
||
|
|
|
r |
r |
||||||
|
|
|
|
из которого следует скалярная запись уравнений |
||||||
|
|
|
|
движения, определяющих закон движения |
||||||
|
|
|
|
материальной точки по траектории |
|
|
|
|||
|
|
|
x |
x(t) |
|
|
|
|
|
|
|
|
|
y |
y(t) |
|
|
|
|
|
|
z z(t)
Уравнения () одновременно определяют в параметрической форме вид траектории. Скорость движущейся материальной точки определяется вектором
|
|
|
|
|
|
|
v |
dr |
|
|
r |
(x, y, z) |
|
|
|
|
|
|||
dt |
|
|||||
|
|
|
|
|
||
Проекции скорости на координатные оси вычисляются по формулам
vx |
dx |
x |
, |
|||
|
||||||
dt |
||||||
|
|
|
|
|
||
vy |
dy |
y |
, |
|||
|
||||||
dt |
||||||
|
|
|
|
|
||
vz |
|
dz |
z |
|
|
|
|
|
|
|
|||
|
dt |
|
|
|||
|
|
|
|
|
||
Ускорение движущейся материальной точки в выбранной системе определяется вектором
|
dv |
|
d 2 |
|
|
|
|
|
|
r |
|
|
|||
w |
dt |
|
dt2 |
|
v |
r (x, y, z) |
|
|
|
|
|
|
|||
Проекции ускорения на координатные оси вычисляются по формулам

|
|
|
|
|
|
6 |
|
|
|
||
|
dv |
vx |
d 2 x |
x, |
|||||||
wx |
|
x |
|
|
|
|
|
|
|||
|
dt |
dt2 |
|||||||||
|
|
|
|
||||||||
wy |
|
dvy |
vy |
|
|
d 2 y |
y , |
||||
|
dt |
|
|
dt2 |
|||||||
|
|
|
|
|
|
||||||
|
|
dv |
vz |
|
d 2 z |
z |
|||||
wz |
|
z |
|
|
|
|
|
|
|||
|
dt |
|
dt2 |
||||||||
|
|
|
|
|
|||||||
Естественный способ описания движения материальной точки
1)задается траектория движения материальной точки в прстранстве,
2)задается начальная точка О на траектории,
3)задается положительная область на траектории, определяемая направлением единичного
вектора касательной к ней в начальной точке О,
4) положение материальной точки на траектории определяется длиной дуги s траектории, соединяющей начальную точку О с положением материальной точки на траектории в заданный момент времени. Если дуга лежит в положительной области траектории, то принимается s 0 ,
а в отрицательной – s 0
5) задается закон движения материальной точки по траектории
s = s(t)
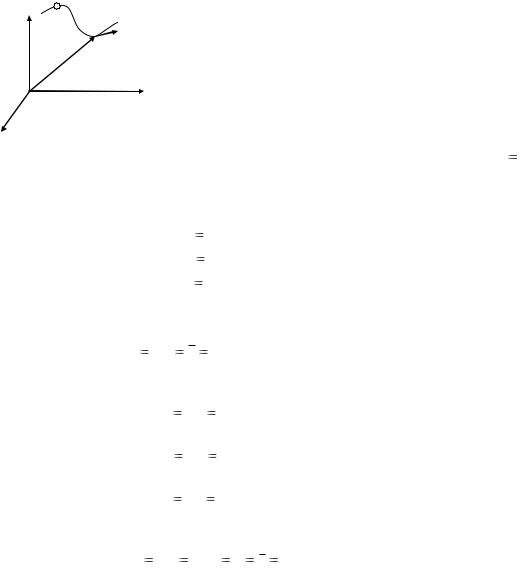
Скорость
Исходя из определения понятия скорости, можем записать
|
|
|
|
|
|
v |
dr |
|
v |
|
|
|
|
|
τ |
||
dt |
|
||||
|
|
|
|
||
так как вектор скорости направлен по касательной к траектории в текущей точке.. Если учесть, что
dr ds
то можем записать
|
|
|
|
|
|
|
|
|
v |
dr |
|
|
ds |
|
|
v |
|
|
|
|
|
|
|
|
||
dt |
|
|
dt |
|||||
|
|
|
|
|
|
|||
Сравнивая () и (), получаем
vds dt
Ускорение
Исходя из определения понятия ускорения, можем записать
|
dv |
|
d 2 |
|
|
w |
r |
|
|||
dt |
|
dt2 |
|
||
|
|
|
|||
В проекциях на декартовы оси имеем

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
||||
w |
dv |
d |
|
(v |
|
) |
|
|
dv |
|
|
v |
d |
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
dt |
dt |
|
|
|
|
|
dt |
|
dt |
|||||||||||||||
В общем случае величины |
v |
|
и |
|
|
|
|
|
могут изменяться со временем. Учитывая (), имеем |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
dv |
|
|
d |
ds |
|
d 2s |
w |
||||||||||||||||
|
|
|
|
|
|
( |
|
) |
|
|
|||||||||||||||
|
|
dt |
dt |
dt |
|
dt2 |
|||||||||||||||||||
Так как - единичный вектор, то имеет место равенство
2 1
из которого следует
|
|
d ( |
2 |
) |
2 |
|
d |
|
0 |
|
|||||
|
|
|
|
|
|
|
|
||||||||
|
Возможны два случая: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
d |
0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
d |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В первом случае имеет место равенство |
|
|||||||||||||
|
|
|
w |
w |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
в той точке траектории, где находится ее точка перегиба.. |
|
||||||||||||||
|
Во втором случае, как следует из формулы (), |
|
|||||||||||||
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
и согласно теории пространственных кривых, излагаемой в |
дифференциальной геометрии, |
||||||||||||||
можно записать |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
d |
|
|
|
|
|
d |
|
n |
() |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где n - единичный вектор главной нормали к траектории ( лежит в соприкасающейся плоскости кривой, которая получается в пределе из плоскости, проходящей через три точки кривой, одна из которых точка М , а остальные расположены по бокам от нее, и стремятся к ней).
Введем в рассмотрение также единичный |
вектор b (бинормаль), |
который ортогонален к |
||||
векторам |
|
|
чтобы тройка векторов |
|
|
|
|
и n , причем направляемего так, |
|
, n , |
b , построенных в |
||
точке М кривой, определяла правую систему координат (называемую естественным трехгранником). Деля обе части равенства () на dt , получаем равенство
d |
|
d |
|
|
|
|
n |
dt |
|
dt |
8
Из векторного треугольника (рис. ) следует равенство
d d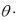 1
1
из которого следует
d d
d
что позволяет записать равенство () так
|
|
|
|
|
|
|
d |
|
|
d |
|
|
ds |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
dt |
|
|
ds |
|
|
dt |
|
|
|
|
|
|
|
||||||||
|
|
' |
|
d |
|
Принимая во внимание формулу (), |
имеем |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
d |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
n |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
||||||||||||
|
M |
|
|
|
|
|
dt |
|
|
|
|
|
|
|||||||||||||||
|
Рис. |
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. |
|
|
|
|
В теории пространственных кривых доказывается, что |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
d |
|
|
|
d |
|
|
|
ds |
1 |
|
v |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
vn |
|
n |
|||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
ds |
dt |
ds |
R |
|||||||||||||
d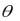
M |
где R – радиус кривизны траектории в данной точке. |
|
Рис.
|
w |
|
где w |
|
|
|
dv |
|
|
|
v2 |
||
w |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|||
|
|
dt |
|
R |
||||
|
|
|
|
|
||||
|
касател ьное ускорение |
центрострем ител ьноеускорение |
||||||
Эту формулу обычно пишут в таком виде
|
|
|
w |
w |
wn |
 - касательное ускорение
- касательное ускорение
Рис.
|
v2 |
|
|
wn |
|
n |
- центростремительное |
|
|||
|
R |
|
|
ускорение
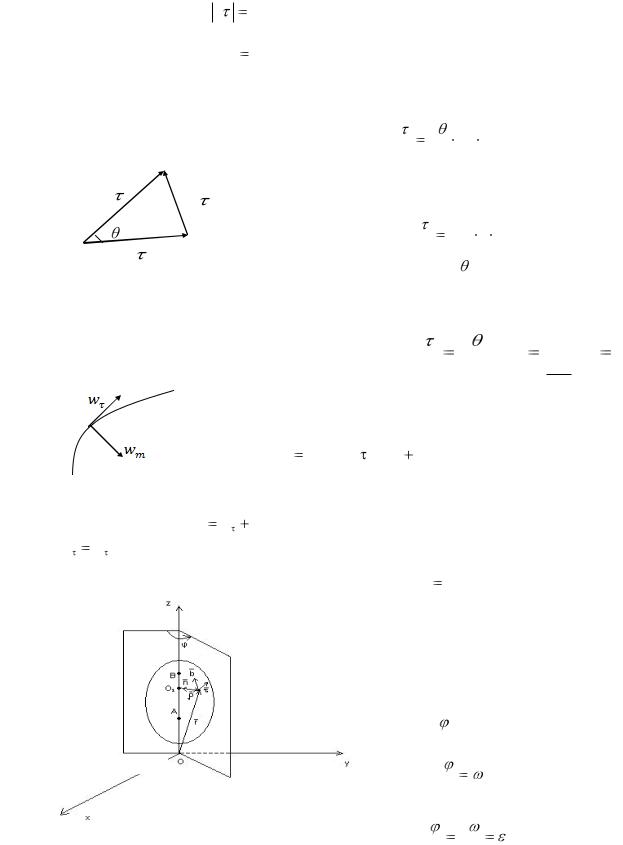
Вращательное движение абсолютно твердого тела.
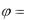 (t) - закон вращательного движения.
(t) - закон вращательного движения.
|
|
d |
- |
угловая скорость |
|||
|
|
|
|
||||
|
|
dt |
|||||
|
|
|
|
|
|
||
вращения твѐрдого тела. |
|||||||
|
d 2 |
|
|
d |
|
- угловое ускорение. |
|
|
dt2 |
|
dt |
||||
|
|
|
|||||

9
Введем вектор угловой скорости:
z 0
и вектор углового ускорения
d |
|
|
|
|
z 0 |
|
|
|
|
||
|
|
|
|
|
|
dt |
|
||||
|
|
|
|
||
Представим радиус-вектор точки М тела в виде суммы двух взаимно ортогональных векторов
|
|
|
|
|
|
|
|
|
|
|
z 0 , |
|
|
|
|
|
|
|
OO |
1 |
|
, OO1 |
OO |
|
OO1 |
||||||
|
|
|
|
|
|||||||||||
|
r |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим траекторию точки М тела, являющуюся окружностью, радиус которой
const,
Свяжем с точкой М и окружностью |
|
|
|
|
|
|
const оси естественного трехгранника. |
|||||||||||||
|
|
|
|
|
|
|||||||||||||||
При этом имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OO1 |
|
n |
|
|
|
|||||||
r |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Тск как OO1 const и |
|
const, то скорость точки М равна |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dn |
|
||
|
|
|
|
|
|
|
|
|
v |
|
dr |
|||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
dt |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Для координатных единичных векторов естественного трехгранника имеет место соотношение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
b |
|
|
|||||||||||||
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Откуда следует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
dn |
|
db |
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
b |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
dt |
|
dt |
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
dt |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Вектор |
b по построению единичный вектор |
|
|
|
параллельный оси Oz Поэтому можно принять |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
b z0 |
и записать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dn |
|
|
|
z0 |
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
С учетом этого равенства формула для скорости точки вра щающегося тела принимает вид |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
v |
dr |
|
|
|
|
|
|
z0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
dt |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Единичный вектор 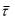 перпендикулярен подвижной плоскости, в которой расположена точка М тела и его направление зависит только от угла положения этой подвижной плоскости . Поэтому можно записать
перпендикулярен подвижной плоскости, в которой расположена точка М тела и его направление зависит только от угла положения этой подвижной плоскости . Поэтому можно записать
.
Так как , согласно формуле () ,
d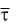 d d
d d d
d
dt d dt d
d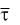 d
d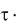 n и d
n и d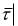
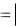 d , то
d , то
d |
|
|
n |
|
|
||
|
|
|
|
d |
|
|
|
|
|
|
то

10
|
|
|
|
|
|
d |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и формула ( ) принимает вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
dr |
|
|
z |
0 |
|
|
|
n |
|
|
|
z0 ( n ) |
|||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Учитываем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Формула () принимает вид |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Если принять во внимание, что |
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
OO1 |
|
и OO1 || |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
||||||||||||
То из формулы ( ) будет следовать равенство |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|||||
именуемое формулой Эйлера, определяющей распределение скоростей точек твердого тела при его вращении вокруг неподвижной оси
Движение тела с одной неподвижной точкой (сферическое движение).
Тело с одной неподвижной точкой никогда не может совершать поступательного движения, так как при поступательном движении скорости всех точек тела одинаковые. Неподви жная точка тела всегда имеет нулевую скорость. Поэтому для движущегося тела .с одной неподвижной точкой единственный вариант возможного поступательного движения - мгновенный покой. В остальные моменты времени тело должно участвовать в общем случае в мгновенных вращательных движениях. Поэтому в любой момент времени в теле найдется еще хотя бы одна точка, имеющая нулевую скорость При этом а вектор мгновенной угловой скорости тела должен лежать на линии проходящей через неподвижные точки тела,
определяющие положение мгновенной оси вращения тела. |
Вектор угловой скорости |
|||||||
|
|
|
|
( t ) |
( t ) |
|
0( t ) определяет положение оси вращения и величину угловой скорости. |
|
|
|
|
|
|||||
Ось мгновенного вращения в сферическом движении меняет свое положение и описывает некоторые конические поверхности в неподвижном пространстве и пространстве, жестко связанном с телом.
Формула Эйлера () определяет в любой момент времени распределение скоростей в теле и для
случаев, когда тело имеет одну неподвижную точку.
v 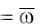 r
r
Дифференцирование по времени можно определить распределение ускорений в теле, имеющем одну неподвижную точку
|
dv |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
||||
w |
|
|
|
|
|
|
r |
|
|
|
|
|
|
dt |
|
dt |
|
|
|
|
dt |
|
|||||
|
|
|
|
|
|
|
|
|
|||||
d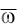
Величина dt определяет вектор мгновенного углового ускорения тела с одной
неподвижной точкой
