
ТеорМЕХ3куПМ
.pdf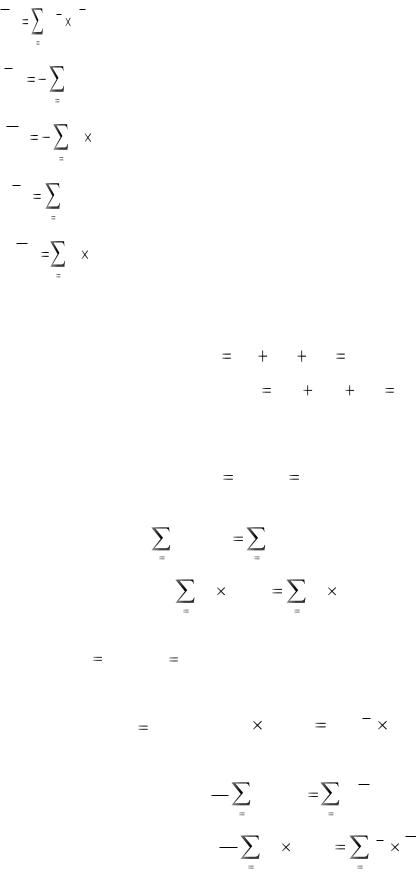
31
n
М е
О
k 1
R i n
О
М i n
О
R i
О
М i
О
rk F |
е |
|
k |
- главный момент всех внешних сил, действующих на систему. |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mk wk |
- главный вектор сил инерции системы. |
||||||
k |
1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
mk wk |
|
|
|
rk |
- главный момент сил инерции системы. |
|||||||||
k |
1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
i |
|
|
- главный вектор внутренних сил системы |
||||
|
|
|
|
|
|
k |
|
|
|||
k 1 |
|
|
|
|
|||||||
n |
|
|
|
|
|||||||
|
|
|
|
|
|
|
F |
i |
|
||
|
r |
- главный момент внутренних сил системы |
|||||||||
|
|
|
|
k |
|
|
k |
||||
k |
1 |
|
|
|
|
|
|
|
|
|
|
Главный вектор и главный момент всей системы сил, приложенных к механической системе (включая силы инерции), также должны быть равными нулю, так как система этих сил по принципу Даламбера находящейся равновесии.. Поэтому должны выполняться равенства
R |
R |
е |
R |
i n |
R |
i |
0 |
|
|
||||||
О |
|
|
О |
|
|
О |
|
|
О |
|
|
|
|||
|
|
|
|
|
|
е |
|
|
i n |
|
|
i 0 |
|||
|
М |
о |
|
М |
|
М |
|
М |
|||||||
|
|
|
|
|
|
|
О |
|
|
|
О |
|
|
О |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Согласно же третьего закона Ньютона внутренние силы в системе попарно уравновешены, и поэтому вся система внутренних сил является уравновешенной. Вследствие этого должны быть равными нулю главный вектор и главный момент внутренних сил
|
|
|
|
|
|
|
|
|
|
|
|
i |
0, |
|
i |
|
|
|
|
|
|
|||
|
|
|
|
|
R |
М |
0 . |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
О |
|
|
|
О |
|
|
|
|
|
|
||
С учетом сказанного из уравнений () следуют равенства |
||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|||
|
|
|
|
|
|
m w |
|
|
|
|
F |
е , |
|
|
||||||||||
|
|
|
|
|
|
|
|
k |
|
|
k |
|
|
|
|
k |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
k |
|
1 |
|
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
m w |
|
|
|
|
F |
е |
||||||
|
|
|
|
|
r |
|
r |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
k |
k |
|
|
k |
k |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
||||||
|
|
dvk |
|
|
|
|
|
|
|
|
||||||||||||||
Так как |
w |
, v |
|
|
drk |
, |
а массы всех материальных точек системы принимаются |
|||||||||||||||||
|
k |
|
|
|
|
|
|
|||||||||||||||||
|
k |
dt |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
неизменными, то справедливы равенства
|
d |
|
|
|
|
|
|
m w |
(m v |
) |
r |
||||
|
|||||||
k k |
dt |
k k |
|
|
k |
||
|
|
|
|
|
|
||
что позволяет уравнения () записать так d n
dt k 1 d n
dt k 1
mk wk |
|
d |
||
|
|
|||
|
dt |
|||
|
|
|
|
|
|
|
|
n |
|
mk vk |
|
|
||
|
|
|
k 1 |
|
|
|
|
||
rk mk vk |
||||
(rk mk vk )
F е ,
k
n
rk Fkе
k 1

|
|
|
|
|
32 |
||
Введем обозначения |
|||||||
|
|
|
|
n |
|
|
|
|
Q |
|
mk vk - количество движения механической системы, |
||||
|
|
|
|
k |
1 |
|
|
|
|
|
|
n |
|||
GО |
|
|
|
||||
rk mk vk - момент количества движения механической системы относительно |
|||||||
|
|
|
|
k |
1 |
|
|
точки О (кинетический момент механической системы относительно точки О). |
|||||||
Теорема о количестве движения:
Согласно введенным обозначениям уравнение () записывается так
|
|
|
n |
|
|
dQ |
|
||||
|
F е |
||||
|
|
|
|||
dt |
|
||||
|
|
k |
|||
|
k 1 |
||||
что позволяет сформулировать теорему:
Производная по времени от количества движения системы равна суме всех внешних сил, действующих на систему.
Следствие
Теорема о движении центра масс
Количество движения системы можно представить так
|
|
|
d |
n |
|
|
|
Q |
|
|
mk |
|
|
||
|
|
|
rk |
||||
|
dt k |
||||||
|
|
|
1 |
|
|
||
Используем понятие центра масс системы, введенное формулой ().
n
mk rk М rС
k 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
При этом количество движения системы |
|
Q выражается через массу системы и скорость ее |
||||||||||||||||||||||
центра масс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 |
|
|
|
|||
|
|
|
|
|
|
|
|
dr |
|
|
dQ |
|
r |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Q |
|
|
( М rС |
) М |
|
|
|
C |
МvC , |
|
М |
|
C |
МwC |
||||||||||
|
dt |
|
dt |
dt |
dt2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
а уравнение ( ) принимает вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
d 2 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
F е |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
М |
|
|
C |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
dt2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
k 1 |
|
|
k |
|
|
|
|
|
|
|||||||
Получили теорему о движении центра масс
Центр масс системы движется как материальная точка, обладающая массой, равной массе всей системы, на которую действуют все внешние силы, приложенные к системе.
Замечание. Если внешние силы не зависят от внутренних сил системы, то уравнения движения центра масс системы можно интегрировать независимо от уравнений движения системы.
Например, движение Солнечной системы в астрономии рассматривается на основе модели, исключающей влияние на Солнечную систему сил, действующих на нее со стороны остальных
тел Вселенной (звезд, галактик и т.п. ) в |
связи |
с их большой удаленностью. Поэтому |
||
n |
|
|
|
|
принимается, что для Солнечной системы |
|
F |
е |
0 . Это дает основание считать чно центр |
|
|
k |
|
|
k |
1 |
|
|
|
масс Солнечной системы движется инерционно с постоянной скоростью. Так как планеты и другие тела Солнечной системы обладают суммарно пренебрежимо малой массой по сравнению с массой Солнца, то центр масс Солнечной системы практически совпадает с центром Солнца, который движется в ближнем космосе прямолинейно и с постоянной скоростью. в дальнем космосе Солнце участвует во вращательном движении вокруг центра нашей галактики –

33
Млечного пути .с периодом обращения в миллиарды световых лет. На протяжении миллионов лет Ту дугу этой траектории которую центр Солнца проходит за миллионы лет с большой точностью ожно аппроксимировать прямой линией. Солнце движется относительно местного стандарта покоя со скоростью 19,4 км/с в направлении точки на небесной сфере с координатами  (эта точка наз. апексом).
(эта точка наз. апексом).
Теорема о моменте количества движения (о кинетическом моменте)
Согласно введенным обозначениям уравнение () записывается так
|
|
|
n |
|
|
||
dGО |
|
|
|||||
|
|
|
F |
е |
|||
r |
|||||||
dt |
|
k |
k |
||||
k 1 |
|||||||
|
|
|
|
|
|
||
что позволяет сформулировать теорему:
Производная по времени от момента количества движения системы равна суме моментов всех внешних сил, действующих на систему.
Эта теорема имеет исключительно важное значение для исследования вращательных
движений тел |
(колес, роторов моторов и турбин различного назначения, искусственных и |
|||||||||||||||||||||||||||||||||||||||||
естественных небесных тел и. т.д. и т.п.). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Теорема о кинетической энергии. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Кинетическая энергия системы вычисляется по формуле |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
1 n |
m |
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 k 1 |
|
|
|
k |
k |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теорема Кенига |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Положим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vC |
|
vk , |
|
|
|
|||||||||||||||
rk |
rC |
rk , При этом имеем vk |
|
|
|
|
||||||||||||||||||||||||||||||||||||
где |
|
k - скорость относительного движения материальной точки вокруг центра масс. |
||||||||||||||||||||||||||||||||||||||||
v |
||||||||||||||||||||||||||||||||||||||||||
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
v 2 |
|
v 2 |
2v |
|
v |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
C |
|
k |
|
|
|
C |
|
k |
|
|
|
|
|
|
|
|||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
1 |
|
|
n |
|
|
|
2 |
|
|
|
|
2 |
n |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
T |
|
|
Mv |
|
|
|
|
|
|
|
|
|
m v |
|
|
|
|
v |
|
|
|
m v |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
2 k 1 |
|
|
k |
|
C |
k 1 |
k |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Здесь последнее слагаемое равно нулю в силу следующих равенств |
||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
dr |
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
m v |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
r |
|
|
|
|
|
|
( Mr |
) 0 , так как |
r 0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
k |
k |
k 1 |
|
k |
|
|
dt |
|
|
|
dt |
|
|
k |
|
k |
|
|
|
|
dt |
|
|
|
C |
|
C |
|||||||||||
|
|
k 1 |
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Поэтому имеем математическое содержание теоремы Кенига |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
1 |
Mv 2 |
|
|
|
1 |
|
|
n |
m v 2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
C |
|
|
|
2 k 1 |
|
k |
|
k |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Кинетическая энергия системы материальных точек равна сумме кинетической энергии центра масс системы , как материальной точки, в которой сосредоточена вся масса системы, и кинетической энергии системы в ее относительном движении вокруг центра масс.
Теорема о кинетической энергии
При движении системы ее кинетическая энергия может изменять свою величину. Для установления величины этого изменения обращаемся к уравнениям движения системы (), в которых систему сил разбиваем на системы внешних и внутренних сил.
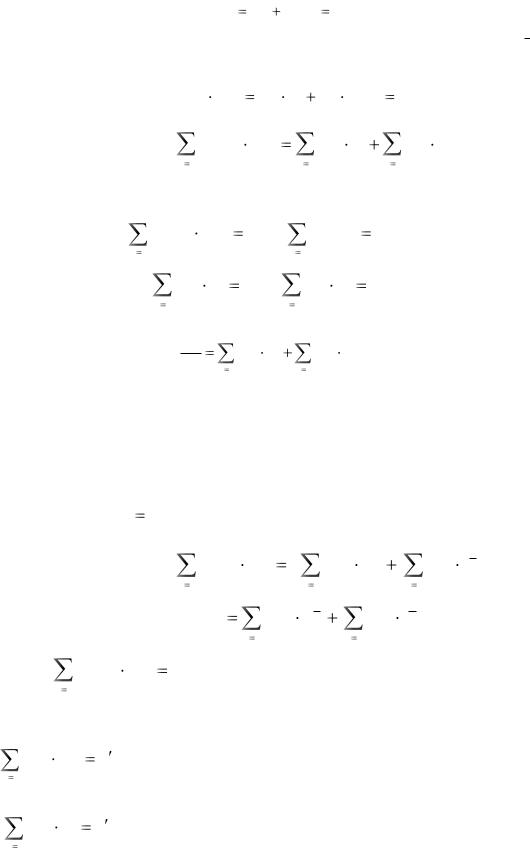
|
|
|
|
|
|
34 |
|||
|
|
dvk |
|
|
|
i k 1, 2,...,n |
|||
m |
k |
|
F |
e |
|
F |
|||
dt |
|||||||||
|
|
k |
|
k |
|||||
Умножим сначала скалярно обе части уравнения () на вектор скорости vk и просуммируем полученные равенства. Получим
|
|
|
dvk |
|
|
|
|
e |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||
m v |
k |
|
F |
|
v |
k |
F |
|
v |
k |
k |
1,2,...,n |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
k |
|
dt |
|
|
|
k |
|
|
|
|
k |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n |
|
|
|
|
dvk |
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|||
|
|
m v |
|
|
|
|
|
F |
e v |
|
|
F |
i v |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
k |
1 |
|
kv k |
|
dt |
|
k |
1 |
|
|
|
k |
|
k |
k |
1 |
k |
k |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Известно, что произведение силы на скорость определяет мощностью силы, для обозначения которой используется символ N . Используем обозначения
n |
|
|
dv |
|
d |
|
1 |
|
n |
|
|
|
|
dT |
|
|||
m v |
|
|
k |
|
|
( |
|
|
|
m v 2 |
) |
|
|
, |
||||
|
|
|
|
|
|
|
|
|
||||||||||
kv k |
|
|
dt |
|
dt |
|
2 k 1 |
k |
k |
|
|
dt |
|
|||||
k 1 |
|
|
|
|
|
|
|
|
||||||||||
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
F |
e v |
N e , |
|
|
|
F |
i v |
|
N i , |
|
|||||||
|
|
k |
k |
|
|
|
|
|
|
k |
|
k |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
k 1 |
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
||
Уравнение () принимает вид
dT
dt
n |
|
n |
|
||||
|
F |
e v |
|
F |
e v |
||
|
k |
k |
|
k |
k |
||
|
|
|
|
||||
k 1 |
|
k 1 |
|
||||
из которого следует такая формулировка теоремы о кинетической энергии системы.
Производная по времени от кинетической энергии механической системы равна сумме мощностей всех сил, как внешних, так и внутренних, действующих на систему.
Умножаем скалярно каждое |
уравнение на элементарное перемещение |
|
|
|
drk |
||||
соответствующей материальной точки, |
совершаемое ею за промежуток времени dt , |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
учитываем, что |
drk |
|
vk , |
а полученные уравнения суммируем. |
|
.Получаем |
||||||||||||||||||||||||
dt |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m v |
dv |
|
F |
е |
|
|
|
|
|
|
F |
i dr |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k k |
k |
|
k |
|
|
k |
|
k |
k |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
k 1 |
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
||
Или |
|
|
|
|
|
|
|
|
|
|
dT |
|
F |
е drk |
|
|
|
|
|
F |
i drk |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
k |
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
так как |
|
|
|
|
mkv vk |
dvk |
dT - приращение кинетической энергии системы |
|||||||||||||||||||||||
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
за бесконечно малый промежуток времени dt . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
F |
е |
|
|
|
|
d Ае - работа всех внешних сил, действующих на систему, на |
|||||||||||||||||||||||
|
drk |
|||||||||||||||||||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
элементарных перемещениях: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
F |
i |
|
|
|
d Аi |
|
|
|||||||||||||||||||||
|
|
drk |
|
- работа всех внутренних сил, действующих на систему, на |
||||||||||||||||||||||||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
элементарных перемещениях:

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обратим внимание на то, что дифференциальное выражение |
F |
|
|
|
d А |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
drk |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
может не быть полным дифференциалом, поэтому дифференциал работы |
d А помечен |
|||||||||||||||||||||||||||||||||||||||||||
штрихом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
Получили теорему о кинетической энергии в дифференциальной форме |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
Приращение |
кинетической энергии |
механической |
системы |
за |
бесконечно малый |
|||||||||||||||||||||||||||||||||||
промежуток времени равно сумме элементарных работ всех внешних |
и внутренних сил, |
|||||||||||||||||||||||||||||||||||||||||||
действовавших на систему в этот промежуток времени, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
За конечный промежуток времени |
t1 t0 каждая точка системы совершает конечные |
|||||||||||||||||||||||||||||||||||||||
перемещения. из положения, |
определяемого координатами |
|
|
|
0 , в положение с координатами |
|||||||||||||||||||||||||||||||||||||||
r |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
1 , а |
|
силы, |
действующие на |
нее, |
совершали |
|
работу, величина |
которой |
равна значению |
|||||||||||||||||||||||||||||||||
r |
|
|||||||||||||||||||||||||||||||||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
криволинейного интеграла (интегрирование ведется вдоль траектории точки) |
|
|||||||||||||||||||||||||||||||||||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если T0 |
- начальное значение кинетической энергии системы, |
а T1 |
- конечное, то после |
||||||||||||||||||||||||||||||||||||
интегрирования уравнения () получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
1 |
|
|
|
|
|
|
n |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е dr |
|
|
|
F i dr |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
T |
|
|
|
k |
F |
|
|
|
|
|
|
k |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
0 |
|
k |
|
k |
|
|
|
|
|
0 |
|
k |
k |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rk |
|
|
|
|
|
|
rk |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
n |
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F е |
|
|
|
|
Ае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
k |
dr |
|
- работа всех внешних сил, перемещавших систему из начального положения |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
rk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в конечное; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
n |
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F i |
|
|
|
|
Аi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
k |
dr |
|
- |
работа |
всех |
|
внутренних |
сил, |
|
перемещавших систему из начального |
||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
rk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
положения в конечное.
Получили теорему об изменении кинетической энергии в конечной форме
Приращение кинетической энергии механической системы за конечный промежуток времени равно сумме работ всех внешних и внутренних сил, перемещавших эту систему в этот промежуток времени.
Замечание. Подынтегральные выражения в формуле () могут не быть полными дифференциалами, Поэтому численные значения работ Аk могут зависеть от форм траекторий
материальных точек. Как будет показано ниже, в случаях, когда силы потенциальные, работа, производимая ими, не зависит от форм траекторий, соединяющих начальые и конечные их точки.
Теорема о кинетической энергии имеет важное значение для развитии техники ((энергетика, транспорт, освоение космоса и.т.д.).
Потенциальные силы
Для упрощения дальнейшего изложения теории изменим обозначения некоторых величин. Обозначениям координат точек
х1 , y1 ,z1 ,х2 , y2 ,z2 , ..., хN , yN ,zN , |
Х k dхk Yk dyk Zk dzk |
ставим в соответствие новые обозначения координат
х1, х2 , х3 , х4 , х5 , х6 , ..., х3N 2 , х3N 1, х3N
Обозначениям проекций сил

36
Х1,Y1, Z1, Х 2 ,Y2 , Z2 ,..., Х N ,YN , ZN ,
ставим в соответствие новые обозначения проекций сил
Х1, Х 2 , Х 3 , Х 4 , Х 5 , Х 6 , ..., Х 3N 2 , Х 3N 1, Х 3N
Обозначениям масс
m1, m1, m1, m2 , m2 , m2 , ..., mN , mN , mN ,
ставим в соответствие новые обозначения масс
m1, m2 , m3 , m4 , m5 , m6 , ..., m2 N 2 , m3N 1, m3N ,
В новых обозначениях формула () записывается так
3N |
|
3N |
|
|
dT |
Х е dх |
Х i dх |
||
|
k |
k |
k |
k |
|
|
|
||
k |
1 |
|
k 1 |
|
Потенциал сил
Если можно найти такую функцию |
U е ( х ,х |
2 |
,...,х |
), что имеют место равенства |
|||
|
|
|
|
1 |
3 N |
|
|
Х е |
U |
е |
|
|
|
|
|
|
|
,k 1,,2,...,3N |
|
||||
|
|
|
|||||
k |
хk , |
|
|
|
|
||
|
|
|
|
|
|
|
|
то говорят, что внешние силы потенциальные, а функцию U е называют потенциалом внешних сил, действующих на систему.
Если же существует такая функция U i ( х1, х2 ,..., х3N ) , что выполнчются равенства
|
|
|
Х i |
U i |
|
, k |
1,,2,...,3N |
|
|
|
|
хk , |
|||||
|
|
|
k |
|
|
|
||
то говорят, что |
внутренние силы потенциальные, |
а функция U i называется потенциалом |
||||||
внутренних сил системы. |
|
|
|
|
|
|
||
Если существует такая функция U i ( х , х ,..., х |
) , что имеют место равенства |
|||||||
|
|
|
|
1 |
2 |
3N |
|
|
|
|
|
Х i |
U i |
|
, k |
1,,2,...,3N |
|
|
|
|
хk , |
|||||
|
|
|
k |
|
|
|
||
то функция U i ( х , х ,..., х |
) называется потенциалом внутренних сил системы |
|||||||
1 |
2 |
3N |
|
|
|
|
|
|
Если внешнее и внутреннее силовые поля потенциальные, то можно ввести в рассмотрение
функцию U |
U е |
U i , называемую потенциалом всех сил, действующих на систему. |
||||||||||||||||
|
|
|
|
|
Потенциальная энергия |
|
|
|
|
|
|
|||||||
Функцию |
|
V |
|
U называют |
потенциальной |
энергией всей системы сил, |
||||||||||||
действующих на механическую систему. |
|
|
|
|
|
|
|
|||||||||||
Функцию |
|
V е |
|
U е |
называют потенциальной энергией поля внешних сил. |
|||||||||||||
Функцию |
V i |
|
U i |
называют потенциальной энергией поля внутренних сил. |
||||||||||||||
|
|
|
|
|
|
|
Интеграл энергии |
|
|
|
|
|
|
|||||
Если внутренние и внешние силы потенциальные, то имеют место равенства |
||||||||||||||||||
|
3 N |
Х |
е dх |
|
3 N |
U е |
|
dх |
|
dU е , |
3N |
Х i dх |
3 N |
U i |
dх |
|
dU i |
|
|
|
k |
|
|
хk , |
|
k |
|
k |
хk , |
k |
|||||||
|
|
|
k |
|
|
|
|
|
|
k |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
k 1 |
|
|
|
k 1 |
|
|
|
|
k 1 |
|
k 1 |
|
|
|
||||
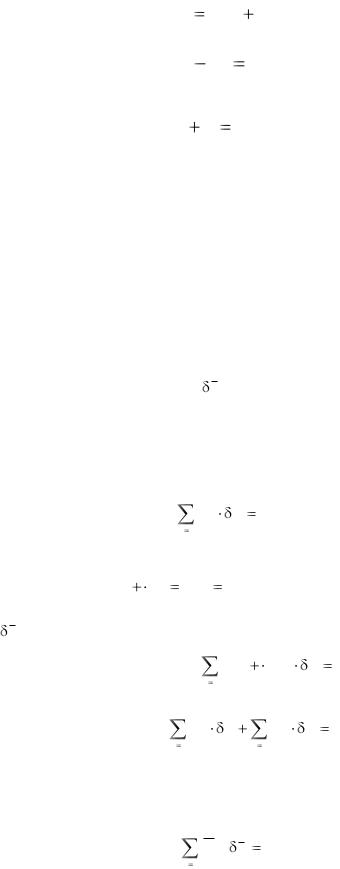
37
Равенство () принимает вид
dT dU е U i )
которое можно записать так
d(T U) 0
Следовательно, при движении механической системы в поле потенциальных сил, на нее действующих, выполняется закон сохранения полной механической энергии этой системы
T V const
Вариационные основы моделирования динамики механических систем Принцип возможных перемещений Лагранжа (1736-1813)
В 1788 г. Лагранж опубликовал книгу «Аналитическая механика», в которой изложил вариационный принцип, получивший его имя, который позволил значительно проще изучать равновесие механических систем с идеальными связями, пользуясь понятием виртуальной работы.
Лагранж разделяет силы, действующие на систему, на два типа: |
активные силы |
Fka и |
||
|
|
|
|
|
реакции связей N k . |
|
|
||
Рассматриваются идеальные (без трения) и к тому же |
не освобождающие |
|||
(двусторонние) связи. |
|
|
||
Вводятся понятия виртуальных (возможных) перемещений системы. тоесть таких бесконечно малых перемещений rk , совместимых со связями, которые допускаются для
системы точек в фиксированный момент времени.
Принцип возможных перемещений Лагранжа формулируется так Если на механическую систему наложены только идеальные не освобождающие связи, то для
равновесия системы необходимо и достаточно, чтобы сумма работ на возможных перемещениях всех активных сил, действующих на систему, равнялась нулю.
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
Fka |
|
|
0 |
|
|
|
|
|
|
|
r |
||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
k 1 |
|
|
|
||
Для установления основ |
этого принципа обратимся к условиям равновесия системы сил, |
|||||||||
действующих на покоящиеся материальные точки системы |
||||||||||
|
|
|
|
|
|
|
||||
Fka Nk |
0, k |
1,,2,...,N |
||||||||
Умножим каждое из равенств на соответствующее возможное перемещение материальной точки rk и суммируем полученные равенства по всем k . Получим
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
Fka |
N k ) |
|
|
|
|
0 |
||||||
|
|
|
r |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
N |
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
||
|
Fka |
|
|
|
|
N k |
|
|
0 |
||||||||
|
r |
|
r |
||||||||||||||
|
|
|
|
k |
|
|
|
|
|
|
k |
|
|||||
k 1 |
|
|
|
|
|
k 1 |
|
|
|
|
|
||||||
Идеальные связи представляют собой некоторые поверхности, для которых реакции связей ортогональны к этим поверхностям и поэтому возможные перемещения обязательно расположены в касательных плоскостях к этим поверхностям. Поэтому идеальные связи работы не производят и для них имеют место равенства
N
N k  rk 0
rk 0
k 1
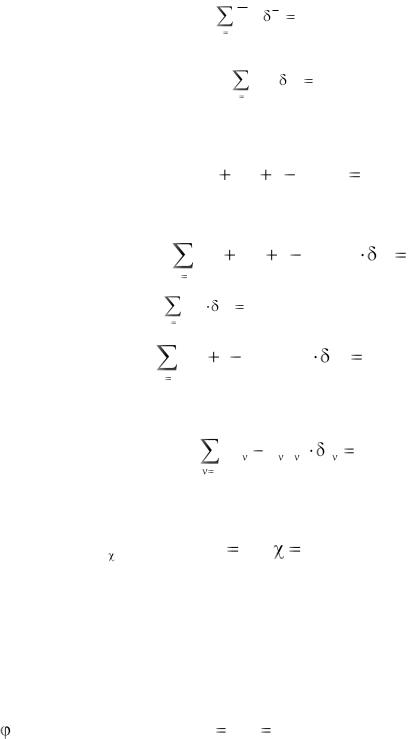
38
Эти равенства можно принимать за определение идеальных связей. В силу сказанного имеем
N
Fka  rk 0
rk 0
k 1
или
3N
X ka  xk 0
xk 0
k 1
Принцип ДаламбераЛагранжа. Общее уравнение динамики.
По принципу Даламбера в каждый момент времени
|
|
|
|
Fk |
Nk |
( mk wk |
) 0 |
Умножаем каждое уравнение на виртуальное перемещение соответствующей материальной точки и суммируем
|
N |
|
|
|
|
|
|
|
|
|
|||
|
|
|
[Fk |
Nk |
( mk wk |
)] |
rk |
0 |
|||||
|
k 1 |
|
|
|
|
|
|
|
|
|
|||
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
Для идеальных связей |
N k |
|
|
|
0 и |
уравнение принимает вид: |
|||||||
rk |
|||||||||||||
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Fk |
( mk wk )] |
rk |
|
0 |
|
|||||||
k1
-принцип Даламбера – Лагранжа. а само уравнение называется общим уравнением механики. В
скалярной форме
3N(X m x ) x 0
1
Типы связей. Уравнения связей.
1. Геометрические (голономные) связи
f ( x1 ,...,x3 N ,t ) 0, |
1,...,k |
Если время явно не входит в |
уравнение связи, то связь называют стационарной |
(склерономной). |
|
. Нестационарные связи иначе называют реономными.
2. Неголономные связи
ρ (x1 ,x2 ,...,x3N ,x1 ,x2 ,...,x3N ,t) 0, ρ 1,2,...,r - неголономные связи, если только они не
интегрируемые.
2а. Наиболее простые и часто встречающиеся - линейные неголономные связи

|
|
39 |
|
||
3 N |
|
|
|
|
|
a |
x a |
0; 1,2,...,r |
|||
1 |
|
|
|
|
|
a ,a |
| x,t |
x |
dx |
||
|
|
||||
dt |
|||||
|
|
|
|||
Связи накладывают ограничения на положения материальных точек, на скорости, на действительные элементарные перемещения и на виртуальные перемещения точек системы.
Рассмотрим сначала ограничения, налагаемые связями на действительные перемещения
1.Голономные связи налагают ограничения, согласно которым материальные точки остаются на связях и после перемещений. Следовательно, справедливы равенства
|
|
|
|
|
f |
( x1 ,...,x3 N ,t |
) |
0, |
|
1,...,k |
|||||||
где |
штрихом |
помчены |
|
|
координаты |
точек |
|
системы в момент времени |
|||||||||
t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полагаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
t |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
dx |
ν |
1,...3, N |
|||||
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( x1 |
dx1 ,...,x3 N |
|
dx3 N ,t |
|
dt ) |
|
0, |
|
1,...,k |
|||||||
Производя линеаризацию функции по малым приращениям ее аргументов, получаем |
|||||||||||||||||
|
|
|
|
3N |
f |
|
|
|
|
f |
|
|
|
|
|
||
|
f ( x1 ,...,x3N ,t ) |
|
|
|
|
dx |
|
dt, 0, |
1,...,k |
||||||||
|
|
1 |
|
x |
|
|
t |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как |
f χ (x1 ,...,x3N ,t) |
0 при |
|
χ |
1,...,k |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
то имеют место равенства, определяющие усдловия, |
налагаемые голономными связями на |
||||||||||||||||
действительные перемещения точек за промежуток времени dt. |
|||||||||||||||||
|
|
3N |
f |
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
dt, 0, |
|
1,...,k |
||||||||
|
|
1 |
|
x |
|
|
t |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Линейные неголономные связи налагают на перемещения точек сис=темы такие связи, непосредственно следующие из уравнений связей, если каждое из них умножить на dt.
3N |
|
a dx a dt 0; |
1,2,...,r |
1 |
|
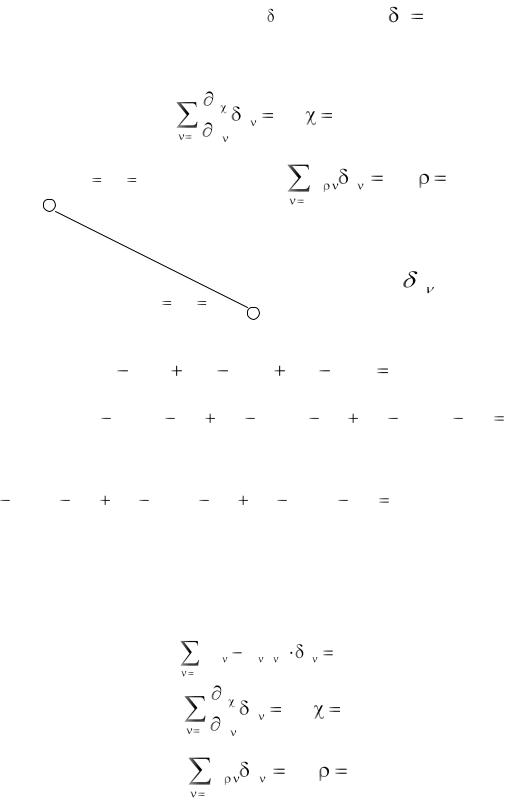
Переходя к определению условий, налагаемых на виртуальные перемещен ия, необходимо учесть, что они мыслятся как перемещения, которые может совершить система при фиксированном моменте времени и должны быть совместимы со связями в этот момент времени. Если голономные связи не зависят от времени, то реальное перемещение может совпасть с одним из возможных, а если голономные связи зависят от времени, то
40
действительное перемещение может не совпасть ни с одним из возможных. Чтобы перейти к записи условий, которые налагают связи на виртуальные перемещения, достаточно в условиях ()
и(0 формально поменять все dx  на x
на x  dt на t 0.
dt на t 0.
В итоге получаем ограничения, накладываемые голономными и неголономными связями на возможные перемещения системы
3N |
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0, |
1,...,k |
|
|
1 |
x |
|
|
|||
|
|
|
|
|
||
|
|
|
3N |
|
|
|
m1 m2 m3 |
|
|
a |
x |
0; |
1,2,...,r |
(x1 , x2 , x3 ) |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ограничения |
|
|
|
k+r |
|
|
ограничений |
наложено на 3N виртуальных |
||
|
|
|
перемещений |
x . |
Следовательно, 3N-k-r |
|
m4 m5 |
m6 |
|
независимых виртуальных перемещений.. |
|||
(x4 , x5 , x6 ) |
|
Пример. 1: Связь - недеформируемый жесткий, |
||||
|
|
|
тонкий стержень. |
|
||
Уравнение связи (x |
x1 )2 |
(x2 |
x5 )2 (x3 |
x6 )2 |
l 2 ; - голономная связь, так как не |
|
входит скорость. Продифференцируем это уравнение |
|
|
||||
( x1 |
x4 )( x1 |
x4 ) |
( x2 x5 )( x1 |
x5 ) ( x3 |
x6 )( x3 |
x6 ) 0 |
Получили голономную связь, хотя в нее входят скорости, так как. эта связь интегрируемая.
Пример 2.
(x1 |
x4 )(x1 |
x4 ) (x2 |
x5 )(x1 |
x5 ) (x3 |
x6 )(x3 |
x6 ) 0 |
- |
|
|
|
|
|
|
|
|
неголономная связь.
Уравнения Лагранжа 1-го рода
Принцип Даламбера-Лагранжа позволяет составить уравнения движения системы (уравнения Лагранжа 1-го рода) с учетом действия на нее идеальных голономных и линейных неголономных связей. Имеем
3N(X m x ) x 0
1
3N |
f |
|
|
|
||
|
|
|
|
|||
|
|
|
x |
0, |
1,...,k |
|
1 x |
||||||
|
|
|
||||
3N |
|
|
|
|
||
|
|
a x |
0; |
1,2,...,r |
||
1 |
|
|
|
|
||
Исходя из записанных равенств, нам необходимо составить уравнения движения системы в виде дифференциальных уравнений. Если бы связей не было, то из первого уравнения, можно было бы получить уравнения движения на основе того, что в таком случае все вариации
