
эл.математика
.pdfМинистерство общего и профессионального образования Российской Федерации
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Е. Я. Файн
МЕТОДИЧЕСКОЕ ПОСОБИЕ
по курсу
“ЭЛЕМЕНТАРНАЯ МАТЕМАТИКА”
для студентов первого курса
физического факультета
г. Ростов — на — Дону
2001 г.

Программа курса “Элементарная математика”.
1.Построение систем координат.
2.Векторы (орты, “плавающие”, “фиксированные” векторы, проекция вектора на ось, компоненты вектора, сложение, вычитание, скалярное и векторное произведения (примеры из школьного курса физики), угол между векторами).
3.Элементарные алгебраические преобразования.
4.Решение простых алгебраических уравнений.
5.Тригонометрические функции, их определение. Формулы приведения, формулы преобразования. Обязательно составление соответствующих таблиц.
6.Графики тригонометрических функций.
7.Графики алгебраических функций.
Обязательно составление серии рисунков:
Рис.1 графики y = 1x , y = x12 , y = x13 ;
Рис.2 графики у = х, у=х2, y=x3
Рис.3 графики у = е-x ,у = еx;
Рис.4 графики у = -е-x ,у = -еx;
Рис.5 графики у =ln(х), у = ln(х);
8.Производная функции, её геометрический смысл.
9.Правила дифференцирования.
1О.Производная сложной функции.
11 .Составление таблицы производных от элементарных функций (обязательно).
12.Построение графиков произведений функций (типа x/(x2-1); x2/(x2+1); (x- 1)e-x; ex/(x+1); e-xsin(x)…).
1З.Построение графиков функций ускорения, скорости, координаты, перемещения,
пути от времени для равномерного и равноускоренного движений. 14.Определённый интеграл. Примеры из школьного курса физики. 15.ГТервообразные элементарных функций.
16.Комплексные числа. Алгебраическая, тригонометрическая, показательная форма комплексного числа. Операции с комплексными числами.
3. Элементарные алгебраические преобразования.
Тождественные преобразования целых рациональных выражений.
При тождественных преобразованиях многочленов часто используют формулы, носящие названия “формул сокращённого умножения”:
a2-b2=(a-b)(a-b) (1) a3-b3=(a-b)(а2+ab+b2) (2) a3+b3=(a+b)(а2-ab+b2) (З) (a+b)2=а2+ab+b2 (4) (a-b)2=а2-ab+b2 (5)
(a+b)3=а3+3a2b+3ab2+b3 (6) (a-b)3=а3-3a2b+3ab2-b3 (7)
При разложении многочлена на множители используют метод вынесения общего множителя за скобки и метод группировки членов.
Пример 1 Разложить на множители многочлен
2х2y+ у 2- 2x3 - ух
Группируя первое и третье, и второе и четвёртое слагаемые и вынося общий множитель в каждой группе, получаем
2х2y+ у 2 – 2x3 – ух = (2x2y – 2x3)+(y2 – yx) = 2x2(y – x) + y(y – x)
Вынося общий множитель (у — х) за скобки, окончательно получаем: 2х2+y2 – 2x3 – ух = (у – х)(2х2 +у)
Пример 2 Разложить на множители многочлен
x3+x2+x-3
Покажем, как, последовательно используя метод группировки, формулы (1) и
(2) и метод вынесения общего множителя, можно разложить на множители этот многочлен.
x3+x2 +х—З = (х3 – 1)+(х2 – 1)+(х—1) = =(х – 1)(х2 +х+1)+(х – 1)(х+1)+(х – 1)= =(х – 1)(х2+х+1+х+1+1)=(х – 1)(х2 +2х+3)
Пример 3

Разложить на множители многочлен
3x2y4 – 24x5y = 3x2y(y3 – 8x3) = 3x2y(y – 2x)(y2 + 2xy + 4x2)
Тождественные преобразования дробных рациональных выражений.
Пример 1 Упростить выражение
|
x |
|
x2 |
+1 |
|
x2 − x +1 |
2x2 + x +1 |
|
||||
|
|
|
+ |
|
|
|
|
|
: |
|
|
. |
|
|
x3 |
+1 |
x −3 |
x +1 |
|||||||
x −3 |
|
|
|
|
||||||||
Преобразуем данное дробное рациональное выражение в несократимую дробь, у которой числитель и знаменатель — многочлены.
При преобразовании выражений сначала производят действия умножения и деления, а затем сложения и вычитания. Если в выражении имеются скобки, то сначала производят действия в скобках.
Произведём умножение дробей во втором слагаемом в скобках:
x2 |
+1 |
|
x2 − x +1 |
= |
(x2 +1)(x2 − x +1) |
= |
x2 |
. |
|
x3 |
+1 |
|
x −3 |
(x3 +1)(x −3) |
(x +1)(x −3) |
||||
|
|
|
|
|
|||||
Здесь при сокращении использована формула х3 + 1 = (х + 1)(х2 – х + 1). складываем дроби в скобках:
|
x |
|
+ |
x2 +1 |
|
= |
|
x(x +1) |
|
+ |
x2 +1 |
= |
2x2 + x +1 |
. |
|||
|
x −3 |
(x +1)(x −3) |
(x |
+1)(x − |
3) |
(x +1)(x −3) |
|
||||||||||
|
|
|
|
|
(x +1)(x −3) |
||||||||||||
и производим деление |
|
|
|
|
|
|
|
|
|
||||||||
|
2x2 + x +1 |
: 2x2 + x +1 |
= |
1 |
. |
|
|
|
|
|
|
||||||
|
|
x −3 |
|
|
|
|
|
|
|||||||||
|
(x +1)(x −3) |
x +1 |
|
|
|
|
|
|
|
|
|
||||||
Тождественные преобразования иррациональных выражений.
Для любого рационального числа r = m/n, где m— целое, n — натуральное и,
для любого действительного числа а>0 число n am называется степенью числа a c показателем r и обозначается аr. Следовательно, если r=m/n, то
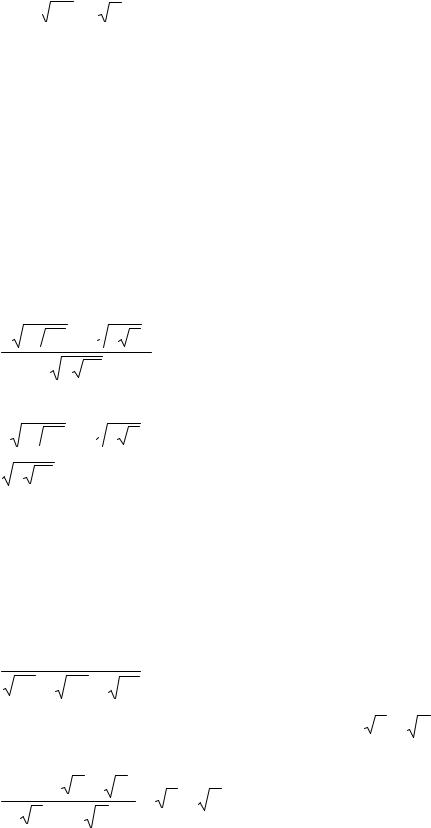
a r = n a m = (n a )m
Из этого определения и свойств степеней с целыми показателями основные свойства степеней с действительными показателями:
ar·as=ar+s (8) ar:as=ar-s (9) (ar)s=ars (10)
(ab)r = ar·br (11) (a/b)r = ar/br (12)
Пример 1 Найти значение выражения:
53 2 27 + 2
27 + 2  33 4 x 4 93 16
33 4 x 4 93 16
Преобразуем выражения, стоящие в числителе и знаменателе:
53 2 27 + 2
27 + 2  33 4 = 5 21 / 3 31 / 2 + 2 31 / 2 21 / 3 = 7 21 / 3 31 / 2
33 4 = 5 21 / 3 31 / 2 + 2 31 / 2 21 / 3 = 7 21 / 3 31 / 2
4 93 16 = 32 / 3 21 / 3
В результате получаем
|
7 21 / 3 31 / 2 |
= 7 |
|
31 / 2 21 / 3 |
|
|
|
Пример 2 Освободиться от иррациональностей в знаменателе дроби
x − y
3 x 2 + 3 y 2 + 3 xy
Умножим числитель и знаменатель дроби на 3 x − 3 y и воспользуемся формулой (2) получим
(x − y)(3 x |
− 3 y) |
= 3 |
x − 3 |
y. |
|
(3 x)3 − (3 y )3 |
|||||
|
|
|
|||
Задания для самостоятельной работы
Упростить выражения:
1. |
|
4 |
+ |
1 |
− |
4 |
; |
|
x3 |
+ 2x 2 |
x 2 + 4x + 4 |
x 4 + 4x3 + 4x 2 |
|||||
|
|
|
|

2. |
|
|
|
|
x 4 −16 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
x 4 − 4x3 + 8x 2 −16x +16 |
|
|
|
|
|
|
|
|
|
|||||||
3. |
|
x |
+ |
x 2 |
|
x 2 − 2x + |
4 |
: |
|
8 |
− |
x 2 |
+ x + 6 |
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x3 + 8 |
2 − x |
|
x 2 |
− 4x + 4 |
4x + 8 |
|||||||||||
|
x − 2 |
|
|
|
|
|
|
|
|||||||||
Разложить на множители:
4.(аb + ас + bс)(а + b + с) – abc;
5.bс(b + с) + ас(с – а) – ab(a+b);
6.(а + b + с)3 – a3 – b3 – c3;
7.a3+5a2+3a-9;
8.а2b2(b – a) + b2c2(c – b) + a2c2(a – c);
9.а5 + а4 + а3 + а2 + а + 1;
10.а3+b3+c3-3abc;
11.у3(a – x) – x3(a – y) + a3(x – y);
12.2а2b + 4ab2 – a2c + ac2 – 4b2c + 2bc2 – 4abc;
13.у(х – 2z)2 + 8хyz + x(y – 2z)2 – 2z(х+у)2;
14.х3 + 9х2 + 11х – 21;
15.x3(x2 – 7)2 – 36x;
16.(b – c)3 + (c – a)3 + (a – b)3;
17.а4 + 8a3 – 3a2 – 24a – 2a – 16;
18.х4 + у4 +z4 – 2х2y2 – 2х2z2 – 2у2z2;
19.(х – y)3 + (y – z)3 +(z – x)3;
20.(х2 + х + 1)2 + 5(х2 + 6х + 1)(х2 + 1) + 2(х2 + 1)2;
21.2(х2 + 6х + i)2 + 5(х2 + 6х + 1)(х2 + 1) + 2(x2 + 1)2;
22.Разложить выражения ba − ba - на два множителя, из которых один равен
ba + ba
Выполнить алгебраические преобразования:
23. |
(x 2 − y 2 − z 2 + 2 yz) : |
x + y − z |
; |
|
x + y + z |
||||
|
|
|
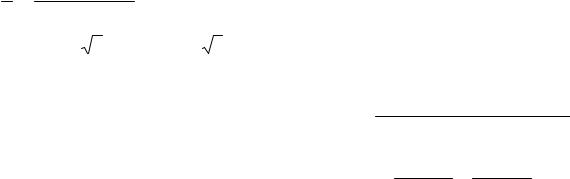
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
a |
2 |
−1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
a |
− an |
3 |
|
− n |
4 |
+ n |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
24. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
n2 + an |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 − a 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x + x 2 |
|
|
|
|
|
|
||||||||||
25. |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
||||||||||||||||
|
|
ax |
|
− 2a 2 |
|
|
x 2 + x − 2ax − 2a |
|
|
|
3 + x |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x − 6 |
|
|
|
|
|
|||||||||||
26. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + |
|
|
|
|
|
|
|
; |
|
|
|
|
|||||||||||
|
|
a 2 |
|
− 4x 2 |
|
|
|
2x 2 + 6x − ax − 3a |
|
|
|
x |
− 2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
27. |
|
2a +10 |
|
|
|
|
|
130 − a |
|
|
|
|
30 |
|
|
|
|
|
|
|
3a |
3 |
+ 8a 2 |
− 3a |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
− |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − 3a |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
1 + 0,25a 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
3a −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
28. |
|
|
a 2 |
|
− b2 |
|
− |
a3 |
− b3 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
a − b |
a 2 |
− b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
29. |
|
|
|
|
|
x |
|
|
|
− |
y(x − y)2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
x 2 |
|
+ y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 |
|
− y 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30. 2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
3 |
|
|
|
|
2x |
+ |
1 |
|
|
|
|
|
|
|
|
|
2x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
+ |
|
|
|
|
1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
31. |
|
|
a −1 |
|
|
|
|
|
|
|
|
|
|
|
2(a −1) |
|
|
|
|
|
|
|
4(a +1) |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
+ |
|
|
|
− |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
− 2a + |
2 |
|
|
|
a 2 − 4 |
|
|
|
a 2 + a − 2 |
|
a 2 − 3a |
+ |
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3(x + |
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x 2 − x −10 |
|
|
|
|
|
|
|
|
5 |
|
|
|||||||||||||||||||||||||||||||||||
32. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
||||
|
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
+ x |
|
|
+ x +1) 2(x |
− x |
+ x −1) |
|
|
|
|
+1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2(x |
|
|
|
|
|
|
|
|
|
|
x |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
36a3 −144a − 36a 2 +144 ; a3 + 27
+ 2(x3+1) − 2(x3−1) ;
|
|
x − y |
|
|
|
x 2 + y 2 |
+ y − 2 |
|
|
4x 4 + |
4x 2 y + y 2 − 4 |
|
|||||||||||||||||||||
33. |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
2 y |
− x |
|
|
|
|
x |
|
− xy |
− 2 y |
|
|
|
x |
+ y + xy + x |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
a 2 + a − 2 |
|
|
(a + 2)2 − a 2 |
|
|
3 |
|
|
|
|||||||||||||||||||||||
34. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
; |
|
||||
a n+1 − 3a n |
|
|
|
4a 2 |
− 4 |
|
|
a 2 −1 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2a |
2 |
(b + c) |
2n |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
− |
|
|
|
|
: |
2a(b + c)n −1 |
|
|
|
|
|
|||||||||||||||||
35. |
|
|
|
|
2 |
|
|
= A : B; |
|
||||||||||||||||||||||||
an2 − a3 − 2a 2 − a |
a 2 c − a(nc − c) |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
36. |
|
|
|
1 |
|
|
|
|
|
|
|
|
+ |
|
|
|
1 |
|
|
|
|
+ |
|
|
|
|
1 |
|
; |
||||
a(a − b)(a − c) |
b(b − a)(b − c) |
c(c − a)(c − b) |
|
||||||||||||||||||||||||||||||

|
1 + (a + x)−1 |
|
|
1 |
− (a 2 + x 2 ) |
||||
37. |
|
|
|
1 |
− |
|
|
|
; |
1 |
− (a + x)−1 |
|
|
2ax |
|||||
|
|
|
|
|
|
||||
после упрощения результат вычислить при x = a 1−1 .

4. Решение простых алгебраических уравнений.
Линейные уравнения.
Линейным уравнением с одной переменной х называют уравнение вида ах=b, где а и b — действительные числа.
для линейного уравнения ах=b могут представиться три случая:
1.а≠0; в этом случае корень уравнения равен a/b;
2.а=0, b=0; в этом случае уравнение принимает вид 0*х=0, что верно при любом х, т.е. корнем уравнения служит любое действительное число;
З. а=0, b≠0; в этом случае уравнение принимает вид 0*х=b, оно не имеет корней.
Пример1
Решить уравнение |
1 |
x + |
|
2 |
= 0 |
|
5 |
15 |
|||||
|
|
|
||||
Решение
Перенесём известное слагаемое в правую часть, изменив его знак 15 x = −152 .
Разделим обе части этого уравнения на коэффициент при х: x = −152 + 15 , т.е.
x = − 23 .
Квадратные уравнения.
Теорема Виета.
Если квадратное уравнение ах +bх+с=0 имеет действительные корни х1 и х2,
то их сумма равна − ba и произведение равно ac :
Для приведенного квадратного уравнения х2 + рх + q = 0:
х1 + х2 = -р, х1х2=q.
Пример1
Решить уравнение:
х2-9x+14=0
Решение:
Найдем два числа х1 и х2, такие, что

х1 + х2 = 9, х1 х2=14.
Такими числами являются 2 и 7. Они и являются корнями заданного уравнения.
Формула
x |
= −b ± b2 − 4ac |
1,2 |
2a |
|
показывает, что при решении квадратного уравнения ах +bх+с=0 могут представиться три случая:
1.b2-4ac>0; в этом случае два корня уравнения действительны и различимы между собой.
2.b2-4ac=0 тогда два корня уравнения действительны и равны между собой: x1 =x 2 = − 2ba .
3.b2-4ac<0 тогда оба корня уравнения мнимы.
Если квадратное уравнение имеет вид ах2 +2kс+с=0, то удобнее находить корни по формуле
x |
= − k ± k 2 − ac |
1,2 |
a |
|
Корни приведённого уравнения находятся по формуле
x |
= − p ± |
|
|
p2 |
− q |
|
|
|
|
|
|
|
|
|
||||||||||||
1,2 |
2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решить уравнения: |
|
|
6 − x |
|
||||||||||||||||||||||
38) |
1 |
|
−1 = |
|
|
|
1 |
|
|
|
|
− |
|
|
||||||||||||
2 − x |
|
x |
− |
2 |
3x2 −12 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
39) |
3 |
|
− |
|
4 |
|
|
= |
|
|
|
|
1 |
|
|
− |
|
2 |
|
|
|
|||||
x − 2 |
|
x −1 |
|
|
x − |
4 |
|
x −3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
40) |
30 |
|
|
− |
|
|
13 |
|
|
|
|
|
|
= |
|
7 +18x |
||||||||||
x2 −1 |
|
x2 + x +1 |
|
x3 −1 |
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
41) |
2x |
|
+ |
|
|
x |
= |
|
|
|
|
|
b2 |
|
|
|
|
|
|
|||||||
x +b |
|
x −b |
|
|
4x2 − 4b2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
42) |
1 |
|
|
|
|
|
− |
|
|
|
1 |
|
|
|
|
= |
|
|
|
|
a(x −1) |
|||||
ax − cx2 |
|
|
a |
−c |
a2 − acx − ac + c2 x |
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
43) |
7a + 6b |
|
− |
3ay |
=1 − |
|
|
ay |
|
|||||||||||||||||
6b |
|
|
|
|
2b2 |
b2 |
|
− ab |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
44) ax −b + bx + a |
|
= a2 |
+ b2 |
|||||||||||||||||||||||
|
a +b |
|
|
|
|
a −b a2 −b2 |
||||||||||||||||||||
