
эл.математика
.pdf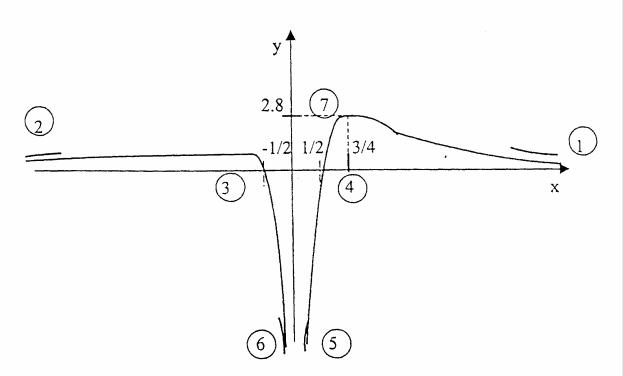
|
3 |
|
|
|
|
|
|
|
x = |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||
|
|
|
64 |
|
224 |
|
||
|
32 |
|
|
|
||||
y = |
|
|
− |
|
= |
|
≈ 2.8 |
|
9 |
81 |
81 |
||||||
|
|
|
|
|||||
Далее можно взять вторую производную, а можно и не брать, т.к. других экстремумов нет, то гладкое соединение точек даёт рисунок:
Приложение 2.

Построить графики функций
1) |
y = |
1 + x 2 |
|
|
; |
|
|
|
|
|
|
|
|
||||||||
1 − x 2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4) |
y = − |
1 |
+ |
|
|
2 |
|
|
− |
|
1 |
||||||||||
|
|
|
|
x 2 |
|
x3 |
|||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
||||||||||
7) |
y = |
|
1 |
+ |
|
1 |
|
|
; |
|
|
|
|||||||||
x3 |
|
x5 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
10) |
y = |
|
|
|
|
e−x |
|
|
|
|
|
; |
|
|
|
|
|||||
1 |
− x 2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
13) |
y = |
|
|
|
|
e x |
|
|
|
|
|
; |
|
|
|
|
|||||
1 |
− x 2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
16) |
y = |
e−x + e x |
; |
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
19) |
y = e−x sin(x); |
|
|||||||||||||||||||
22) |
y = e x cos(x); |
|
|||||||||||||||||||
25) |
y = 5 sin 2 (x); |
|
|||||||||||||||||||
28) |
y = x + sin(x); |
|
|||||||||||||||||||
31) |
y = |
|
|
|
|
x 2 |
|
|
|
|
; |
|
|
|
|
||||||
|
|
sin(x) |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
34) |
y = x 2 − sin 2 (x); |
||||||||||||||||||||
37) |
y = x 4 (12 ln(x) − |
||||||||||||||||||||
;
7);
2)y =1 + x3 ;
1− x3
5)y = 2xx−2 1 ;
8) |
y = |
|
e−x |
|
|
|
; |
||
|
x 2 |
+1 |
|||||||
|
|
|
|
||||||
11) |
y = |
|
e x |
|
|
; |
|||
x 2 |
+ |
1 |
|||||||
|
|
|
|
||||||
14) |
y = x 2 e−x ; |
|
|||||||
17) |
y = (x 4 |
−1)e x ; |
|||||||
20) |
y = e x |
sin(x); |
|||||||
23) |
y = e−x |
cos(x); |
|||||||
26) |
y = x sin(x); |
||||||||
29) |
y = x 2 + sin(x); |
||||||||
32) y = cos(x) + sin(x);
35) y = (x −1)2 ; sin(x)
38) y = ln(x) + sin(x);
3) y = |
|
|
1 |
|
|
|
+ |
|
1 |
; |
|||
|
x3 |
|
|
|
|
x5 |
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
6) |
y = |
1 + |
|
x3 |
|
; |
|
||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 − x3 |
|
|
||||||||||
9) |
y = |
|
|
|
e−x |
|
; |
|
|||||
|
x 2 −1 |
|
|||||||||||
|
|
|
|
|
|
||||||||
12) |
y = |
|
|
|
e x |
|
; |
|
|||||
|
x 2 −1 |
|
|||||||||||
|
|
|
|
|
|
||||||||
15)y = −x 2 e x ;
18)y = (x3 −1)e−x ;
21)y = e−x sin 2 (x);
24)y = e x cos3 (x);
27)y = sin(x x) ;
30)y = sin(x 2x) ;
33)y = cos(x x) + sin(x x) ;
36)y = (x +1)3 ; sin(x)
39)y = ln(x) + cos(x);

Комплексные числа
На множестве действительных чисел не всякое уравнение четной степени имеет решение. Так, например, уравнение х2+1=0 не имеет действительных корней, поскольку не существует действительного числа, квадрат которого равен числу -1. Это привело к расширению множества действительных чисел путем введения чисел новой природы. Эти новые числа называют мнимыми.
Число, удовлетворяющее равенству х2 = -1, обозначают буквой i, оно называется мнимой единицей.
Таким образом,
i2 = - 1
Комплексным числом называется упорядоченная пара чисел, где a и b — действительные числа.
Упорядоченная пара (а;b)≠(b;а)
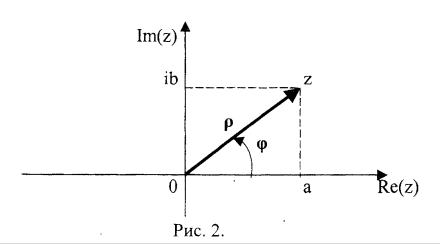
Комплексное число определяет точку на плоскости и в алгебраической форме записывается
z=а+ib.
Числа а и ib называются соответственно действительной и мнимой частями комплексного числа
а=Re(z), ib=Im(z).
Комплексное число можно изобразить стрелкой. Комплексно - сопряженным называется число z * = а-ib.
Операции над комплексными числами.
1)Операция сложения z1+z2 =(а1 +а2, b1 +b2).
2)Операция вычитания z1 - z2 =(а1 - а2, b1 - b2). З) Вводится комплексный ноль z + (-z) = 0.
4)Операция умножения
5) z·z*= (a2 + b2, ab - ba) = (a2+b2, 0) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
z |
|
= |
z z |
(a + ib )(a |
2 |
−ib ) |
= |
a a + b b + i(a b − a b ) |
a a + b b |
|
, |
i(a b − a b ) |
||||||||||
|
|
1 |
1 |
= |
1 |
2 |
2 |
1 2 1 2 |
2 |
2 |
= |
2 |
2 |
2 |
2 |
2 |
|
||||||
|
|
|
2 |
|
1 |
2 |
|
|
2 1 1 2 |
|
1 2 |
1 |
|
2 1 |
1 2 |
|
|||||||
|
z2 |
|
z2 |
z2 |
|
a2 + b2 |
|
|
|
a2 + b2 |
a2 + b2 |
|
|
a2 + b2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Как видно, операция сложения и вычитания в алгебраической форме производить удобно, а деления и умножения – нет.
Тригонометрическая форма комплексного числа.
φ = arg(z) – аргумент комплексного числа (это угол отклонения в положительном направлении от действительной оси).
Пределы, в которых находится аргумент φ , определим следующим образом
–π < φ ≤ π
Так как аргумент комплексного числа функция периодическая, то определим
Arg(z) = arg(z) + 2πn, nЄz
ρ - модуль комплексного числа, расстояние от начала координат. По теореме Пифагора
 поэтому, подставляя полученное в алгебраическую форму комплексного числа:
поэтому, подставляя полученное в алгебраическую форму комплексного числа:
z = ρ(cos(φ) + i·sin(φ)).
Показательная (экспоненциальная) форма комплексного числа.
Так как экспонента представима в виде ряда: |
|
|
|
|
|
|
e x =1 + x + |
x 2 |
+ |
x3 |
+ |
x 4 |
+..., |
|
|
|
||||
2 |
6 |
24 |
|
|||
то, следовательно,
e iix = 1 + ix − |
x 2 |
− i |
x 3 |
+ |
x 4 |
+ i |
x 5 |
..., |
|
2 |
6 |
24 |
12 |
||||||
|
|
|
|
|

a e−iix =1 − ix − |
x 2 |
+ i |
x3 |
+ |
x 4 |
+ i |
|
x5 |
|
|
..., |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
6 |
|
24 |
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
И тогда, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
2 |
|
|
x |
4 |
|
|
|
|
|
∞ |
|
|
n |
x |
2n |
|
e |
ix |
+ e |
−ix |
|
|
|
||||||||
cos(x) =1 − |
|
|
|
+ |
|
+... = ∑(−1) |
|
|
|
|
= |
|
|
|
, и |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
(2n)! |
|
|
2 |
|
|
|
|
|
|||||||||||||||||||
2! |
|
|
|
4! |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
x |
3 |
|
|
x |
5 |
|
|
x |
7 |
|
|
∞ |
|
|
|
|
|
|
x |
2n+1 |
|
e |
ix |
− e |
−ix |
|||||||
sin(x) = x − |
|
|
+ |
|
− |
|
+... = ∑(−1)n |
|
|
|
|
= |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
(2n +1)! |
|
|
2 |
|
|||||||||||||||||||||||
3! |
|
|
|
5! |
7! |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Таким образом,
ϑ = eiϑ − e−iϑ sin( )
2i
ϑ = eiϑ + e−iϑ cos( )
2
Подставив в z = ρ·i(cos(φ) + i·sin(φ))=½ρ(eiφ + e-iφ + eiφ – e-iφ) , получим показательную
(экспоненциальную) форму комплексного числа: z = ρeiφ
Теперь, представляя комплексное число в такой форме, удобно производить операции умножения, деления и возведения в степень.
z = z1z2 = ρ1ρ2ei(φ1 + φ2)
то есть, умножение сводится к изменению модуля в ρ2 раз:
ρ = ρ1ρ2
и повороте на угол φ2:
φ = φ1 + φ2
Аналогично, деление:
Возведение в целую степень:
zn = ρneinφ
Извлечение корня:
z1/n = ρ1/n·ei(φ+2πκ)*1/n
Здесь n ρ арифметический корень, а к =0, 1, 2, . .. ,n-1. Корень степени n на множестве
комплексных чисел имеет n различных значений. Исключение составляет z = 0. В этом случае все значения корня равны между собой и равны нулю.
Модуль корня n-й степени из комплексного числа равен корню той же степени из модуля подкоренного числа, а аргумент для каждого значения корня определяется по формуле

ϕk = ϕ + 2πk , где k=0,1,2,…,n-1 n
Пример 1 z =1 + i 3
3
Решение Наидем модуль числа
ρ =  a 2 + b2 , тогда
a 2 + b2 , тогда
cos(ϕ) = ρa = 12
sin(ϕ) = ρb = 23
следовательно,ϕ = π3 .
И, таким образом
z= 2eiπ/3
Возведем это число в 5-ую степень
z5= 25ei5π/3
При возведении в степень необходимо, чтобы аргумент оставался в пределах –π < φ ≤ π.
z5= 25ei(5π/3-2π)= 25e-iπ/3
Операция извлечения корня из комплексного числа неоднозначна.

π
z =1 + i 3 = 2 ei 3
3 = 2 ei 3
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
k |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
+2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
uk |
= zk3 = 3 |
|
2e |
|
9 |
|
3 |
, k = 0,1,2. |
|
||||||||||||||||
u0 |
= 3 2ei |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
π |
|
|
6π |
|
|
|
|
|
|
|
|
7π |
|
||||||||
|
|
|
|
i |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
u1 = 3 2e |
9 9 |
|
|
= 3 |
2ei 9 |
|
|||||||||||||||||||
|
|
|
|
π |
|
|
12π |
|
|
|
|
|
|
13π |
5π |
||||||||||
|
|
|
|
i |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
u2 = 3 2e 9 |
|
|
9 |
|
|
= 3 |
2ei 9 = 3 2e−i 9 |
||||||||||||||||||
Пример2.
Дано число z=-i Найти z-1/3
Решение
ρ = 0 +1 =1
cos(ϕ) = 0sin(ϕ) = −1
Т.е. ϕ = π2 Итак, z=e-i π/2
Uk = ei(-π/2+2πκ)(-1/3)= ei(π/6+2πκ/3)
Находим:
U0=ei π/6 U1= ei (π/6 - 2π/3)
U2 = ei(π/6+4π/3)= e-i(7π/6)= ei(5π/6)
Звезда корней (-i)-1/3:

Пример 3
Дано число z=1 Найти z1/4
Решение
ρ =  1 + 0 =1
1 + 0 =1
cos(ϕ) =1sin(ϕ) = 0
Т.е. φ=0. Итак, z=e-i*0.
U k = zk 14 = ei(0+2πk )( 14 ) = ei(π 2 ) k
Находим:
U0 |
= ei * 0 =1; |
U1 = ei(π / 2) = i; |
|
U 2 |
= eiπ = −1; |
U3 |
= ei(3π / 2) = −i; |
Звезда корней (1)1/4:

Задания для самостоятельного решения
1) |
Найти z=z1-z2 |
|
|
|
z1 |
=1 − i |
3, |
|
z2 |
= −2 + 2i |
|
2) |
Найти z=z1+z |
|
|
|
z1 |
=1 + i |
3, |
|
z2 |
=1 − i |
|
3) |
Найти z=z1-z2 |
|
|
|
z1 |
=1 − i, |
|
|
z2 |
=1 − i |
3 |
4) |
Найти z=z1-z2 |
|
|
|
z1 |
=1 + i |
3, |
|
z2 |
=1 − i |
|
5) |
Найти z=z1+z2 |
|
|

|
|
|
|
|
z1 |
= |
3 − i, |
|
|
|
|
|
|
z2 |
=1 − i |
|
|
6) |
Найти z=z1+z2 |
|
|
|
||||
|
|
|
|
|
z1 |
= i + |
3, |
|
|
|
|
|
|
z2 |
=1 − i |
|
|
7) |
Найти z=z1-z2 |
|
|
|
||||
|
|
|
|
|
z1 |
= i + |
3, |
|
|
|
|
|
|
z2 |
=1 − i |
|
|
8) |
Найти z=z1-z2 |
|
|
|
||||
|
|
|
|
|
z1 |
= i + |
3, |
|
|
|
|
|
|
z2 |
=1 − i |
3 |
|
9) |
Найти z=z1+z2 |
|
|
|
||||
|
|
|
|
|
z1 |
= i − |
3, |
|
|
|
|
|
|
z2 |
=1 − i |
3 |
|
10) |
Найти z=z1+z2 |
|
|
|
||||
|
|
|
|
|
z1 |
=1 − i, |
|
|
|
|
|
|
|
z2 |
=1 − i |
3 |
|
11) |
Найти z6 |
|
2 |
|
||||
|
|
|
|
|
z = |
2 |
||
|
Найти z5 |
i |
− |
|||||
12) |
|
2i |
|
|||||
|
|
|
|
|
z = |
3 |
||
|
1 |
|
|
|
i |
− |
||
|
|
|
|
|
|
|
||
|
Найти z |
|
и нарисовать звезду корней |
|
||||
13) |
3 |
|
||||||
|
|
|
|
|
z =1 + i |
3 |
||
|
Найти z7 |
|
2 |
|
||||
14) |
|
|
|
|||||
|
|
|
|
|
z = i + |
3 |
||
|
Найти z11 |
|
2 |
|
||||
15) |
|
2 |
|
|||||
|
|
|
|
|
z = |
3 |
||
|
1 |
|
i |
− |
||||
|
|
|
|
|
||||
|
Найти z8 , z |
|
|
|
|
|
||
16) |
5 |
|
|
|
||||
|
|
|
|
|
z = i − |
3 |
||
|
Найти z4 |
|
2 |
|
||||
17) |
|
|
|
|||||
