ponomorenko

НАУЧНО-ИНФОРМАЦИОННЫЙ ЦЕНТР САНКТ-ПЕТЕРБУРГСКОГО ГОСУДАРСТВЕННОГО ТЕХНОЛОГИЧЕСКОГО УНИВЕРСИТЕТА РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ

Рис.1.18. Схема электрической цепи для расчета токов в ветвях методом контурных токов

Составим систему уравнений для первого и второго контуров:

I11 (R1 + R4 + R3 ) − I 22 R4 + JR3 = E1 ,

I 22 (R4 + R2 + R5 ) − I11 R4 + JR5 = −E2 .

Решая эти уравнения, найдем контурные токи I11, I22. Искомые токи в ветвях:

I1 = I11, I2 = I22 , I3 = I11 + J , I4 = I11 − I22 , I5 = I22 + J .

Для проверки правильности расчета токов можно составить баланс мощностей.

1.9. Метод узловых потенциалов

Метод основан на первом законе Кирхгофа, т.е. позволяет уменьшить количество расчетных уравнений до п -1.

При составлении уравнений по методу узловых потенциалов потенциал одного из узлов принимают равным нулю. В этом случае токи в схеме не изменяются, так как никаких новых ветвей, по которым могли бы протекать токи, не образуется. Для определения потенциалов оставшихся (п -1) узлов на основе первого закона Кирхгофа пользуются следующим правилом: потенциал рассматриваемого узла умножается на сумму проводимостей ветвей, присоединенных к этому узлу; от этого слагаемого вычитаются произведения потенциалов соседних узлов на сумму проводимостей ветвей между рассматриваемым узлом и соответствующим соседним узлом; правая часть уравнения равна алгебраической сумме произведений ЭДС в каждой ветви на проводимость ветви, присоединенной к рассматриваемому узлу;

20

НАУЧНО-ИНФОРМАЦИОННЫЙ ЦЕНТР САНКТ-ПЕТЕРБУРГСКОГО ГОСУДАРСТВЕННОГО ТЕХНОЛОГИЧЕСКОГО УНИВЕРСИТЕТА РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ

произведение вида EG записывается с положительным знаком, если ЭДС направлена к узлу, для которого записывается уравнение, и с отрицательным, если ЭДС направлена от узла. Если схема содержит не только источники ЭДС, но и источники тока, то токи источников тока учитываются также в правой части уравнения, причем с положительным знаком записываются токи источников тока, направленные к рассматриваемому узлу, с отрицательным – от узла.

Из полученной системы уравнений определяются потенциалы узлов. Затем произвольно задаются направлениями токов в ветвях и рассчитывают токи по закону Ома. Например, для узлов 1,2 и 3 схемы (рис.1.19) (при φ4 =0) получим соответственно следующие уравнения:

Из формулы (1.18) определяются потенциалы φ1, φ2, φ3.

Рис.1.19. Схема электрической цепи для расчета токов методом узловых потенциалов

При выбранных направлениях токи в ветвях равны:

21

НАУЧНО-ИНФОРМАЦИОННЫЙ ЦЕНТР САНКТ-ПЕТЕРБУРГСКОГО ГОСУДАРСТВЕННОГО ТЕХНОЛОГИЧЕСКОГО УНИВЕРСИТЕТА РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ

Если в схеме имеется идеальный источник ЭДС и сопротивлений в этой ветви нет, то потенциал одного узла ветви принимается за нуль, тогда потенциал другого узла этой ветви будет определяться величиной ЭДС. Число уравнений для исходной схемы уменьшается.

Так, если в схеме (рис.1.19) сопротивление R2=0, то приняв φ4 =0, получим φ2 =Е2. Остается записать уравнения для узлов 1,3. Ток I2 в этом случае определяется по первому закону Кирхгофа.

Частным случаем метода узловых потенциалов является метод двух узлов, который удобно применять для схем, имеющих всего два узла (рис.1.20). Если принять потенциал точки в за нуль (φв=0), тогда потенциал точки а можно определить по общему правилу:

Рис.1.20. Схема с двумя узлами

В общем случае напряжение между двумя узлами может быть определено по следующей формуле:

где – алгебраическая сумма произведений ЭДС на проводимость ветви с соответствующей ЭДС (с положительным знаком записываются ЭДС, направленные к узлу а), ∑J K – алгебраическая сумма токов источников тока (с положительным знаком записывается ток источника, направленный к узлу а), ∑GK – арифметическая сумма проводимостей всех ветвей между двумя узлами.

22

НАУЧНО-ИНФОРМАЦИОННЫЙ ЦЕНТР САНКТ-ПЕТЕРБУРГСКОГО ГОСУДАРСТВЕННОГО ТЕХНОЛОГИЧЕСКОГО УНИВЕРСИТЕТА РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ

1.10. Принцип и метод наложения

Для линейных электрических цепей справедлив принцип наложения, который формулируется следующим образом: ток в любой ветви равен алгебраической сумме токов, вызываемых каждым источником энергии.

Принцип наложения положен в основу метода расчета, получившего название метода наложения.

Если в электрической цепи заданными являются ЭДС источников и токи источников тока, то расчет токов в ветвях состоит в следующем: поочередно рассчитывают токи, возникающие от действия каждого из источников энергии, мысленно удаляя остальные источники из схемы, но оставляя в схеме внутренние сопротивления источников. При этом надо иметь в виду, что когда ведется расчет токов, вызванных каким-либо одним источником ЭДС или тока, то остальные источники ЭДС в схеме заменяются короткозамкнутыми участками, а источники тока – размыкаются.

Ток в каждой ветви определяется как алгебраическая сумма токов от всех источников энергии.

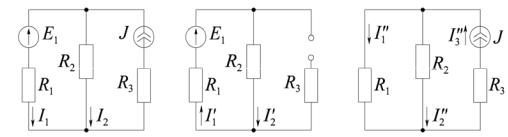
В качестве примера приведен расчет для схемы (рис.1.21,а).

Рис.1.21. Схема электрической цепи (а) для расчета токов в ветвях методом наложения (б,в)

Для схемы (рис.1.21,б) определим токи от источника ЭДС:

Для схемы (рис.1.21,в) определим токи от источника тока:

Результирующие токи в ветвях схемы (рис.1.21,а) вычислим как алгебраическую сумму найденных токов:

23

НАУЧНО-ИНФОРМАЦИОННЫЙ ЦЕНТР САНКТ-ПЕТЕРБУРГСКОГО ГОСУДАРСТВЕННОГО ТЕХНОЛОГИЧЕСКОГО УНИВЕРСИТЕТА РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ

1.11. Метод эквивалентного генератора напряжения (активного двухполюсника)

Метод позволяет определить ток в какой-либо одной ветви сложной электрической схемы. Всю остальную схему относительно рассматриваемой ветви можно представить в виде активного двухполюсника (рис.1.22,а). Двухполюсник – это обобщенное название схемы, которая двумя выходными зажимами (полюсами) присоединена к выделенной ветви. Двухполюсник называется активным, если в нем есть источник энергии. В этом случае в прямоугольнике, изображающим двухполюсник, ставят букву А. Если в двухполюснике нет источников энергии, то его называют пассивным. В этом случае в прямоугольнике не ставят никакой буквы.

Рис.1.22. Схемы для определения тока в ветви (а) методом эквивалентного генератора (б,в)

По отношению к выделенной ветви ав, сопротивление которой R, активный двухполюсник можно заменить эквивалентным генератором, ЭДС Е которого равна напряжению холостого хода на зажимах разомкнутой ветви (рис.1.22,б), а внутреннее сопротивление равно входному сопротивлению RBX пассивного двухполюсника ( рис.1.22,в) со стороны точек ав.

Расчет схемы в режиме холостого хода для определения напряжения Uaвх=Е проводится любым расчетным методом.

Для определения RBX активный двухполюсник заменяется пассивным путем исключения источников энергии (источники ЭДС заменены короткозамкнутыми участками, а ветви с источниками тока размыкаются).

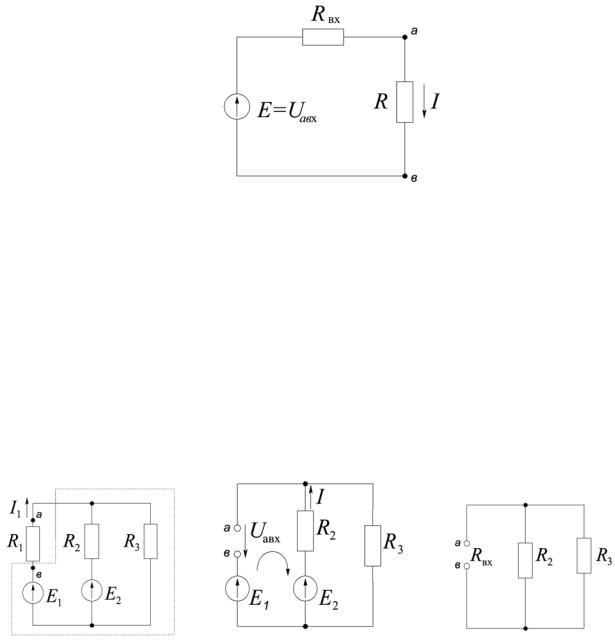
Таким образом, исходная схема (рис.1.22,а) заменяется схемой рис.1.23, в которой искомый ток равен

НАУЧНО-ИНФОРМАЦИОННЫЙ ЦЕНТР САНКТ-ПЕТЕРБУРГСКОГО ГОСУДАРСТВЕННОГО ТЕХНОЛОГИЧЕСКОГО УНИВЕРСИТЕТА РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ

Рис.1.23. Схема для замены активного двухполюсника эквивалентным генератором

Рекомендуется следующая последовательность расчета:

1)найти напряжение Uавх на зажимах разомкнутой ветви ав,

2)определить входное сопротивление RВХ всей схемы по отношению к зажимам ав для пассивного двухполюсника,

3)подсчитать ток по формуле 1.20.

Ниже приведен пример расчета тока I1 методом эквивалентного генератора (рис.1.24,а).

Рис.1.24. Схемы для расчета тока методом эквивалентного генератора (а), напряжения Uавх (б) и RВХ (в)

Для определения напряжения Uавх воспользуемся схемой рис.1.24,б. Направление напряжения Uавх выбрано произвольно.

Определим ток через сопротивление R2:

Напряжение Uавх определим из второго закона Кирхгофа для контура, в который входит это напряжение:

25

НАУЧНО-ИНФОРМАЦИОННЫЙ ЦЕНТР САНКТ-ПЕТЕРБУРГСКОГО ГОСУДАРСТВЕННОГО ТЕХНОЛОГИЧЕСКОГО УНИВЕРСИТЕТА РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ

Входное сопротивление RВХ определим из схемы рис.1.24,в:

RBX = R2+R3 .

R2 R3

Искомый ток равен:

Если сопротивление ветви ав (рис.1.22,а) равно нулю (режим короткого замыкания), то протекающий по ней ток является током короткого замыкания IK. Из (1.20) при R=0 входное сопротивление равно:

Из (1.21) следует простой метод экспериментального определения входного сопротивления активного двухполюсника (метод холостого хода и короткого замыкания).

1.12. Условие передачи максимальной мощности приемнику

Рассмотрим простейшую цепь, состоящую из источника ЭДС с внутренним сопротивлением Rвт и приемника с сопротивлением R (рис.1.5,б).

В соответствии с уравнением баланса мощностей:

НАУЧНО-ИНФОРМАЦИОННЫЙ ЦЕНТР САНКТ-ПЕТЕРБУРГСКОГО ГОСУДАРСТВЕННОГО ТЕХНОЛОГИЧЕСКОГО УНИВЕРСИТЕТА РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ

зависимость Р2(I) при изменении тока от нуля до тока короткого замыкания IК (R=0) за счет изменения величины сопротивления R имеет максимум.

Для определения тока I, при котором мощность Р2 имеет максимум, найдем производную от Р2 по I из уравнения (1.22) и приравняем ее к нулю:

Следовательно, при указанном токе мощность Р2 действительно имеет максимум.

Так как сопротивление цепи равно RВТ + R , то при передаче в нагрузку максимальной мощности получим:

Таким образом, приемник потребляет максимальную мощность, если R = RВТ ; такой режим цепи называется согласованным.

Максимальная мощность в нагрузке равна:

Коэффициент полезного действия в согласованном режиме равен:

где I = E 2R.

1.13. Примеры решения задач

1.13.1. Расчет цепей методами преобразования

Задача

Определить токи и напряжения на отдельных участках схемы

(рис.1.25), если U=240 B, R1=R2=0,5 Ом, R3=R5=10 Ом, R4=R6=R7=5 Ом.

27

НАУЧНО-ИНФОРМАЦИОННЫЙ ЦЕНТР САНКТ-ПЕТЕРБУРГСКОГО ГОСУДАРСТВЕННОГО ТЕХНОЛОГИЧЕСКОГО УНИВЕРСИТЕТА РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ

Рис.1.25. Схема для расчета токов методом преобразования

Путем постепенного упрощения найдем эквивалентное сопротивление RЭ схемы, что позволит определить ток I1. Преобразование начинаем с конца схемы:

R67 = R6 + R7 = 5 +5 =10 Ом,

Rвса = R4 + Rвс = 5 +5 =10 Ом.

После указанных преобразований схема имеет вид, показанный на рис.1.26. Найдем эквивалентное сопротивление схемы:

Rэ = R1 + Rва + R2 = 0,5 +5 +0,5 = 6 Ом.

Рис.1.26. Упрощенная исходная схема

Ток в неразветвленной части цепи рассчитывается по закону Ома:

28

НАУЧНО-ИНФОРМАЦИОННЫЙ ЦЕНТР САНКТ-ПЕТЕРБУРГСКОГО ГОСУДАРСТВЕННОГО ТЕХНОЛОГИЧЕСКОГО УНИВЕРСИТЕТА РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ

I = U = 240 = 40 А.

RЭ 6

Токи I3 и I4:

I4 = I1 − I3 = 40 − 20 = 20 А.

Uва =U − I1 (R1 + R2 ) = 240 −40(0,5 +0,5) = 200 В.

Ток I4 является общим для параллельных ветвей R5 и R67 (рис.1.25), поэтому:

I6 = I4 − I5 = 20 −10 =10 А.

Напряжения:

Uвс = I5 R5 =10 10 =100 В,

Uса = I4 R4 = 20 5 =100 В.

1.13.2. Расчет цепей по законам Кирхгофа. Баланс мощностей

Задача

Определить токи в ветвях схемы (рис.1.27), если R1=12 Ом; R2=5 Ом;

R3=2 Ом; R4=4 Ом; R5=4 Ом; R6=1 Ом; R7=24 Ом; Е1=4 В; Е2=1 В; Е6=5 В; Е7=2 В; J2=0,7 A.

Определим число уравнений, которые необходимо составить по законам Кирхгофа:

по 1-му закону n-1=5-1=4,

по 2-му закону m-n+1-q=8-5+1-1=3.

29