8.3. Метод Эйлера

Дано дифференциальное уравнение с начальным условием . Необходимо найти таблицу значений функции на отрезке методом Эйлера.

Рассмотрим графическую интерпретацию метода. Разобьем отрезок на n частей с шагом , причем шаг h должен быть достаточно малым, построим систему равноотстоящих точек . – искомая интегральная кривая. Так как уравнение представляет собой выражение производной , а геометрический смысл производной – тангенс угла наклона касательной, то вместо искомой интегральной кривой рассмотрим касательную к ней в точке . Видно, что значение y₁ можно найти, добавив к y₀ приращение ∆y=LP. LP – катет в прямоугольном треугольнике KLP, его длину можно найти по формуле . Тогда формула для нахождения y₁ примет вид: .

Пользуясь теми же рассуждениями, зная значение y₁, можно найти значения y₂, а затем и все последующие значения функции.

В общем виде формула Эйлера имеет вид:

(5)

Метод Эйлера обладает малой точностью, к тому же погрешность каждого нового шага возрастает. Наиболее удобным на практике является модификация метода Эйлера, в данном случае способ двойного счета с шагом h и с шагом . Если расхождение полученных значений не превышает допустимой погрешности, то шаг для данного этапа выбран правильно, в противном случае шаг уменьшается в два раза.

Совпадение десятичных знаков в полученных двумя способами результатах дает естественные основания считать их верными.

8.4. Метод Рунге-Кутта

Дано дифференциальное уравнение с начальным условием . Необходимо найти таблицу значений функции на отрезке методом Рунге-Кутта.

Метод Рунге-Кутта является более точным, точность достигается за счет усложнения формулы. В общем виде формула метода выглядит так же, как и в методе Эйлера: , но приращение вычисляется иначе.

Разобьем отрезок на n частей с шагом , построим систему равноотстоящих точек .

Рассмотрим числа:

(6)

Приращение ∆y_i будет равно

(7)

Следующее приближение вычисляем по формуле

(8)

Заметим, что шаг расчета можно менять при переходе от одной точки к другой. Для контроля правильности выбора шага h рекомендуется вычитать дробь

(9)

Величина Θ не должна превышать нескольких сотых. В противном случае шаг h следует уменьшить. Точность метода Рунге-Кутта оценивается следующим образом: .

Вообще же метод обладает значительной точностью и широко используется при решении дифференциальных уравнений.

8.5. Метод прогноза и коррекции

В методах Эйлера и Рунге-Кутта при вычислении следующей точки (x_i+1, y_i+1) используется информация только о точке (x_i, y_i), но не о предыдущих точках. И так как эта информация не используется, а также поскольку для метода Рунге-Кутта отсутствуют достаточно простые способы оценки ошибки (погрешности), то целесообразно рассмотреть некоторые дополнительные методы решения дифференциальных уравнений.

В методах прогноза-коррекции, как ясно из названия вначале «предсказывается» значение y_i+1, а затем используется тот или иной метод для «корректировки» этого значения. После этого можно использовать формулу коррекции для вторичной «корректировки» того же значения y_i+1. Этот итерационный процесс можно повторять сколько угодно раз, но для эффективности желательно уменьшить число итераций, выбирая шаг интегрирования.

Существует целый ряд методов прогноза и коррекции – метод Адамса, метод Милна и т.д. Отличаются методы количеством точек, опираясь на которые получают последующую точку.

Рассмотрим наиболее простой метод прогноза и коррекции для решения задачи Коши первого порядка.

Дано дифференциальное уравнение с начальным условием . Необходимо найти таблицу значений функции на отрезке методом прогноза и коррекции.

Разобьем отрезок на n частей с шагом , построим систему равноотстоящих точек .

Формула прогноза.

Так как для предсказания последующей точки необходимо опираться на несколько предыдущих точек, а в задаче Коши дается только одно начальное значение, то еще одно значение найдем, воспользовавшись другим методом, например, методом Рунге-Кутта, т.к. он точнее метода Эйлера. Таким образом, у нас имеются две начальные точки: (x₀, y₀) и (x₁, y₁).

Геометрически предсказание сводится к следующему:

1) В точке проводим касательную L₁.

2) Через точку проводим прямую L, параллельно L.

3) Будем полагать, что предсказанное значение будет расположено там, где прямая L пересечется с прямой .

Рассмотрим треугольник ABC. Значение можно получить, добавив к y₀ приращение . Найдем ВС: так как прямые L и L₁ параллельны, то тангенс угла наклона у них одинаковый, следовательно, .

Таким образом,

Теперь необходимо скорректировать предсказанное значение.

Формула коррекции

1) L₁ – та же самая.

2) Т.к. y₂ приближенно известно, то можно вычислить наклон касательной в точке – касательная L₂.

3) Усредняем тангенсы L₁ и L₂ (биссектриса), получим прямую .

4) Через проводим прямую L, параллельную прямой , получим новое приближение: .

Вычислить это скорректированное значение можно по формуле:

Можно попытаться найти новое, еще лучшее приближение , скорректировав его еще несколько раз. Полагают, что значение функции найдено с необходимой точностью, если .

Далее будем предсказывать и корректировать значение функции в точках x₃, x₄,…, x_n=b.

В общем виде формулы прогноза и коррекции выглядят так:

		(9)
		(10)

Метод прогноза и коррекции сходится к некоторому определенному значению, но не обязательно к точному решению уравнения.

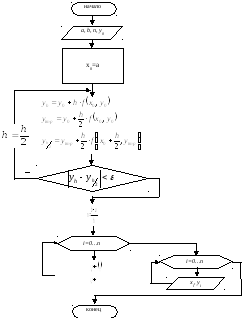
Блок-схема метода