Глава 8. Решение обыкновенных дифференциальных уравнений

8.1. Введение

Во многих областях прикладной математики возникают уравнения, содержащие производную функцию одной переменной. Например, в ситуациях, где рассматривается степень изменения одной переменной по отношению к другой переменной. Такая ситуация описывается дифференциальным уравнением и встречается весьма часто.

● Обыкновенным дифференциальным уравнением называют уравнение, в которое входит функция, зависящая от одной переменной, вместе с несколькими своими производными.

(1)

В зависимости от номера старшей производной, входящей в уравнение, определяют порядок уравнения: дифференциальные уравнения первого порядка, дифференциальные второго порядка и т.д.

Решить дифференциальное уравнение – значит найти функцию, входящую в уравнение.

Различают аналитические и численные методы решения. При аналитическом решении уравнения, находят, соответственно, аналитическое выражение функции, а при численном решении – получают таблицу значений функции на некотором отрезке (в некоторой области).

Существует множество приемов для нахождения решений дифференциальных уравнений через элементарные или через специальные функции. Классические методы решения дифференциальных уравнений на практике очень часто или вообще неприменимы, либо приводят к таким сложным решениям, что затраты труда на их получение или на соответствующие расчеты превосходят все допустимые пределы. В таких случаях решить дифференциальное уравнение можно только численными методами.

Р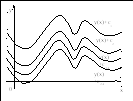ассмотрим, что представляет собой решение дифференциального уравнения графически. Аналитическое выражение искомой функции будет содержать некоторую константу c (постоянную интегрирования), в зависимости от значения которой, интегральная кривая, соответствующая искомой функции будет смещаться вдоль оси Оу. Таким образом, графическое решение дифференциального уравнения – семейство интегральных кривых.

При различных значениях константы c, искомая функция будет принимать в одной и той же точке различные значения. В связи с этим, численное решение дифференциальных уравнений требует дополнительных условий.

Если в дополнении к дифференциальному уравнению задать значение y для некоторого значения x, то можно однозначно определить постоянную c. В зависимости от накладываемых на искомую функцию условий, различают и задачи численного решения дифференциальных уравнений: задача Коши, краевая задача.

8.2. Задача Коши Постановка задачи

Дано дифференциальное уравнение и начальные условия . Необходимо найти функцию y(x), обращающую данное уравнение в верное равенство, и удовлетворяющую начальным условиям.

Простейшим дифференциальным уравнением является уравнение первого порядка:

(2)

Задача Коши для уравнения (2) будет звучать так: найти решение уравнения (2) в виде функции y(x), удовлетворяющей начальному условию:

(3)

Существование и единственность решения уравнения (2) обеспечиваются теоремой:

Теорема Пикара. Если функция f определена и непрерывна в некоторой области G определяемой равенствами:

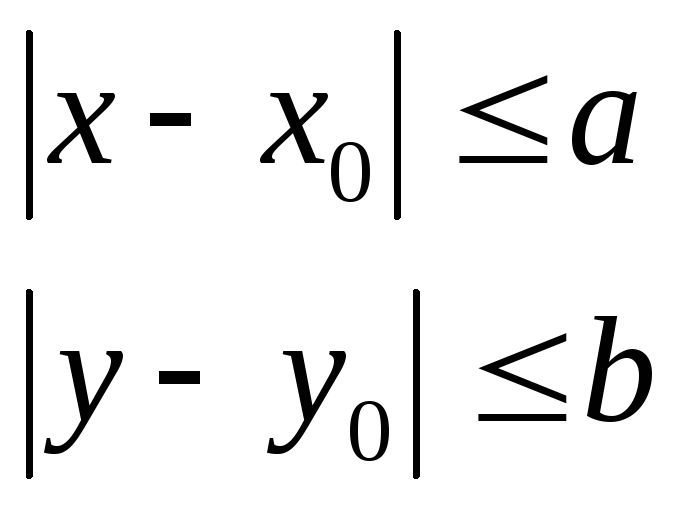
(4)

и удовлетворяет в этой области условию Липшица по y: , то на некотором отрезке , где h – положительное число, существует и притом только одно решение y=y(x) уравнения (2), удовлетворяющее условию (3).

Здесь М – постоянна (константа Липшица), зависящая в общем случае от a и b. Если f(x,y) имеет ограниченную в G производную, то при можно принять .

Геометрический поиск решения уравнения (2) в виде функции y(x), удовлетворяющей условию (3) означает, что требуется найти интегральную кривую y=y(x), проходящую через заданную точку при выполнении равенства (3).

Решение уравнений высших порядков можно свести к решению системы уравнений первого порядка. Например, уравнение второго порядка можно записать в виде системы двух уравнений первого порядка:

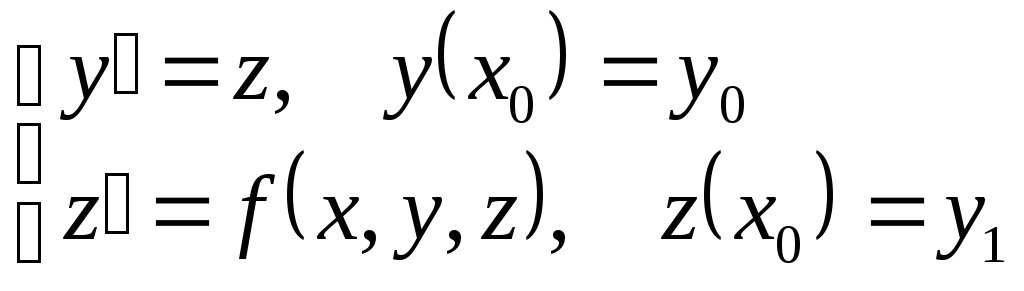
В зависимости от представления решения, методы условно подразделяются на три основные группы:

1 Аналитические методы, применения которых дает решение дифференциального уравнения в виде аналитического выражения.

2 Графические методы, дающие приближенное решение в виде графика.

3 Численные методы, когда искомая функция получается в виде таблицы.