Глава 10. Численные методы решения дифференциальных уравнений с частными производными

10.1. Классификация дифференциальных уравнений с частными производными

В общем случае дифференциальное уравнение с частными производными имеет вид:

(1)

Где xиy– независимые переменные,z– искомая функция,– первые и вторые частные производные по аргументамxиy.

Решением уравнения (1) называется функция , обращающая это уравнение в тождество. График решения представляет собой поверхность в пространствеOxyz.

Уравнение (1) называетсялинейным, если оно первой степени относительно искомой функции и всех ее производных и не содержит их произведений, т.е. если это уравнение может быть записано в виде:

(2)

Причем коэффициенты могут зависеть лишь отxиy. В частности, если эти коэффициенты не зависят отxиy, то уравнение (2) представляет собойлинейное дифференциальное уравнение с постоянными коэффициентами. Остановимся на этом случае подробнее.

Пусть – дискриминант уравнения. В зависимости от знака функцииDлинейное дифференциальное уравнение (2) относится в данной области к одному из следующих типов:

D<0– эллиптический тип

D=0– параболический тип

D>0– гиперболический тип

Если Dне сохраняет постоянного значка – то уравнение будет смешанного типа.

10.2. Метод сеток

Метод сетокилиметод конечных разностей, является одним из самых распространенных методов численного решения дифференциальных уравнений с частными производными.

В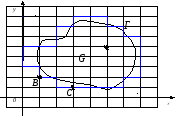основе метода лежит идея замены производных конечно-разностными отношениями. Ограничимся случаем двух независимых переменных.

Пусть в плоскости 0xyимеется некоторая областьGс границейГ. Построим на плоскости два семейства параллельных прямыхи

.

Точки пересечения этих прямых назовем узлами.

● Два узла называются соседними, если они удалены друг от друга в направлении оси0xили0yна расстояние, равное шагу сеткиhилиlсоответственно.

Выделим узлы, принадлежащие области G+Г, а также некоторые узлы, не принадлежащие этой области, но расположенные на расстоянии, меньшем, чем шаг от границыГ.

● Те узлы, у которых все четыре соседних узла принадлежат выделенному множеству узлов, называются внутренними(например, узелА). Оставшиеся из выделенных узлов называютсяграничными(например, узлыВиС).

Значения искомой функции в узлах сетки будем обозначать через.

В каждом внутреннем узле заменим частные производные разностными отношениями:

,

(3)

В граничных точках будем пользоваться менее точными формулами:

,

(4)

Аналогично заменяем производные второго порядка:

,

(5)

Указанные замены производных в каждом узле сетки позволяют свести решение дифференциальных уравнений с частными производными к решению системы разностных уравнений.

10.3. Итерационные методы решения системы конечно-разностных уравнений

В некоторых случаях требуется решить дифференциальное уравнение с частными производными с заданной точностью. Одним из наиболее простых методов является процесс усреднения Либмана.

Согласно этому методу вычисления ведутся следующим образом: вначале вычисляются (находятся) начальные приближения значений искомой функции, а затем последовательнее приближения для внутренних узлов определяются по формуле:

(6)

Начальные приближения значений функции во внутренних точках можно получить следующими способами:

• путем интерполяции, используя известные граничные значения;

• составляют систему конечно-разностных уравнений для сетки с более крупным шагом, а затем полученные значения интерполируют на узлы даннойсетки.

Если границаГобластиGкриволинейна, то значения искомой функциидляграничных узловполучают путем переноса значений из точек на границеГ. Погрешность, получающуюся в результате такого переноса можно значительно уменьшить, если для каждого граничного узла составить уравнения следующего вида:

для узлаA_h

для узлаD_h,

где A_hиD_h– узловые граничные точки,АиD– ближайшие кA_hиD_hточки, лежащие на границе, δ₁и δ₂– расстояния междуAиA_h, иDиD_hсоответственно, причем, со знаком «+», если точка внутри области, и знаком «–», если точка вне области.

Пересчет граничных значений методом Либмана проводится по формулам:

(7)

Итерации продолжают до тех пор, пока в двух последовательных приближениях значений функции, причем, как во внутренних, так и в граничных точках не совпадут требуемое количество десятичных знаков, т.е. .