Динамический хаос (ИПИС, ФКС)

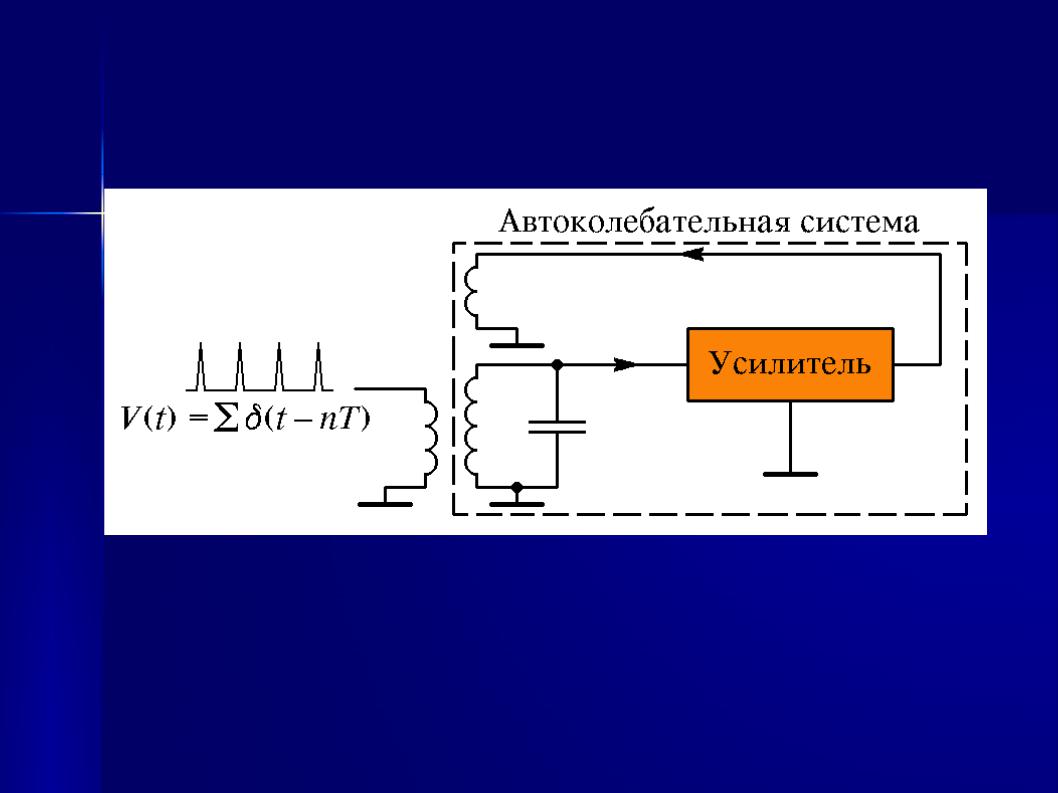
Рис. 83. Автоколебательная система под периодическим воздействием.

Процесс увеличения амплитуды колебаний будет продолжаться до тех пор, пока энергия, поставляемая в контур за период колебаний, не сравняется с энергией, теряемой системой на нагрев за тоже время. С этого момента амплитуда колебаний перестанет изменяться с течением времени, и в контуре возникнут незатухающие колебания с некоторой постоянной частотой 0 и амплитудой a0 . Такие самоподдерживаемые колебания называются автоколебаниями. При этом в фазовом пространстве системы такому установившемуся режиму автоколебаний будет соответствовать аттрактор в виде предельного цикла (см., например, рис. 5).

Рис. 5. Фазовые траектории автоколебательных систем.

Пусть теперь на эту систему действуют периодические импульсы напряжения с периодом T (см. рис. 83). Эти импульсы будут выводить систему из установившегося режима движения, изменяя скачком амплитуду колебаний:

постепенно возвращаться к исходному предельному циклу, в

где – коэффициент затухания возмущения амплитуды, характеризующий скорость релаксации к предельному циклу.

Т.к. автоколебательные системы в общем случае нелинейны, то

где – фаза колебаний, – некоторый постоянный коэффициент, определяющий влияние изменения амплитуды на частоту колебаний.

Пусть перед очередным n -м толчком отклонение амплитуды от предельного цикла было равно rn , а фаза равнялась n . Как было сказано ранее, в результате воздействия импульса возникает некоторая добавка к амплитуде, которая должна быть некоторой периодической функцией фазы n в этот момент. В самом простом случае в качестве такой функции можно выбрать, например, функцию синус. Тогда сразу после воздействия импульса имеем:

где A – параметр, характеризующий интенсивность импульсов. Тогда, используя уравнения (182) и (183), можем определить значения величин r и спустя время T , т.е. в момент перед началом действия (n 1) -го импульса:

rn 1 rn exp( T ) (rn Asin n ) exp( T ) , (185)

n 1 n 0T rn 1 exp( T )

n 0T (rn Asin n ) 1 exp( T ) . (186)

Вводя новые обозначения

exp( T ) 1 r ,

dexp( T ) ,

0T ,

преобразования (185) и (186) можно переписать в виде

Преобразования (188) называют отображением Заславского. Оно представляет собой двумерное отображение для пары величин ( n , n ) , при этом, т.к. является фазой, то её значения, отличающиеся друг от друга на 2 m , следует считать эквивалентными.