Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северный (Арктический) федеральный университет им. М. В. Ломоносова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

К р 3,4 ПЭ спецглавы 3 сем 2012

.pdf

Скачиваний:

Добавлен:

13.02.2015

Размер:

515.3 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Министерство образования и науки РФ Северный Арктический федеральный университет им. М.В.Ломоносова

Кафедра математики

Вопросы по курсу спецглавы математики

3 семестр

для студентов 2 курса заочной формы обучения ИЭиТ направление подготовки 140100.62 «Теплоэнергетика и теплотехника»

Функция нескольких переменных.

1.Функции нескольких переменных (ФНП). Область определения, предел и непрерывность ФНП.

2.Производные и дифференциалы ФНП. Геометрический смысл частных производных. Нормаль и касательная плоскость к поверхности. Производная по направлению ФНП и градиент.

3.Производные и дифференциалы высших порядков. Экстремум ФНП. Наибольшее и наименьшее значения ФНП в замкнутой области.

Дифференциальные уравнения.

4.Основные понятия теории обыкновенных дифференциальных уравнений (ДУ). Задачи, приводящие к ДУ. Общее и частное решения ДУ. Задача Коши для ДУ 1-го порядка.

5.ДУ с разделяющимися переменными, однородные, линейные, уравнения Бернулли.

6.Задача Коши для ДУ 2-го порядка. ДУ второго порядка, приводящиеся к ДУ 1-го порядка.

7.Линейные ДУ второго порядка. Свойства их решений. Характеристическое уравнение. Структура общего решения неоднородного ДУ второго порядка.

8.Метод вариации произвольных постоянных для решения линейных уравнений 2-го порядка.

9.Системы дифференциальных уравнений. Линейные однородные системы ДУ с постоянными коэффициентами. Приведение системы ДУ к обыкновенному ДУ.

Ряды.

10.Числовой ряд и его сумма. Необходимое условие сходимости ряда. Достаточные признаки сходимости знакоположительных числовых рядов: признаки сравнения, признак Даламбера, радикальный и интегральный признаки Коши.

11.Знакопеременные ряды. Абсолютная и условная сходимость знакопеременных числовых рядов. Знакочередующиеся ряды. Теорема Лейбница.

12.Функциональные ряды, сумма ряда и область сходимости. Степенные ряды. Теорема Абеля. Радиус и интервал сходимости степенного ряда. Ряды Тейлора. Разложение основных элементарных функций в ряд Тейлора. Приложения степенных рядов.

13.Тригонометрический ряд Фурье. Теорема Дирихле. Ряд Фурье для 2 - периодической функции и для функций с произвольным периодом.

Кратные интегралы.

14.Двойной интеграл: определение, свойства. Геометрический смысл двойного интеграла. Вычисление двойного интеграла в декартовых координатах.

15.Замена переменных в двойном интеграле. Якобиан и его геометрический смысл. Переход в двойном интеграле от декартовых координат к полярным.

16.Приложения двойного интеграла: вычисление площади плоской фигуры, объемов тел, масс плоской фигуры, статических моментов и координат центра тяжести плоской фигуры.

17.Тройной интеграл: определение, свойства. Вычисление тройного интеграла в декартовых координатах. Замена переменных в тройном интеграле. Переход в тройном интеграле от декартовых координат к цилиндрическим и сферическим.

18.Приложения тройного интеграла: вычисление объемов тел, массы тел, статических моменты и координат центра тяжести трехмерных тел, моментов инерции.

Теория вероятностей и математическая статистика.

19.Элементы комбинаторики. Перестановки, размещения и сочетания. Случайные события. Алгебра событий.

20.Классическое определение вероятности. Частота и вероятность появления события. Геометрическое определение вероятности. Теоремы сложения и умножения. Условная вероятность. Независимость событий. Формула полной вероятности и формулы Байеса.

21.Повторные испытания. Формула Бернулли. Формула Пуассона. Локальная и интегральная теоремы Лапласа.

22.Случайные величины (СВ): дискретные и непрерывные. Законы распределения и числовые характеристики СВ. Основные законы распределения случайных величин: закон Пуассона, биномиальный, геометрический, равномерный, показательный и нормальный. Правило трёх сигм. Закон больших чисел.

23.Системы СВ. Законы распределения и числовые характеристики систем СВ. Нормальный закон на плоскости.

24.Функции случайных величин. Числовые характеристики и закон распределения функции СВ.

25.Задачи математической статистики. Генеральная совокупность и выборка. Эмпирические и теоретические частоты. Эмпирическая функция распределения. Числовые характеристики статистического распределения.

26.Проверка статистических гипотез. Ошибки 1-го и 2-го родов. Критерии согласия Пирсона, Колмогорова. Точечные и интервальные оценки параметров распределения.

27.Понятие о регрессионном и корреляционном анализе. Линейная регрессия. Построение регрессионной прямой по сгруппированным данным. Линейная корреляция. Коэффициент корреляции, его свойства. Проверка гипотезы о значимости коэффициента корреляции.

Литература

1.Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. – М.: Наука, 1980, 1984.

2.Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. –

М.: Наука, 1981, 1985.

3.Бугров Я.С., Никольский С.М. Высшая математика. Задачник.– М.: Наука, 1982.

4.Данко П. Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: в 2-х ч, Ч.1 - 6-е изд. - М.: ОНИКС: Мир и Образование, 2003. - 304 с.

5.В.Е. Гмурман «Руководство к решению задач по теории вероятностей и математической статистике.»; М., Высшая школа, 1998, 400 с.

6. Н.С. Пискунов	«Дифференциальное и интегральное исчисление.»	.
т.1, 2; М., Наука, 1985.

7.Письменный, Д. Т. Конспект лекций по высшей математике. - М.: Айрис-пресс, 2010. - 288 с.,часть I.

8.Письменный, Д. Т. Конспект лекций по высшей математике. - М.: Айрис-пресс, 2010. - 256 с., часть II.

9.Щипачев В.С. Высшая математика. – М.: Высшая школа, 1990.

10.Чистяков В.П. Курс теории вероятностей. – М.: Наука, 1982.

11.Калинина В.Н., Панкин В.Ф. Математическая статистика. – М.: Высшая школа, 1994.

3.2.2 Дополнительные источники: методические указания кафедры математики.

1. Ряды: метод. указания к выполнению расчет.-графич. (контрол.) работы / сост. О.А. Хотенова. – Архангельск: Арханг. гос. техн. ун-т, 2010. – 54 с.

http://narfu.ru/imikt/depart/maths/education/books/Ryady%20Hotenova.pdf

2. Теория вероятностей и математическая статистика: учебное пособие / сост. Л. А. Баданина, Г.В. Серова. Архангельск: САФУ, 2011. – 89 с.

http://www.narfu.ru/university/library/elib.php#б

3. КримнусЕ. А. Случайные события: метод.указ.к выполнению самостоятельной работы / Е. А. Кримнус, Н. А. Шиловская.- Архангельск: С(А)ФУ, 2010. — 67 с.

http://www.narfu.ru/university/library/elib.php#б

Интернет ресурсы: http://www.exponenta.ru/

Контрольная работа № 3

Функции нескольких переменных. Дифференциальные уравнения. Ряды. Кратные интегралы.

Задание 1. Даны функция z(x; y), точка A(x0; y0 ) и вектор a. Найти: a) градиент функции z(x; y) в точке A;

б) уравнение касательной плоскости в точке A к поверхности, заданной уравнением z z(x; y);

в) производную функции z(x; y) в точке A по направлению вектора a.

1.1.z ln(3x2 2y2 );

1.2.z x2 5y;

1.3. z arccos		x		;

	2y
1.4. z e2x2 4xy ;
1.5. z arcsin	x		;

		y

1.6.z ln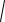4 x2 y2 ;

1.7.z arctg x2 ;

1.8.z 3x y2 ;

1.9.z ln(3x 2y)2;

1.10. z		4	;
	x2	y2

A( 1; 2),

A(2; 2),

A(2;1),

A(1; 4),

A(1; 1),

A( 2; 4),

A(1; 2),

A(2;1),

A( 2; 2),

a 3i 4 j .

a 2i 5j.

a 8i 6j.

a 3i 4 j .

a 5i 12j.

a i j .

a 4i 3j .

a 2i j .

a 2i 2 j.

a 6i 8j.

Задание 2. Дана функция z(x; y), исследовать ее на экстремум.

2.1. z xy x2 2y2 x 10y 8.		2.4. z 3x2 3y2 5xy 4x 7y 5.
2.2. z 3x2 3xy y2	6x 2y 1.	2.5. z 3xy x2	3y2 6x 9y 4.
2.3. z 3xy x2 4y2	4x 6y 1.	2.6. z x2 y2	3xy x 4y 1.
		4

2.7.	z x2 y2 xy x y 2.	2.9. z x2 2xy y2 6x 10y 1.
2.8.	z 3x2 3y2 5xy x y 5.	2.10. z 4 5x2 4xy y2 4x 2y.

Задание 3. Изменить порядок интегрирования в интеграле. Область интегрирования изобразить на чертеже.

	1			3 x			4			25 x2
3.1.	dx			f (x, у)dy		3.6.		dy						f (x, у)dx
3.1.	0			2x	2	3.6.
	0			2x			0				3x
										4
		3							4
		3		у 3			4		4			x
3.2.	2			у 3		3.7.	dx			f (x, у)dy
3.2.	dу f (x, у)dx					3.7.	dx			f (x, у)dy
	dу f (x, у)dx						0			х2
	0			2у2
	0			2у2						2
										2
	0			x 3			2		2 y
3.3.		dx f (x, у)dy				3.8.	dy			f x, y dx
	1			2x2			0		y	2		1
									4			1
									4
	1			3 y			1		x2 1
3.4.	dy			f (x, у)dx		3.9.	dx			f (x, у)dy
	0			2y2			0		1
	0			3 x
	0			3 x			4			25 y2
3.5.		dx f (x, у)dy				3.10.		dy						f (x, у)dx
3.5.	3			2x2		3.10.
							0					3	y
			2									3
			2							4
										4

Задание 4. Вычислить объём тела, ограниченного указанными поверхностями. Данное тело и область интегрирования изобразить на чертеже.

4.1. z 0, z 2x, x y 3, х у . 2

4.2.x 0, y 0, z 0, x y 2, у 1 z .

4.3.z 0, z 1 x2 , y 0, y 3 x.

4.4.z 0, z 1 y, y x2 .

4.5. z 0, z 2 x, x 1, x y2 .

4.6.	x 0,	y 0,		z 0,			x y	1, z x2	3y2 .
4.7.	x 0,	y 0,		z 0,			x 1,	x y 2,	z x2	1	y2 .

									2
4.8.	x 0,	y 0,		z 0,			y z 1, x y2		1.
4.9.	z 0,	z 1 y2 ,				x y2 ,		x 2y2 1.
4.10.	z 0,	z			,	y x2 .
			1 y

Задание 5. Найти общее решение дифференциального уравнения первого порядка.

5.1.

(2x y)dx (x y)dy 0.

5.6.

y x y

5.2.

(x2 y2 )dx 2xydy 0

5.7.

y 2xy xe x2

5.3.

y e

5.8.

y 3x2 y x2

5.4.

5.9.

xy y 3 0

xdy ydx

x2 y2 dx

5.5.

x y

5.10.

x2 0

x y

1 x

Задание 6. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям.

6.1.

5y xe

;

y(0)

y (0)

6.2.

;

y(0)

y (0)

6.3.

6y (12x

7)e

;

y(0) 0; y (0)

6.4.

;

y(0)

(0) 0.

6.5.

6y 12cos2x 8sin 2x;

y(0) 1;

y (0) 3.

6.6.

y 2cosx;

y(0) 1;

y (0) 0.

6.7.

9y 10sin x; y(0) 0;

(0) 0.

6.8.

; y(0)

(0) 0.

6.9.

5y 2x

; y(0)

y (0) 3.

6.10.

13y 26x 1;

y(0) 0;

y (0) 1.

Задание 7. Исследовать сходимость рядов (а, б) и найти интервал сходимости (в).

2n 1 n

7.1.

а)

;

б)

n 1

5n 1

7.2.

а)

;

б)

n 1

7.3.

а)

;

б)

n 1

(2n 1)!

6n 1

7.4.

а)

;

б)

n 1

7.5.

а)

;

б)

nlnn

n 1

;

n 1

;

n 1

2n 1

1 n

;

n 1

;

n 1

n 1 !

1 n

;

n 1

n 1 !

(x 1)

в)

n 1

1 n 1 x 5 n

в)

n 1

x 1

в)

n 1

x 1

в)

n 1

x 3

в)

n 1

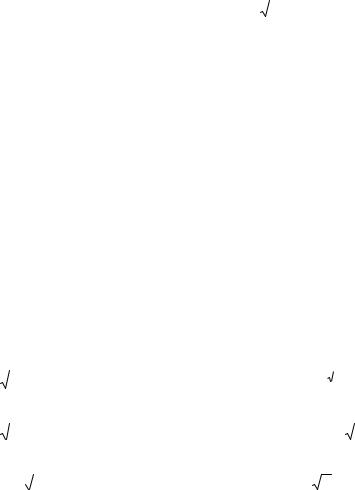
7.6.а)

7.7.а)

7.8.а)

7.9.а)

7.10.а)

Задача 8.

2n 1

;

б)

n 1 n2 n 1

1 n

б)

;

n 1 2 n

n 1!

n 1

б)

5 n

; б)

n 1

;

б)

n 1

2n 1

1 n 1

;

в)

1 n 1 x 5n

n 5

n 1

x 3

1 n 1

;

в)

n 1

n3 n

в)

n5n

;

x 24 .

n 1

n n 1

n 1

2n 1

(x 2)2n

;

в)

n(n 1)

n 1

n n

(x 1)2n

( 1)

;

в)

n 1

2n 1

n 1

Вычислить с точностью до 0,001.

	0.5						0.5		2
8.1.		xe 2xdx.				8.6.		cos			x			dx.
8.1.		xe 2xdx.				8.6.		cos			4			dx.
	0						0
	1							1
	1						3
8.2.	ln 1 x2 dx.					8.7.	3
8.2.	ln 1 x2 dx.					8.7.	sin x2dx.
	0						0
							0
		1						1
8.3.	2					8.8.	4
			1 x3 .				xe					dx.
			1 x3 .				xe			x		dx.
	0						0
	1						1
8.4.			x	sin xdx.		8.9.	xcos						xdx.
	0						0
	1						1
8.5.	cos3					8.10.			xe x2 dx.
8.5.	cos3				xdx.	8.10.			xe x2 dx.
	0						0

Контрольная работа № 4

Теория вероятностей. Математическая статистика

Каждый вариант состоит из восьми заданий на отдельных страницах (см. ниже).

Вариант 1.

из контрольной работы № 4

Теория вероятностей. Математическая статистика

Задача 1. Куб, все грани которого окрашены, распилен на 125 кубиков одинакового размера. Все кубики перемешаны. Найти вероятность того, что кубик, извлечённый на удачу, будет иметь две окрашенные грани.

Задача 2. На склад поступила продукция трёх фабрик, причём продукция первой фабрики составляет 20%, второй - 46%, третьей - 34% всей продукции. Известно также, что средний процент нестандартных изделий для первой фабрики равен 3, для второй - 2, для третьей - 1. Найти вероятность того, что наудачу взятое и оказавшееся нестандартным изделие произведено на первой фабрике.

Задача 3. Вероятность поражения мишени при одном выстреле равна 0,75. Найти вероятность того, что при 12 выстрелах мишень будет поражена:

а) 10 раз; б) не более 10 раз.

Задача 4. Два стрелка сделали по одному выстрелу по мишени. Вероятность попадания в мишень первого стрелка равна 0,6, а для второго – 0,7. Необходимо: а) составить закон распределения случайной величины Х – общего числа попаданий; б) найти математическое ожидание и дисперсию этой случайной величины.

Задача 5. Случайная величина X задана функцией распределения

0,	x 2,
		2 x 3,
F x x 2 2,		2 x 3,
1,	x 3.

Вычислить вероятность попадания случайной величины X в интервалы (1; 2,5)

и (2,5; 3,5). Найти	М X ,D X , X . Построить графики функций F(x), f(x).
Задача 6. Случайная величина X задана дифференциальной функцией
распределения
	f x	1		e	x 1 2
		1			32	.
					32	.
	4		2
По какому	закону	распределена					случайная величина? Найти
М X ,D X , X ,	F х , P 0 X 2 .

Задача 7. Из партии, содержащей большое количество деталей, было отобрано n деталей. Распределение этих деталей по длине дано в таблице. Используя 2-критерий Пирсона, на основе выборочных данных при уровне значимости 0,05 проверить гипотезу о том, что случайная величина X- длина детали распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.

Длина,	3,1	3,2	3,3	3,4	3,5	3,6	3,7
мм

число	3	17	60	122	122	61	15
деталей

Задача 8.

В таблице приведена выборка n видов изделий по затратам сырья X(руб) и цене готовой продукции Y (руб).

Необходимо:

1)вычислить групповые средние xi и yj и построить эмпирические линии регрессии;

2)предполагая, что между переменными x и y существует линейная корреляционная зависимость:

найти уравнения прямых регрессии и построить их графики на том же чертеже, на котором построены эмпирические линии регрессии;

вычислить коэффициент корреляции, оценить его значимость на 5% уровне и сделать вывод о тесноте и направлении связи;

используя соответствующее уравнение регрессии, оценить среднюю цену готовой продукции, если затраты сырья составили xo= 100 руб.

хy 150-170 170-190 190-210 210-230 230-250 250-270 270-290 итого

80-90	3	4	1					8

90-100	2	5	12	9				31

100-110		8	20	28	3			56

110-120			6	20	18	7		51

120-130				15	18	8	5	46

130-140						5	3	8

Итого	5	17	39	72	39	20	8	n=200

Вариант 2.

из контрольной работы № 4

Теория вероятностей. Математическая статистика

Задача 1. В двух коробках смешаны конфеты трёх сортов. В первой коробке 10 конфет одного сорта, 15 другого и 25 третьего, а во второй соответственно 30, 15 и 5. Из коробок берут наудачу по одной конфете. Какова вероятность того, что они одного и того же сорта?

Задача 2. Установлено, что 20% банок импортных мясных консервов и 10% отечественных были низкого качества. В продаже импортные и отечественные консервы представлены в количествах, относящихся как 3:7. Найти вероятность того, что наудачу выбранная банка мясных консервов - хорошего качества.

Задача 3. Вероятность нарушения герметичности банки консервов равна 0.004. Найти вероятность того, что из 500 банок таких консервов герметичность нарушена не менее, чем у трёх банок.

Задача 4. В некотором цехе брак составляет в среднем 6% всех изделий. Составить закон распределения случайной величины X, выражающей число бракованных изделий из 5 взятых наудачу изделий. Найти математическое ожидание и дисперсию этой случайной величины и проверить их значения по формулам этих характеристик для случайной величины, распределённой по биномиальному закону.

Задача 5. Непрерывная случайная величина Х задана функцией распределения

0,				x 3,
	x 3 2
	x 3 2
F x			, 3 x 5,
F x		4	, 3 x 5,
		4		x 5
1,				x 5
	распределения f х ,				М X ,D X , X ,
Найти функцию плотности	распределения f х ,				М X ,D X , X ,
P 1,5 X 4,5 . Построить графики функций F х и				f х .

Задача 6. Чему равна вероятность того, что нормальная случайная величина с математическим ожиданием, равным 3, и дисперсией, равной 1, примет значение из интервала (0,5; 3,5)? Найти выражения для плотности вероятности f х и функции распределения F х .

Задача 7. Из партии, содержащей большое количество деталей, было отобрано n деталей. Распределение этих деталей по длине дано в таблице. Используя 2-критерий Пирсона, на основе выборочных данных при уровне значимости 0,05 проверить гипотезу о том, что случайная величина X – длина детали распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.11.2018400.9 Кб3ИТЗ 1-1.doc
#
09.09.2019316.78 Кб4Итз ОИР.docx
#
08.11.2019462.85 Кб29ИТЗ по философии.doc
#
13.02.2015795.63 Кб4ИТМ Мешанина.docx
#
13.02.201564.24 Кб4Итоговый документ страноведение..docx
#
13.02.2015515.3 Кб15К р 3,4 ПЭ спецглавы 3 сем 2012.pdf
#
13.02.2015364.57 Кб3К р ТВ и МС ИЭиТ, 3 курс 2014, 140400.pdf
#
19.09.201949.03 Кб0к экзамену по госрегистрации.docx
#
11.03.201685.5 Кб16К.Р по английскому языку..doc
#
27.04.2019122.88 Кб1к.р Формальные группы.doc
#
11.03.201640.49 Кб21к.р. детское чтение.docx