
К р ТВ и МС ИЭиТ, 3 курс 2014, 140400
.pdfМинистерство образования и науки РФ Северный (Арктический) федеральный университет Кафедра математики
Вопросы к экзамену по математике
для студентов 3 курса ИЭиТ, 140400, заочной формы обучения
1.Опыт и событие. Классификация событий. Операции над событиями.
2.Основные формулы комбинаторики (перестановки, размещения, сочетания).
3.Классическое, статистическое (относительная частота наступления события) и гео-
метрическое определения вероятности.
4.Пространство элементарных событий. Аксиоматическое определение вероятности.
5.Теоремы сложения для совместных и несовместных событий.
6.Зависимые и независимые события. Теорема умножения для зависимых и независи-
мых событий. Вероятность наступления только одного события. Вероятность насту-
пления хотя бы одного события.
7.Формула полной вероятности.
8.Формулы Байеса.
9.Повторные независимые испытания. Формула Бернулли
10.Повторные независимые испытания. Локальная и интегральная теоремы Лапласа.
11.Повторные независимые испытания. Теорема Пуассона.
12.Дискретные случайные величины. Закон распределения и функция распределения дискретной случайной величины.
13.Непрерывные случайные величины. Функция распределения непрерывной случай-
ной величины. Ее свойства.
14. Непрерывные случайные величины. Плотность распределения непрерывной слу-
чайной величины. Ее свойства.
15. Математическое ожидание дискретной и непрерывной случайной величины. Свой-
ства математического ожидания.
16. Дисперсия дискретной и непрерывной случайной величины. Свойства дисперсии.
Среднеквадратическое отклонение и его свойства.
17. Теоретические моменты случайных величин. Связь центральных и начальных мо-
ментов. Коэффициент асимметрия и коэффициент эксцесса.
18.Биномиальное распределение. Закон распределения. Числовые характеристики.
19.Пуассоновское распределение. Закон распределения. Числовые характеристики.
20.Геометрическое распределение. Закон распределения. Числовые характеристики.
21. Равномерное распределение. Плотность распределения и функция распределения.
Числовые характеристики равномерного распределения.
22. Показательное распределение. Плотность распределения и функция распределения.
Числовые характеристики показательного распределения.
23.Нормальное распределение. Плотность распределения. Числовые характеристики.
24.Двумерные случайные величины: закон распределения двумерной случайной вели-
чины, независимость случайных величин. Числовые характеристики меры связи случайных величин: ковариация, коэффициент корреляции.
25. Закон больших чисел. Неравенство Чебышева. Теорема Маркова. Теорема Чебыше-
ва и устойчивость средних. Теорема Бернулли и устойчивость относительных час-
тот.
26.Генеральная совокупность и выборка. Вариационный ряд.
27.Полигон. Гистограмма. Полигон накопленных относительных частот (кумулята).
Эмпирическая функция распределения.
28. Точечные оценки числовых характеристик генеральной совокупности: средняя вы-
борочная, дисперсия выборочная, S 2 и их свойства: несмещенность, состоятель-
ность, эффективность.
29.Интервальные оценки параметров распределения. Точность оценки, доверительная вероятность (надежность). Доверительный интервал.
30.Проверка статистических гипотез. Критерии согласия (критерий Пирсона).
31.Выборочное уравнение регрессии. Отыскание параметров выборочного уравнения прямой линии регрессии по несгруппированным данным (методом наименьших квадратов).
32.Вычисление коэффициента корреляции по выборочным данным. Оценка тесноты зависимости изучаемых явлений.
Составил: И.Н. Попов
2
Контрольная работа
«Теория вероятностей и математическая статистика»
Задание 1.
1.На 5 карточках написано по одной цифре из набора от 1 до 5. Выбираются одна за другой две карточки. Какова вероятность того, что число на второй карточке боль-
ше, чем на первой?
2.В одном ящике 6 белых и 4 черных шарика, в другом – 7 белых и 3 черных. Из каж-
дого ящика вынимается по одному шарику. Чему равна вероятность того, что оба шарика окажутся белыми?
3.Из группы студентов, в которой 15 юношей и 5 девушек, выбирается команда в со-
ставе 4 человек. Какова вероятность того, что в составе этой команды окажутся двое юношей и две девушки?
4.В одном ящике 8 белых и 5 черных шарика, в другом – 5 белых и 3 черных. Из каж-
дого ящика вынимается по одному шарику. Чему равна вероятность того, что оба шарика окажутся разных цветов?
5.Из коробки, в которой находилось 4 красных и 7 зеленных карандашей, выпало 4 ка-
рандаша. Найдите вероятность того, что 3 из них окажутся зеленными.
6.Из колоды в 36 карт вытаскивают 7 карт. Какова вероятность того, что среди вы-
бранных карт будет не менее 6 карт черной масти?
7.Бросаются две игральные кости. Найдите вероятность того, что выпадет хотя бы од-
на шестерка.
8.Записано произвольное двузначное число. Какова вероятность того, что сумма цифр этого числа окажется равной 6?
9.Задумано шестизначное число, у которого цифра 7 встречается 4 раза, а цифра 3 – 2
раза. Какова вероятность угадать число с первого раза?
10.На книжной полке произвольно расставлены 4 различные книги из серии «Фанта-
стика» и 3 различные книги из серии «Приключения». Какова вероятность того, что
все книги из одной и той же серии окажутся рядом?
3
Задание 2.
Вычислите вероятность, где x, y [0;1].
1.P(1 1 y x). x
2.P(x2 y x 1).
3.P( 1 2 y x 1). x
4.P(x3 y x 1).
5.P( x3 1 y x).
6.P( x2 1 y x).
7.P( x2 1 y x3 1).
8.P(x2 y x3 1).
9.P( 1 2 y x3 1). x
10.P(x2 y 1 2).
x
Задание 3
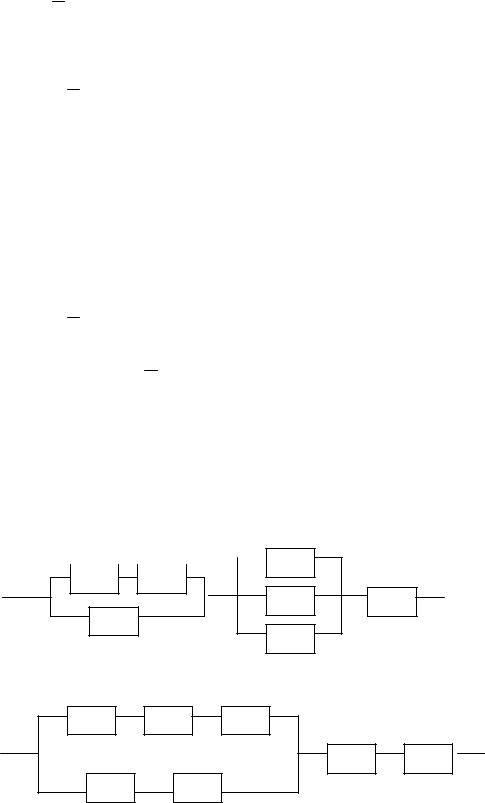
Найти вероятность прохождения тока через цепь, если вероятности исправной работы элементов указаны на схеме. Элементы работают независимо друг от друга.
1.


 0,6 0,9 0,8
0,6 0,9 0,8
0,7 0,7
0,7
0,8
2.
0,7 0,8 0,9
0,7 0,9
0,7 0,8
4
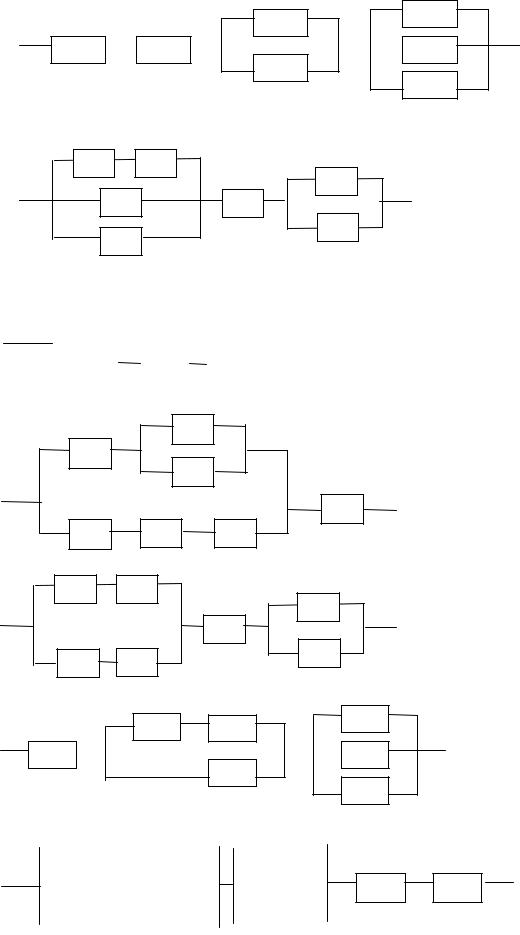
3.
0,8
0,7
0,5 |
|
0,6 |
|
|
|
0,8 |
0,9
0,4
4.
0,4 0,7
0,6
0,8 0,9
0,8
0,9
5.
6.
7.
|
0,9 |
|
0,8 |
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,7 |
|
0,6 |
|
|
|
|
0,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9 |
0,6 |
|
|
|
|
0,8 |
|
|
0,9 |
0,7 |
0,5 |
0,6 |
0,4 |
0,7 |
|
|
|
0,6 |
|
|
0,9 |
0,9 |
0,8 |
0,8 |
|
8.
0,8
0,6 0,7
0,5 |
|
|
|
0,8 |
0,9
0,4
9.
|
|
|
|
|
|
|
0,9 |
|
|
0,7 |
|
0,8 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,7 0,9
|
0,7 |
|
|
|
0,8 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
5
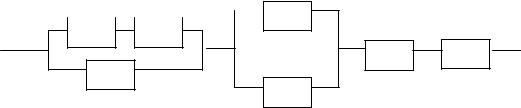
10.


 0,6 0,9 0,8
0,6 0,9 0,8
0,7 0,7
0,7
0,8
Задание 4
1.Имеется 4 прибора, вероятность каждого из них оказаться исправным, равна 0,4. Найти вероятность исправности: а) трех приборов; б) хотя бы одного прибора; в) не менее трех приборов.
2.Стрелок производит три независимых выстрела с вероятностью попадания в цель 0,2. Найти вероятность: а) двух попаданий; б) трех промахов; в) хотя бы одного попадания; г) не менее двух попаданий.
3.Студенту задано три вопроса, вероятность ответить на каждый из них равна 0,8. Найти вероятность того, что студент ответит: а) на два вопроса; б) не менее чем на два вопроса; в) хотя бы на один вопрос.
4.Число вызовов, поступающих на АТС, подчинено закону Пуассона со средним числом вызовов в минуту равным двум. Найти вероятность того, что в минуту поступит: а) три вызова; б) не менее трех вызовов; в) не более трех вызовов.
5.Автоматическая линия выпускает 1000 деталей в час с вероятностью выпуска бракованной детали 0,002. Найти вероятность изготовления: а) пяти бракованных деталей в час; б) не менее пяти бракованных деталей в час; в) не более пяти бракованных деталей в час.
6.По цели производится три независимых выстрела. Вероятность попадания при одном выстреле равна 0,4. Для поражения цели достаточно двух попаданий. При одном попадании цель практически не поражается. Найти: а) вероятность поражения цели; б) вероятность того, что в цель не будет ни одного попадания.
7.Завод отправил потребителю партию из пятисот изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что потребитель получит менее трех негодных изделий.
8.В мастерской имеется 10 моторов. При существующем режиме работы вероятность того, что мотор в данный момент работает с полной нагрузкой, равна 0,8. Найти вероятность того, что в данный момент не менее 8 моторов работает с полной нагрузкой.
9.Вероятность появления бракованной детали, изготовленной станком-автоматом, равна 0,01. Найти вероятность того, что среди 200 деталей, изготовленных этим станком, будет: а) четыре бракованные детали; б) более четырех бракованных деталей.
10.Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится семь независимых выстрелов. Найти вероятность того, что будет не менее двух попаданий.
6
Задание 5
Дискретная случайная величина Х задана рядом распределения.
1. |
|
Xi |
|
-1 |
|
0 |
|
1 |
|
2 |
|
|
Pi |
|
0,1 |
|
0,2 |
|
P3 |
|
0,3 |
|
Найти: |
P3; М(Х); D(X); P(x < 2); F(x). |
|
|||||||
2. |
|
Xi |
|
-20 |
|
0 |
|
40 |
|
|
|
|
|
|
|
|
|||||
|
|
Pi |
|
0,2 |
|
P2 |
|
0,5 |
|
|
|
Найти: |
P2; М(Х); D(X); P(0 x ); F(x). |
|
|||||||
3. |
|
Xi |
|
0 |
|
1 |
|
2 |
|
5 |
|
|
|
|
|
||||||
|
|
Pi |
|
0,1 |
|
0,2 |
|
0,4 |
|
P4 |
|
|
Найти: |
P4; М(Х); D(X); P(0 x < 3 ); F(x). |
|
||||||
4. |
|
Xi |
|
-2 |
|
x2 |
|
2 |
|
|
|
|
|
|
|
|
|||||
|
|
Pi |
|
0,2 |
|
0,3 |
|
P3 |
|
|
Известно, что М(Х) = 0,6. Найти: P3; x2; D(X); P(-1 x < 2 ); F(x).
5. |
Xi |
-10 |
0 |
10 |
20 |
|
Pi |
0,1 |
P2 |
0,2 |
0,5 |
Найти: P2; М(Х); D(X); P(0 x < 15 ); F(x).
6. |
Xi |
0 |
x2 |
3 |
|
Pi |
0,1 |
0,4 |
P3 |
Известно, что М(Х) = 1,9. Найти: P3; x2; D(X); P(0,5 x < 2,5 ); F(x).
7. |
Xi |
1 |
2 |
x3 |
|
Pi |
0,2 |
0,4 |
P3 |
Известно, что М(Х) = 2,6. Найти: P3; x3; D(X); P(1,3 x ); F(x).
8. |
Xi |
x2 |
3 |
5 |
|
Pi |
P1 |
0,7 |
0,2 |
Известно, что М(Х) = 3,1. Найти: P1; x1; D(X); P( x < 2 ); F(x).
9. |
|
Xi |
|
2 |
|
4 |
|
5 |
|
|
|
Pi |
|
0,1 |
|
P2 |
|
0,7 |
|
|
Найти: |
P2; М(Х); D(X); P(1 x < 4 ); F(x). |
|||||||
10. |
|
Xi |
|
10 |
|
30 |
|
40 |
|
|
|
|
|
|
|||||
|
|
Pi |
|
P2 |
|
0,1 |
|
0,6 |
|
|
Найти: |
P1; М(Х); D(X); P( x < 2 ); F(x). |
|||||||
|
|
|
|
|
|
|
7 |
|
|
Задание 6
Обработайте статистические данные 100 независимых измерений некоторой физической величины Х.
а) Составьте статистическое распределение частот выборки Х.
б) Найдите эмпирическую функцию распределения и постройте ее график. в) Постройте полигон и гистограмму относительных частот.
г) Вычислите числовые характеристики:
выборочную среднюю;
выборочную дисперсию;
выборочное среднее квадратическое отклонение;
коэффициенты эксцесса и ассиметрии.
д) Выдвинув гипотезу о нормальном распределении, проверьте ее критерием согласия Пирсона при уровне значимости α = 0,05.
е) Найдите точечные и интервальные оценки параметров распределения (доверительную вероятность принять равной 0,95).
1.
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
172 |
63 |
173 |
64 |
178 |
73 |
165 |
68 |
165 |
67 |
164 |
60 |
172 |
73 |
170 |
65 |
162 |
55 |
169 |
62 |
164 |
53 |
164 |
60 |
156 |
55 |
177 |
72 |
176 |
65 |
161 |
60 |
169 |
63 |
170 |
66 |
171 |
66 |
167 |
60 |
172 |
66 |
167 |
58 |
171 |
65 |
162 |
65 |
172 |
64 |
166 |
63 |
169 |
62 |
174 |
68 |
171 |
62 |
163 |
65 |
170 |
65 |
171 |
63 |
162 |
56 |
164 |
59 |
169 |
66 |
181 |
68 |
167 |
71 |
167 |
65 |
173 |
77 |
168 |
65 |
165 |
57 |
165 |
67 |
169 |
71 |
170 |
65 |
156 |
53 |
172 |
67 |
170 |
61 |
171 |
62 |
170 |
61 |
164 |
57 |
181 |
68 |
175 |
67 |
166 |
57 |
166 |
67 |
174 |
73 |
167 |
55 |
173 |
66 |
159 |
57 |
157 |
53 |
163 |
58 |
179 |
80 |
176 |
72 |
175 |
59 |
170 |
61 |
167 |
63 |
172 |
65 |
172 |
60 |
159 |
55 |
169 |
62 |
165 |
63 |
160 |
57 |
160 |
62 |
168 |
50 |
168 |
61 |
173 |
77 |
161 |
57 |
173 |
66 |
173 |
77 |
166 |
55 |
161 |
55 |
185 |
82 |
171 |
63 |
165 |
55 |
164 |
70 |
163 |
63 |
177 |
78 |
161 |
51 |
156 |
54 |
175 |
66 |
166 |
57 |
163 |
65 |
159 |
48 |
167 |
61 |
167 |
59 |
164 |
57 |
168 |
66 |
163 |
64 |
164 |
60 |
180 |
76 |
167 |
65 |
8
2.
|
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
|
166 |
62 |
157 |
56 |
182 |
76 |
172 |
63 |
184 |
72 |
|
174 |
75 |
177 |
72 |
180 |
76 |
170 |
68 |
167 |
63 |
|
176 |
81 |
172 |
65 |
171 |
62 |
165 |
67 |
167 |
70 |
|
169 |
61 |
160 |
57 |
172 |
64 |
173 |
64 |
171 |
73 |
|
176 |
70 |
170 |
58 |
162 |
60 |
169 |
68 |
169 |
67 |
|
170 |
67 |
173 |
66 |
179 |
71 |
170 |
60 |
174 |
67 |
|
168 |
73 |
172 |
64 |
165 |
61 |
164 |
56 |
174 |
74 |
|
163 |
58 |
170 |
75 |
163 |
58 |
167 |
67 |
164 |
65 |
|
185 |
82 |
168 |
67 |
177 |
72 |
165 |
72 |
166 |
64 |
|
161 |
55 |
172 |
64 |
166 |
57 |
171 |
66 |
175 |
78 |
|
163 |
63 |
165 |
68 |
171 |
70 |
165 |
68 |
176 |
78 |
|
166 |
57 |
162 |
55 |
171 |
64 |
169 |
56 |
163 |
58 |
|
164 |
56 |
162 |
61 |
169 |
62 |
161 |
60 |
166 |
62 |
|
161 |
56 |
163 |
65 |
177 |
70 |
165 |
68 |
180 |
69 |
|
167 |
61 |
176 |
70 |
162 |
57 |
167 |
60 |
172 |
63 |
|
164 |
53 |
176 |
73 |
167 |
57 |
163 |
65 |
163 |
63 |
|
169 |
67 |
170 |
76 |
169 |
62 |
184 |
72 |
172 |
67 |
|
171 |
76 |
165 |
68 |
166 |
62 |
169 |
71 |
178 |
80 |
|
170 |
66 |
169 |
68 |
171 |
69 |
174 |
73 |
168 |
73 |
3. |
162 |
60 |
159 |
68 |
167 |
64 |
177 |
68 |
163 |
72 |
|
|
|
|
|
|
|
|
|
|
|
|
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
|
173 |
71 |
166 |
55 |
167 |
53 |
175 |
69 |
162 |
55 |
|
168 |
65 |
173 |
69 |
165 |
60 |
164 |
57 |
162 |
61 |
|
172 |
59 |
172 |
64 |
166 |
62 |
170 |
61 |
172 |
65 |
|
181 |
68 |
161 |
66 |
166 |
57 |
170 |
61 |
169 |
65 |
|
162 |
65 |
181 |
77 |
170 |
63 |
169 |
71 |
170 |
61 |
|
174 |
70 |
156 |
52 |
170 |
58 |
175 |
67 |
171 |
65 |
|
167 |
59 |
173 |
69 |
170 |
63 |
173 |
66 |
177 |
67 |
|
166 |
57 |
166 |
60 |
170 |
58 |
169 |
62 |
163 |
59 |
|
162 |
58 |
166 |
67 |
169 |
58 |
171 |
69 |
171 |
60 |
|
164 |
60 |
170 |
74 |
170 |
74 |
188 |
75 |
178 |
73 |
|
169 |
63 |
167 |
59 |
162 |
66 |
166 |
57 |
186 |
72 |
|
170 |
74 |
162 |
60 |
156 |
55 |
170 |
68 |
169 |
68 |
|
162 |
66 |
166 |
60 |
166 |
62 |
169 |
59 |
164 |
57 |
|
176 |
70 |
184 |
68 |
180 |
76 |
161 |
66 |
171 |
71 |
|
174 |
69 |
168 |
66 |
170 |
63 |
181 |
69 |
163 |
59 |
|
169 |
64 |
169 |
68 |
165 |
59 |
160 |
60 |
157 |
53 |
|
174 |
70 |
174 |
68 |
167 |
64 |
170 |
66 |
190 |
80 |
|
163 |
55 |
169 |
61 |
164 |
65 |
166 |
57 |
167 |
63 |
|
167 |
64 |
164 |
66 |
166 |
64 |
161 |
55 |
167 |
61 |
|
172 |
67 |
173 |
77 |
170 |
62 |
183 |
73 |
166 |
60 |
9
4.
|
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
|
168 |
68 |
179 |
63 |
169 |
73 |
165 |
66 |
168 |
68 |
|
166 |
57 |
181 |
69 |
156 |
53 |
176 |
73 |
172 |
72 |
|
170 |
65 |
172 |
70 |
169 |
70 |
161 |
62 |
180 |
75 |
|
171 |
67 |
171 |
64 |
164 |
59 |
172 |
67 |
173 |
77 |
|
168 |
70 |
161 |
59 |
169 |
57 |
157 |
69 |
161 |
58 |
|
184 |
72 |
180 |
76 |
178 |
71 |
164 |
60 |
161 |
59 |
|
169 |
71 |
170 |
63 |
159 |
54 |
167 |
61 |
171 |
59 |
|
169 |
71 |
179 |
69 |
163 |
64 |
166 |
60 |
176 |
67 |
|
169 |
71 |
171 |
69 |
182 |
76 |
173 |
72 |
177 |
70 |
|
177 |
72 |
173 |
64 |
174 |
75 |
177 |
72 |
169 |
62 |
|
164 |
70 |
172 |
64 |
164 |
66 |
160 |
62 |
167 |
65 |
|
168 |
62 |
162 |
54 |
167 |
64 |
165 |
57 |
168 |
68 |
|
163 |
64 |
166 |
63 |
169 |
64 |
163 |
68 |
170 |
63 |
|
164 |
70 |
176 |
81 |
169 |
65 |
178 |
66 |
181 |
68 |
|
166 |
55 |
168 |
68 |
180 |
73 |
171 |
65 |
162 |
52 |
|
171 |
65 |
172 |
72 |
164 |
66 |
173 |
68 |
169 |
68 |
|
174 |
79 |
167 |
59 |
168 |
58 |
178 |
60 |
164 |
60 |
|
176 |
65 |
161 |
55 |
188 |
75 |
171 |
65 |
170 |
63 |
|
176 |
67 |
171 |
69 |
166 |
57 |
164 |
60 |
165 |
69 |
|
158 |
56 |
165 |
61 |
178 |
62 |
167 |
64 |
161 |
55 |
5. |
|
|
|
|
|
|
|
|
|
|
|
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
|
162 |
52 |
163 |
57 |
154 |
52 |
165 |
60 |
178 |
66 |
|
169 |
68 |
155 |
61 |
160 |
62 |
162 |
58 |
180 |
65 |
|
168 |
63 |
182 |
75 |
161 |
59 |
164 |
60 |
165 |
69 |
|
187 |
63 |
161 |
51 |
180 |
76 |
178 |
80 |
176 |
70 |
|
169 |
58 |
168 |
67 |
171 |
62 |
164 |
59 |
164 |
56 |
|
170 |
74 |
164 |
62 |
175 |
67 |
164 |
60 |
169 |
61 |
|
160 |
62 |
171 |
66 |
173 |
66 |
164 |
62 |
161 |
57 |
|
171 |
60 |
164 |
62 |
161 |
56 |
171 |
76 |
163 |
54 |
|
174 |
70 |
167 |
62 |
182 |
76 |
169 |
66 |
171 |
70 |
|
170 |
63 |
180 |
69 |
174 |
75 |
173 |
63 |
162 |
65 |
|
173 |
66 |
167 |
63 |
169 |
56 |
163 |
58 |
174 |
73 |
|
171 |
64 |
170 |
61 |
175 |
67 |
174 |
70 |
167 |
59 |
|
161 |
59 |
172 |
72 |
171 |
60 |
172 |
72 |
166 |
57 |
|
163 |
54 |
171 |
73 |
167 |
53 |
169 |
64 |
168 |
54 |
|
176 |
78 |
169 |
58 |
171 |
63 |
178 |
71 |
174 |
66 |
|
171 |
73 |
170 |
74 |
168 |
58 |
162 |
65 |
171 |
73 |
|
169 |
67 |
190 |
80 |
167 |
55 |
169 |
62 |
172 |
67 |
|
173 |
68 |
156 |
55 |
176 |
67 |
168 |
61 |
163 |
65 |
|
174 |
65 |
168 |
59 |
163 |
63 |
165 |
56 |
170 |
62 |
|
165 |
61 |
176 |
75 |
178 |
69 |
172 |
70 |
163 |
54 |
10
