Символическое выражение категорических суждений

Указанные виды суждений принято обозначать гласными буквами латинских слов affirmo(утверждаю) иnego(отрицаю). Первые гласные буквы этих слов обозначают общие суждения, а вторые – частные.

Общеутвердительные суждения обозначаются буквой А.

Общеотрицательные – Е.

Частноутвердительные – I.

Частноотрицательные – О.

Современная символическая логика вводит специальные средства для обозначения А, Е, I, О: кванторы, логические переменные и логические постоянные.

А - – “Все S суть P” (для всякого х верно, что если он обладает свойством S, то обладает свойством P).

I – – “Некоторые S суть P” (существуют х, обладающие свойством S и свойством P).

E – – “Ни одно S не суть P” (для всякого х верно, что если он обладает свойством S, то не обладает свойством P).

O – – “Некоторые S не суть P” (существуют х, обладающие свойством S и не обладающие свойством P).

§3. Распределенность терминов в суждении

Распределенность терминов– это количественная характеристика субъекта и предиката в суждении.

Термин считается распределенным, если его объем либо полностью включен в объем другого термина, либо полностью из него исключен. Или иначе, термин считается распределенным, если он мыслится в полном объеме. Для распределенного термина характерно кванторное слово «все», для нераспределенного – «некоторые».

Графически распределенность терминов изображается с помощью круговых схем и штриховки той части терминов, которые мыслятся в суждении.

Вобщеутвердительном суждении «ВсеSсутьP», субъект распределен, так как мыслится в полном объеме, предикат не распределен, т.к. его объем не исчерпывается лишь объемом субъекта. Например, «Карась- рыба».

Исключение составляют выделяющие суждения, в которых объем субъекта и предиката совпадают. Например, «Все люди суть разумные существа», «Александр Сергеевич Пушкин – автор романа «Евгений Онегин»».

В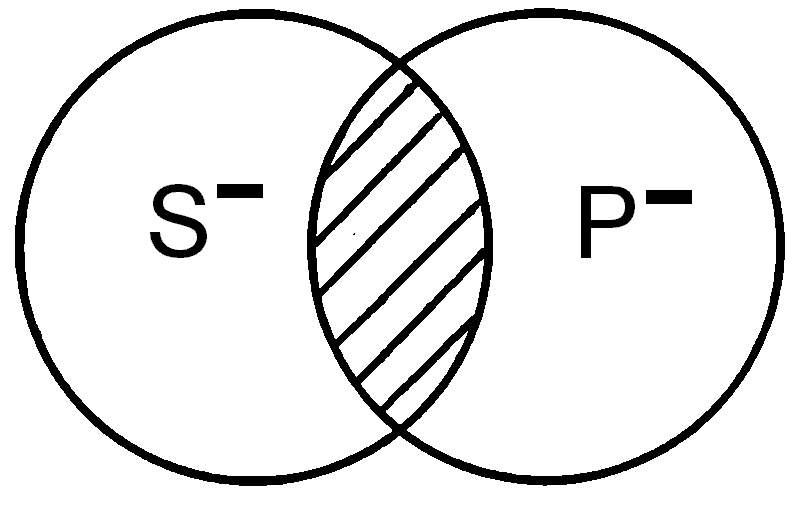частноутвердительном суждении «НекоторыеSсуть Р» ни субъект, ни предикат не распределены, т.к. мыслятся не в полном объеме. Например, «Некоторые юристы являются депутатами Государственной Думы».

Исключение составляют частновыделяющие суждения, в которых предикат мыслится в полном объеме, следовательно распределен. Например, «Некоторые прямоугольники являются квадратами».

Вобщеотрицательном суждении «Ни одноSне суть Р» и субъект, и предикат являются распределенными, т.к. их объемы полностью исключают друг друга. Например, «Ни один крокодил не летает».

Вчастноотрицательном суждении («НекоторыеSне суть Р») субъект не распределен, т.к. мыслится лишь в некоторой части, предикат распределен, т.к. его объем полностью исключен из объема субъекта. Например, «Некоторые студенты не являются спортсменами».

Общая схема распределенности терминов в суждении такова: субъекты распределены в общих суждениях, предикаты – в отрицательных.

	S	P
A	+	-
E	+	+
I	-	-
O	-	+

Отрицание суждения

Отрицаниемназывается логическая операция, посредством которой образуется новое суждение, принимающее логическое значение истины тогда и только тогда, когда исходное суждение ложно и, наоборот, логическое значение ложности тогда, когда исходное суждение истинно. Отрицание отрицания (двойное отрицание) есть возврат к исходному логическому значению. Логическое значение отрицания и двойного отрицания можно представить в виде матрицы, которая называется таблицей истинности.

И	Л	И
Л	И	Л