Алгебра(матрицы)

1Комплексные числа

1.1Определение; операции с комплексными числами

Определение 1. Комплексное число это пара вещественных чисел (a; b), операции сравнения и арифметические вводятся согласно аксиомам:

1. (a; b) = (c; d) тогда и только тогда, когда a = c и b = d.

2.(a; b) + (c; d) = (a + c; b + d).

3.(a; b)(c; d) = (ac bd; ad + bc).

4.Пара (a; 0) отождествляется с вещественным числом a. Обычно используют запись a + bi.

В записи a + bi символ i называется мнимой единицей; операции

с комплексными числами аналогичны операциям с действительными числами, только надо помнить, что i2 = 1. Заметим, что при возведении

вещественного числа в квадрат получается положительное число, поэтому i не может быть обычным вещественным числом.

Предложение 1. Для комплексных чисел выполняются следующие свойства операций:

1.Коммутативность сложения: (a + ib) + (c + id) = (a + c) + i(b + d) = (c + id) + (a + ib).

2.Ассоциативность сложения: ((a + ib) + (c + id)) + (f + ih) = (a + ib) + ((c + id) + (f + ih))

3.(a + ib) + (0 + i0) = a + ib, так что число (0 + i0) = 0 играет роль нуля и в комплексных числах.

4.Коммутативность умножения: (a + ib)(c + id) = (c + id)(a + ib).

5.Дистрибутивность: ((a + ib) + (c + id))(f + ih) = (a + ib)(f + ih) + (c + id)(f + ih).

6.Ассоциативность умножения: ((a; b)(c; d))(f; h) = (a; b)((c; d)(f; h)).

7.(a + ib)(1 + i0) = (a + ib), то есть число (1 + i0) = 1 играет роль единицы в комплексных числах.

8.(a + bi)0 = 0.

9.z1z2 = 0 , z1 = 0 èëè z2 = 0.

Определение 2. Комплексное число a bi будем называть сопряженным к числу a + bi, и обозначать это следующим образом: a + bi = a bi.

1

Предложение 2 (Свойства сопряжения). 1. Сумма и произведение сопряженных чисел число вещественное.

2.z1 + z2 = z1 + z2

3.z1z2 = z1 z2

4.z2 z2

5.z1n = z1nz1 z1=

Доказательство на практике или самостоятельно.

1.Для любого комплексного числа (a + ib) 6= 0 существует обратное число, то есть (a + ib) 1 такое, что (a; b)(a; b) 1 = (a; b) 1(a; b) = 1.

2.Обратное число единственно.

3.Из предыдущего пункта следует, что комплексные числа можно

Внимание! вещественная и мнимая часть комплексного числа всегда вещественны!

1.2Тригонометрическая форма записи комплексного числа; формула Муавра; корни из комплексных чисел.

Согласно определению, комплексное число определяется парой вещественных чисел (a; b). Такую пару естественно изображать в

виде точки плоскости с координатами (a; b). Таким образом, комплексное

число можно представить в виде точки плоскости, или вектором из начала координат в эту точку. Тогда операция сложения комплексных чисел естественно интерпретируется как сложение векторов. А вычитание комплексных чисел эквивалентно вычитанию соответствующих векторов.

Рассмотрим на плоскости полярную систему координат, тогда каждой точке (комплексному числу) может быть сопоставлена пара чисел (r; ).

Число r = jzj называется модулем комплексного числа z, а угол = Argz, называется аргументом z, аргумент числа определяется не однозначно. А именно с точностью до 2 k, где k произвольное целое число.

2

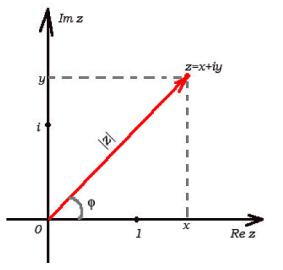
Из связи полярных и прямоугольных координат очевидно следует, что если z = x + yi, то

Таким образом, комплексное число z = a + bi можно представить в виде:

z = r(cos + i sin )

такое представление называется тригонометрической формой записи числа z.

Предложение 3. Комплексные числа равны тогда и только тогда, когда равны их модули и аргументы отличаются на 2 k, где k произвольное

целое число.

Предложение 4. Пусть есть два комплексных числа z1; z2 представленных в тригонометрической форме. Тогда

То есть при умножении, модули перемножаются, а аргументы складываются. При делении, модули делятся, а аргументы вычитаются.

Поскольку в тригонометрической форме легко перемножать комплексные числа, легко и возводить их в степени.

3

zn = rn(cos n + i sin n )

Эта формула называется формулой Муавра.

Для натуральных чисел n формула Муавра легко следует из первого пункта предложения; для n = 0 формула очевидна. Для n < 0 формулу легко доказать, принимая во внимание 1 = 1 + 0i = 1(cos 0 + i sin 0).

Пример. Вычислим число (1 + i)53. С помощью бинома Ньютона это

Определение 4. Число w называется корнем n-ой степени из комплексного числа z, если wn = z.

Поэтому у нас не бесконечное количество корней, а всего n корней: w =

1.3Корни из единицы

Отдельно мы рассмотрим корни n-той степени из 1. Так как j1j = 1 и arg(1) = 0, то корни n-той степени из 1, обозначаемые как

Корни из единицы очень хорошо изображаются на плоскости, они представляют собой правильный n-угольник, вписанный в единичную

окружность с одной из вершин в 1.

Определение 5. Корень n-той степени из 1, " называется первообразным корнем степени n, если "m 6= 1 ïðè âñåõ 0 < m < n.

Теорема 1. Число "k является первообразным корнем из 1, степени n тогда и только тогда, когда k и n взаимно просты.

Proof. Действительно, "nk = 1 для любых k. Пусть k и m взаимно просты, и пусть "k не первообразный корень. Тогда существует 0 < m < n такое, что "mk = 1, то есть = 2l , что равносильно тому, что km нацело делится

4

на n, то так как k и n взаимно просты, то m делится на n, что невозможно так как 0 < m < n.

Теперь обратно, то есть "k первообразный степени n, покажем, что k и n взаимно просты. Пусть это не так, и пусть d 6= 1 общий делитель

k = k1d è n = n1d, тогда "nk1 , рассмотрим аргумент этого числа, он равенn1 = 2k1 , òî åñòü "nk1 = 1 è ïðè ýòîì n1 < n, что противоречит

первообразности корня "k. Таким образом k и n взаимно просты.

Предложение 5 (Свойства корней из 1). 1. Произведение двух корней степени n из 1, также является корнем степени n из 1.

2.Число, обратное корню степени n из 1, также корень степени n из 1.

3.Если z корень из 1, то z 1 = z.

4.Пусть " первообразный корень степени n из 1, тогда любой другой корень этой степени получается возведением " в некоторую степень.

Proof. Доказать 1 и 2.

Доказательство 3. Действительно "k корень степени n из 1. Пусть "k = "l, тогда "k l = 1, то есть, так как корень первообразный, то k = l или k l = nm. То есть "k, где k = 0; 1; 2; : : : ; n 1 это все разные числа, и они корни из 1, то есть это все корни из 1.

2 Вывод тригонометрических формул с помощью комплексных чисел

Пример. Предположим, нам надо вычислить cos 3 . Рассмотрим комплексное число " = cos + i sin . Заметим, что "3 = cos 3 + i sin 3

по формуле Муавра. Поскольку действительные части слева и справа совпадают, можно записать равенство

Re("3) = cos 3

Для того, чтобы найти Re("3) возведем в куб выражение cos + i sin и возьмем только те слагаемые, которые без i. Получим: cos3 3 cos sin2 .

Окончательно: cos 3 = cos3 3 cos sin2 .

Пример. Вычислить сумму 1 + cos + cos 2 + : : : + cos n . Рассмотрим число " = cos + i sin . Заметим, что искомая сумма равна

действительной части комплексного числа 1 + " + "2 + : : : + "n

Но эта новая сумма геометрическая прогрессиия, которую мы можем легко просуммировать. " + "2 + : : : + "n = "n 1

" 1 .

5

6

3Матрицы и определители

3.1Матрицы. Определение. Матричные операции

Определение 6. Прямоугольная таблица, в которой n строк и m

Можно использовать запись A = (aij)n m (которая означает, что за элементами матрицы A мы закрепили обозначение aij), а размеры матрицы A n строк и m столбцов.

Примечание. В качестве множества K будем рассматривать множества R (действительных чисел), C (комплексных чисел), Z (целых чисел) и т.д.

Позже будем брать и другие множества, которые мы пока не изучили. Введем операции на множестве матриц.

Определение 7 (Матричные операции).

1.Две матрицы называются равными, если у них одинаковые размеры и равные элементы на одинаковых местах.

2.Чтобы умножить матрицу на число из множества K надо просто все ее элементы умножить на это число.

3.Сложить можно две матрицы одного размера, для этого надо просто сложить одноименные элементы матриц. (Аналогично можно вычитать матрицы).

4.Умножение матриц. Можно умножить 2 матрицы, если количество столбцов первой матрицы равно количеству строк второй матрицы. При этом в результирующей матрице количество строк как в первой, а количество столбцов как во второй

Cn m = An kBk m; а ее элементы получаются по формуле cij =

k

P

aitbtj.

t=0

Пример умножения двух матриц.

Свойства операций:

7

1.A + B = B + A (коммутативность сложения);

2.(A + B) + C = A + (B + C) (ассоциативность сложения);

3.A(B + C) = AB + AC; (B + C)A = BA + CA (дистрибутивность);

4.A(BC) = (AB)C (ассоциативность умножения);

5.коммутативности умножения нет!

Пример некоммутативности: 1) пример выше не пройдет по размерам.

0 0

è0 1 .

Доказательство: 1, 2, 3 элементарно.

4. Доказательство. Сначала проверяем размеры. An k, Bm x, Cy z. Для того, чтобы было возможно умножение (AB)C надо, чтобы k = m и x = y. Результат получается размера n z. Для того, чтобы было возможно умножение A(BC) необходимо, чтобы x = y и m = k. Результат получается размера n z. Пока что все хорошо: если возможно расставить скобки

одним образом, то возможно их расставить и другим образом; кроме того, результат получается одного размера.

Обозначим D = AB; F = BC и Q = DC; R = AF . Мы уже знаем, что размеры матриц Q и R одинаковы. Осталось доказать, что они состоят из одинаковых элементов. Вычислим qij è rij.

qij = di1c1j + di2c2j + ::: + dixcxj =

Расписываем все элементы dit исходя из того, что D = AB:

= (ai1b11 + ai2b21 + : : : + aimbm1)c1j+ +(ai1b12 + ai2b22 + : : : + aimbm2)c2j+ + : : : +

+(ai1b1x + ai2b2x + : : : + aimbmx)cxj =

раскрываем скобки и группируем все эти элементы по-другому. Заметим, что в первом столбике всегда встречается ai1, во втором ai2 è т.д. Вынесем из каждого столбика эту ait за скобку. Получим:

= ai1(b11c1j + b12c2j + : : : + b1xcxj)+ +ai2(b21c1j + b22c2j + : : : + b2xcxj)+ + : : : +

+aim(bm1c1j + bm2c2j + : : : + bmxcxj) =

Рассмотрим внимательно, что за суммы стоят в скобках. bt1c1j + bt2c2j + : : : + btxcxj = ftj Получаем

= ai1f1j + ai2f2j + ::: + aimfmj = rij.

Вот мы и доказали, что R = Q, т.е. (AB)C = A(BC).

Заметим, что есть некоторые особые матрицы: например, нулевая (все элементы которой нули; бывает любого размера) и единичная (по главной диагонали идут единицы, все остальные элементы нули; бывает только квадратная). Главная диагональ матрицы это элементы a11; a22; : : : ; ann.

8

Нулевая матрица при сложении не изменяет матрицу; зануляет любую матрицу при умножении (с любой стороны). Единичная не меняет матрицу при умножении (с любой стороны).

Бывает так, что при умножении двух матриц получается нулевая, даже если ни одна из исходных матриц не была нулевой.

Пример.

Определение 8. Матрица B называется обратной к матрице A если AB = BA = E. Обозначение: A 1.

Заметим, что обратные матрицы могут быть только у квадратных матриц. Но никто не гарантирует, что у любой квадратной матрицы есть обратная!

иначе в нашем предыдущем примере AB = O мы умножили бы равенство на матрицу A 1 слева и получили бы A 1(AB) = (A 1A)B = EB = B, а с другой стороны A 1O = O. Ò.å. B = O, ÷òî íå òàê.

Предложение 6. Åñëè AB = E, CA = E, òî B = C.

В частности, из этого следует, что если обратная матрица существует, она единственная.

Действительно, умножим равенство CA = E на матрицу B справа. Получим (CA)B = C(AB) = CE = C, а с другой стороны EB = B. Поэтому C = B.

Определение 9. Рассмотрим матрицу AT = (aji). Матрица AT называется транспонированной к матрице А.

При транспонировании строки матрицы A становятся столбцами матрицы AT , а столбцы матрицы A становятся строками матрицы AT . Èõ

порядок при этом не изменяется.

Свойства транспонирования и обращения:

1.(A + B)T = AT + BT .

2.(A 1) 1 = A

3.(AT )T = A

4.(AB) 1 = B 1A 1

5.(AB)T = BT AT

6.(A 1)T = (AT ) 1

9

1, 2, 3 элементарно.

4. (AB)(B 1A 1) = A(B(B 1A 1)) = A((B 1)A 1) = A(EA 1) = E.

Перемножим в обратном порядке, проведем аналогичные рассуждения, получим (B 1A 1)(AB) = E. Таким образом матрица (B 1A 1)

обратная к AB, что и требовалось.

5. Пусть An m. Тогда чтобы можно было умножить AB у матрицы B

размеры m k. Поэтому BT ; AT

k m m n. Если можно произвести умножение справа, можно произвести умножение и слева и наоборот. У матрицы C =

AB размеры n k у матрицы D = BT AT размеры k n. Т.е. размеры

t=1

умножения матриц числа, которые стоят на нужных местах в матрицах BT è AT ).

Получаем cij = dji, что и требовалось доказать.

6.(AT )(A 1)T = по свойству 4 (A 1A)T = ET = E.

3.2Определитель

Очень важной характеристикой квадратных матриц является определитель.

Определение 10. Определителем квадратной матрицы A = (aij) размерами n n называется число, полученное по следующим правилам:

Если n = 1, то определителем матрицы (a11) является единственное число этой матрицы.

Пусть мы уже умеем вычислять определители порядка n = k 1; тогда определитель порядка n = k вычисляется по формуле:

k

X

jAj = a11M11 a12M12 + ::: + ( 1)k+1a1kM1k = ( 1)1+ja1jM1j; j=1

ãäå M1j определитель порядка n 1, полученный из матрицы А вычеркиванием первой строки и j-ого столбца.

Обозначение jAj или detA.

Доказать формулу определителя 2х2 ("крестик") и 3х3 ("звездочка"). Действительно, мы уже из определения определителя знаем, как

вычислять определитель 1 1. Тогда для вычисления определителя 2 2

10