Лабораторная работа № 3 изучение законов соударения тел

Цель работы: исследование удара, изучение законов сохранения импульса и механической энергии при ударе, определение силы взаимодействия между шарами

Основные теоретические сведения

Удар – совокупность явлений, возникающих при кратковременном приложении к телу внешних сил, например, при взаимодействии с другим движущимся относительно него телом, связанных со значительным изменением его скорости за очень короткий промежуток времени.

Абсолютно неупругим называют такой удар, после которого скорости обоих соударяющихся тел оказываются одинаковыми.

Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает – кинетическая энергия тел полностью или частично превращается во внутреннюю энергию. При абсолютно неупругом ударе выполняется лишь закон сохранения импульса и имеет место закон сохранения суммарной энергии различных видов – механической и внутренней.

Абсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие немеханические виды энергии. Потенциальная энергия упругой деформации вновь переходит в кинетическую энергию, и тела разлетаются со скоростями, величина которых определяется двумя условиями – сохранением полной энергии и сохранением полного импульса системы тел.

Рассмотрим центральный абсолютно упругий удар двух шаров. Удар называется центральным, если шары до удара движутся вдоль прямой, проходящей через их центры.

Пусть шары массой и движутся до соударения со скоростями и , а после соударения со скоростями и . На основании закона сохранения импульса можно записать:

. (3.1)

На основании закона сохранения энергии имеем:

. (3.2)

Перепишем эти равенства в виде:

, (3.3)

. (3.4)

Поделив (3.4) на (3.3), получим:

(3.5)

или

. (3.6)

Таким образом, при абсолютно упругом ударе относительная скорость шаров остается неизменной величиной.

Умножая уравнение (3.5) на , а затем на и вычитая его из уравнения (3.3), получим:

, (3.7)

. (3.8)

Рассмотрим два частных случая.

1. Сумма импульсов обоих шаров до ударов равна нулю, то есть

. (3.9)

Тогда

, ,

отсюда, применяя (3.9), находим: ,, то есть скорости обоих шаров при ударе только изменяют свой знак.

2. Один шар до удара покоится: .

Тогда , .

После удара второй шар двинется в ту же сторону, куда двигался первый до удара. Скорость и поведение первого шара зависит от соотношения масс.

а) Если , то первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью. Скорость второго шара после удара больше, чем скорость первого до удара.

б) Если , то направление движения первого шара при ударе изменяется – шар отскакивает обратно. Второй шар движется в ту сторону, в которую двигался первый до удара, но с меньшей скоростью.

в) Массы шаров одинаковы:. Тогда,, то есть шары при ударе обмениваются скоростями.

В случае абсолютно неупругого удара

, (3.10)

где – одинаковая для обоих шаров скорость после удара.

Из (3.10) следует, что

. (3.11)

В частном случае, когда массы шаров равны, .

В случае не абсолютно упругого удара часть кинетической энергии шаров при соударении переходит в энергию остаточной деформации. Тогда . Отсюда можно получить, что, то есть при неупругом ударе относительная скорость их меняет свое направление на противоположное, уменьшаясь в то же время по абсолютной величине.

Неупругий удар сопровождается остаточной деформацией. Если пре­не­бречь всякого рода сопротивлениями, закон сохранения энергии для удара двух одинаковых шаров запишется так:

, (3.12)

где – энергия остаточной деформации одного шара, относящаяся к одному соударению.

Задания данной работы предусматривают про­верку выражений закона сохранения импульса при упругом и абсолютно неупругом ударах.

Экспериментальная установка и методика измерений

Схема лабораторной установки показана на рис.3.1. К штативу 1 прикреплены два шара. Углы отклонения подвесов от вертикали определяются по шкалам 3. Электромагнит 4 служит для удержания одного из шаров в отклоненном положении.

Отведем один из шаров (например, правый) на некоторый угол и отпустим без начальной скорости. Отклоненный шар будет двигаться вниз, разгоняясь, при этом его потенциальная энергия будет переходить в кинетическую. Пусть столкновение со вторым шаром происходит в тот момент, когда нить первого шара становится вертикально. По закону сохранения механической энергии (см. рис. 3.2)

, (3.13)

где – масса шара,– ускорение свободного падения,– высота шара в отведенном положении относительно нижней точки траектории,– скорость первого шара в нижней точке перед соударением со вторым.

Из рис. 3.2 видно, что

, (3.14)

где – расстояние от точки подвеса до центра тяжести шара, – угол начального отклонения нити.

Подставляя (3.13) в (3.14) и преобразуя уравнение, найдем выражение для скорости через угол начального отклонения:

, (3.15)

Массы шаров подобраны так, чтобы после удара они разлетелись в разные стороны. После удара шары получают скорости и(рис. 3. 3), и, разлетаясь, отклоняют нити на максимальные углыи, соответственно.

Аналогично соотношению (3.15) получаем:

, . (3.16)

Если удар происходит достаточно быстро так, что нити во время удара не успевают отклониться на заметный угол, то в направлении горизонтальной оси оx не возникает внешних сил и выполняется закон сохранения импульса в проекции на эту ось:

. (3.17)

Коэффициент восстановления скорости определяется как отношение относительной скорости шаров после удара к относительной скорости шаров до удара:

. (3.18)

В данном случае формула (3.18) с учетом (3.15) и (3.16) преобразуется к виду

(3.19)

Для абсолютно упругого удара = 1. В случае столкновения реальных шаров, столкновение не является абсолютно упругим, и< 1.

Кроме коэффициента восстановления скорости соударение тел характеризуется коэффициентом восстановления энергии, равным отношению кинетической энергии тел после удара к их кинетической энергии до удара:

. (3.20)

Учитывая, что скорость второго шара до удара = 0 и подставляя для скоростей выражения (3.15) и (3.16), находим рабочую формулу для коэффициента восстановления энергии:

. (3.21)

Если известна длительность удара , то из второго закона Ньютона по изменению импульса одного из шаров (например, левого) можно определить среднюю силу взаимодействия между шарами:

или. (3.22)

Работа выполняется в такой последовательности.

1. Подключить электромагнит 4 с помощью разъёма 5 и клеммы верхнего кронштейна 7 к электронному блоку 8.

2. Вставить шары 2 в скобы подвеса. С помощью регулировочных опор выставить основание установки таким образом, чтобы нижние визиры скоб подвеса указывали на нули шкал.

3. Отрегулировать положение шаров в вертикальной и горизонтальной плоскостях до совмещения верхних визиров скоб подвеса. Регулировка производится с помощью изменения длины подвеса шаров, а также изменения положения узлов крепления нитей на верхнем кронштейне.

4. На пульте блока нажать кнопку «СБРОС». При этом на табло индикации высветятся нули, на электромагнит будет подано напряжение.

5. Отвести правый шар и зафиксировать его с помощью электромагнита. Определить начальный угол отклонения первого шара .

6. Нажать кнопку «ПУСК», при этом произойдет удар шаров. По таймеру блока определить время соударения шаров .

7. Определить время соударения для различных пар шаров по методике, описанной в п. 4 ÷ 6.

8. В правую скобу подвеса вставить алюминиевый шар со стальной вставкой, а в левую – латунный или стальной шар.

9. Выполнить п. 4 ÷ 6. При помощи шкал визуально определить углы отскока не менее трех раз. Найти среднее значение каждого из углов и.

Обработка результатов экспериментов

1. По формуле (3.15) определить скорость первого шара перед ударом. Используя средние значения углов отскока, по формулам (3.16) определить скорости обоих шаров сразу после удараи. Проверить выполнение закона сохранения импульса (3.17).

2. Используя средние значения углов отскока по формулам (3.19) и (3.21) определить коэффициенты восстановления скорости и энергии.

3. Используя найденное выше значение по формуле (3.22) определить среднюю силу, с которой шары действуют друг на друга во время удара.

Расчет погрешностей

1. По методике расчета случайных погрешностей прямых измерений Приложения 2 найти погрешности измерения углов отклонения и. Для этого по формуле (П2.1) определить средние значения углов отклонения и .Затем по формулам (П2.2), (П2.3), где X_i = _i, =найти среднеквадратическое отклонение и абсолютную величину погрешности.

2. Найти погрешность определения ипо методике вычисления погрешностей косвенных измерений:

; . (3.23)

3. Найти погрешность определения средней силы удара по формуле:

. (3.24)

Лабораторная работа № 4

ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ С ПОМОЩЬЮ МАЯТНИКА МАКСВЕЛЛА

Цель работы:изучение сложного движения твердого тела и закона сохранения энергии в таком движении, определение момента инерции маятника Максвелла

Основные теоретические сведения

Рассмотрим плоское движение твердого тела, при котором все точки твердого тела перемещаются в параллельных плоскостях. Примером такого движения может служить качение цилиндра по плоскости. Плоское движение может быть представлено как суперпозиция двух движений – поступательного и вращательного.

Движение центра масс твердого тела определяется уравнением:

, (4.1)

где – скорость центра масс,– сумма всех внешних сил, действующих на тело.

Чтобы полностью определить движение тела, надо, кроме того, написать уравнение моментов относительно какой-либо произвольно выбранной неподвижной оси. Однако положение движущегося тела относительно неподвижной оси будет все время изменяться и связь между моментом импульса и угловой скоростью будет сложной. Для случая плоского движения задача существенно упрощается, так как можно записать уравнение моментов относительно оси, жестко связанной с телом и проходящей через его центр масс. Поскольку эта ось неподвижна относительно тела, можно записать основное уравнение динамики вращательного движения:

, (4.2)

где – момент внешних сил относительно той же оси,– момент инерции относительно той же оси.

Таким образом, уравнение (4.1) определяет скорость поступательного движения тела, а уравнение (4.2) – угловую скорость вращательного движения.

Применим полученные уравнения к движению маятника Максвелла, общий вид которого изображен на рис.4.1. Маятник Максвелла представляет собой металлический диск 1, в середине которого укреплен стержень2, а к ободу крепится съемное кольцо3. К концам стержня прикреплены две капроновые нити4. Они наматываются на стержень от концов его к диску. При освобождении маятника он начинает движение: поступательное вниз и вращательное вокруг своей оси симметрии. Вращение, продолжаясь по инерции в низшей точке движения, когда нити уже размотаны, приводит вновь к наматыванию нитей на стержень, а следовательно, и к подъему маятника.

Уравнения движения маятника без учета сил трения имеют вид:

, (4.3)

, (4.4)

, (4.5)

где т – масса маятника, I – момент инерции маятника, g – ускорение силы тяжести, r – радиус стержня, T – натяжение нити, а – ускорение поступательного движения центра масс маятника,  – угловое ускорение маятника.

Ускорение а может быть получено по измеренному времени движения t и проходимому маятником расстоянию h из уравнения

. (4.6)

Уравнения (4.3), (4.4), (4.5) дают:

, (4.7)

. (4.8)

Пользуясь этими уравнениями с учетом (4.6), можно определить момент инерции маятника Максвелла по экспериментально полученным данным:

. (4.9)

Расстояние h, проходимое маятником, измеряется по вертикальной рейке с делениями.

Момент инерции маятника можно рассчитать теоретически.

Момент инерции маятника Iявляется аддитивной величиной:

, (4.10)

где ,,– соответственно моменты инерции оси, диска и кольца маятника.

Момент инерции оси маятника массойравен

. (4.11)

Момент инерции диска массойможет быть найден по формуле:

, (4.12)

где – радиус диска.

Момент инерции кольца массойнаходится по формуле

, (4.13)

где – средний радиус кольца,b – ширина кольца.

Полная кинетическая энергия маятника складывается из энергии поступательного перемещения центра масс, совпадающего с центром оси, и из вращения маятника вокруг оси:

. (4.14)

Зная линейное и угловое ускорения, можно найти скорость движения оси маятника и угловую скорость его вращения:

. (4.15)

Экспериментальная установка

и методика измерений

1. Надеть одно из колец 3 на диск маятника.

2. Установить нижний кронштейн с фотодатчиком 5 в крайнее нижнее положение шкалы так, чтобы верхняя плоскость кронштейна совпала с одной из рисок шкалы.^

3. Произвести регулировку положения основания установки при помощи регулировочных опор так, чтобы диск на бифилярном подвесе находился в центре окна фотодатчика.

4. Установить необходимую длину бифилярного подвеса таким образом, чтобы нижний край диска маятника находился на 4…5 мм ниже оптической оси фотодатчика, при этом ось датчика должна занять горизонтальное положение. По шкале стойки определить ход маятника h.

5. Подключить фотодатчик 5 и электромагнит 6 к электронному блоку 7. Нажать кнопку «Сеть». При этом должно включиться табло индикации.

6. Аккуратно вращая маятник, зафиксировать его в верхнем положении при помощи электромагнита 6, при этом необходимо следить за тем, чтобы нить наматывалась на ось виток к витку. В зафиксированном положении нити подвеса должны быть прослаблены.

7. Нажать на кнопку «Сброс», чтобы убедиться, что на индикаторах устанавливаются нули.

8. Нажать на кнопку «Пуск» блока 7. Происходит растормаживание электромагнита, маятник начинает опускаться, и таймер блока начинает отсчет времени. При пересечении маятником оптической оси фотодатчика отсчет времени прекратится. Записать показания таймера, то есть время движения t.

9. Для повышения точности измерения п. 6 – 8 повторить 5 ÷ 6 раз.

10. С помощью штангенциркуля измерить радиусы оси маятника, диска и кольца, а также ширину кольца

11. Повторить измерения для других колец.

Обработка результатов экспериментов

1. Вычислить среднее значение времени прохождения маятником путиh при N числе измерений.

2. Вычислить по методике расчета погрешности прямых измерений, задавая доверительную вероятностьр₀ и коэффициент Стьюдента по таблице П2.1 Приложения 2, при этом,.

3. По формуле (4.9), в которой, вычислить среднее значение момента инерции.

4. По формулам (4.11) – (4.14) вычислить теоретическое значение момента инерции маятника I. Сравнить два полученных значения момента инерции и отметить в отчете, совпадают ли они в пределах точности эксперимента, указать возможные причины несовпадения.

5. По формулам (4.15) рассчитать линейную и угловую скорости маятника в нижней точке движения.

6. По формуле (4.14) найти кинетическую энергию маятника в этот момент, сравнить ее с начальной потенциальной энергией . По разности этих энергий оценить работу сил сопротивления.

Расчёт погрешностей

1. По формуле

(4.16)

вычислить случайную погрешность измерения величины ΔI_сл.

2. По формуле

(4.17)

вычислить приборную погрешность измерения величины ΔI_п .

3. Суммарную погрешность величины I рассчитать по формуле:

. (4.18)

4. Результат представить в виде:.

Лабораторная работа № 5

ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА МЕТОДОМ ИЗГИБА

Цель работы:изучение упругих деформаций различных материалов.

Основные теоретические сведения

Рассмотрим деформацию тонкой пластины под действием усилия F. Если материал пластины однороден, то все одинаковые участки ее в любом месте будут растянуты одинаково. Такая деформация называется одномерной. Пластина будет иметь одинаковую деформацию растяжения, характеризуемую относительным удлинением:

, (5.1)

где – удлинение какого-либо участка пластины, имевшей первоначально длинуl.

Для любых отрезков, и в том числе для всей пластины, величина одинакова и зависит от величины растягивающей силыF.

Под действием этой силы в пластине возникнут внутренние усилия, с которыми действуют друг на друга частицы материала пластины. Величина усилия, действующая на единицу площади поперечного сечения S, называется напряжениемσ:

. (5.2)

Из эксперимента известно, что при небольших усилиях напряжение и деформацияпримерно пропорциональны друг другу:

. (5.3)

Эта зависимость носит название закона Гука, а коэффициент пропорциональности Е называется модулем Юнга и является одной из существенных характеристик данного материала. Модуль Юнга считается положительным, так что знак напряжения совпадает со знаком деформации. Область напряжений и деформаций, в которой действует закон Гука, называется областью пропорциональности. Средние величины модуля Юнга для ряда материалов даны в табл. 1 Приложения 1.

Примером двумерного деформируемого твердого тела является изгиб пластины под действием сил, приложенных нормально к ее оси – поперечных нагрузок.

Если прямую упругую пластину обоими концами свободно положить на твердые опоры и нагрузить в середине силой Р, то середина пластины опустится, то есть она согнется (рис. 5.1). При таком изгибе верхние слои пластины будут сжиматься, а нижние – растягиваться. Некоторый средний слой, который называется нейтральным, сохранит длину и только претерпит искривление.

Перемещение d, которое получает середина пластины, называется стрелой прогиба. Стрела прогиба тем больше, чем больше нагрузка, кроме того, она зависит от формы и размеров пластины и от ее модуля упругости.

Найдем связь между стрелой прогиба и характеристиками упругой пластины. Рассмотрим пластину прямоугольного сечения длиной l, толщиной h и шириной a (рис.5.1, а). Под воздействием внешней силы пластина 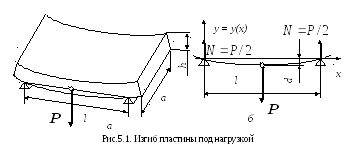искривляется и ее форма может быть описана функциейy(x) (рис. 5.1, б).

Определим величину и характер внутренних усилий, возникающих в пластине после того, как произошла деформация изгиба и установилось равновесие. Для этого выделим произвольный элемент пластины достаточно малой длины dl и запишем условия равновесия этой части, учитывая действие как внешних сил, так и внутренних усилий.

O′

П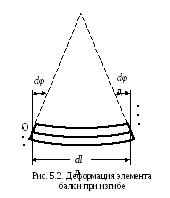ри изгибе этот выделенный элемент пластины деформируется примерно так, как изображено на рис. 5.2. Оба поперечных сечения сдвинулись на уголd. Слой, прилегающий к средней линии, является нейтральным. Укорочение (сжатие) и удлинение (растяжение) слоев, находящихся соответственно выше и ниже нейтрального слоя пропорционально расстоянию слоя от нейтрального, так как поперечное сечение и при деформации остается плоским. Тогда, еслиu– расстояние до некоторого слоя от нейтрали вверх, то напряжение в этом слое будет равно:

, (5.4)

где ₀– напряжение в самом удаленном слое, находящемся на расстоянииот нейтрального.

Таким образом, для пластины, ширина сечения которой равнаa, в слое толщинойduи находящемся на расстоянииuот нейтрали, имеет место усилие:

. (5.5)

Теперь можно подсчитать момент усилий в поперечном сечении:

Рис.5. 3. К выводу уравнения упругой линии

(5.6)

Величина 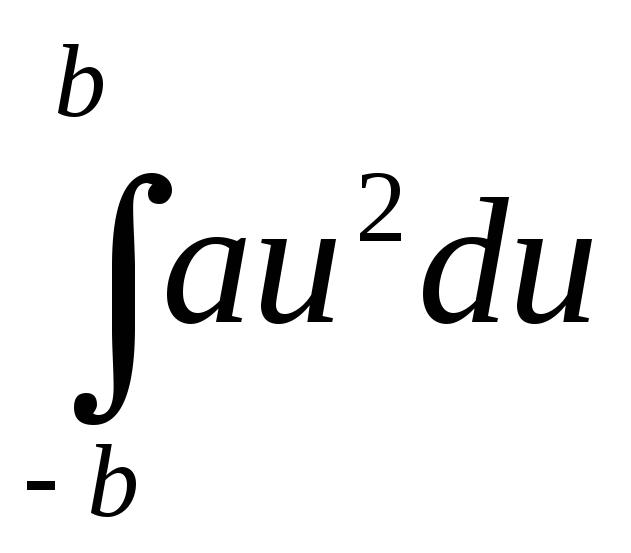, равная в данном случае, – коэффициент, определяемый геометрией пластины.

Деформация характеризуется формой линии изгиба, называемой упругой линией. В данном случае упругая линия проходит через ось пластины. Пусть уравнение искомой линии будет y=f(x), гдеy– отклонение точки с координатойxот прямой оси пластины, на которой лежали эти точки до деформации (рис. 5.3). Из рисунка видно, что, гдепредставляет собой угол, который составляет направление касательной к упругой линии в точке с координатойxс прямой осью. Если учесть, что углыочень малы, то, а изменение направления касательной при переходе от точкиx к точкеx+dxравно:.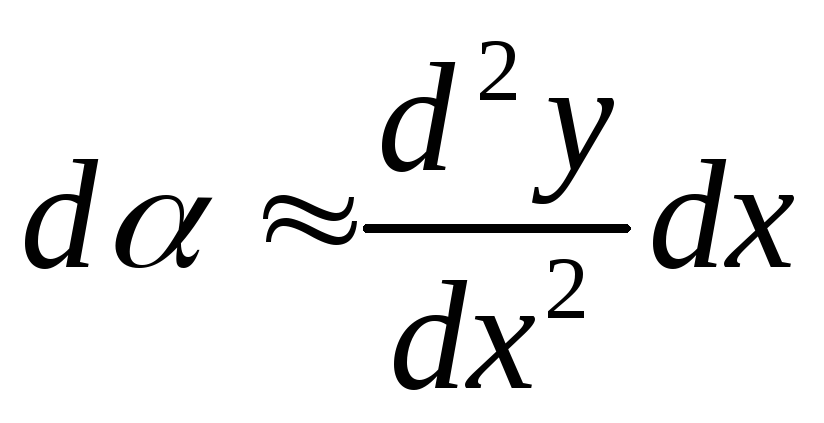

Так как поперечные сечения всегда перпендикулярны к упругой линии, то и, следовательно,

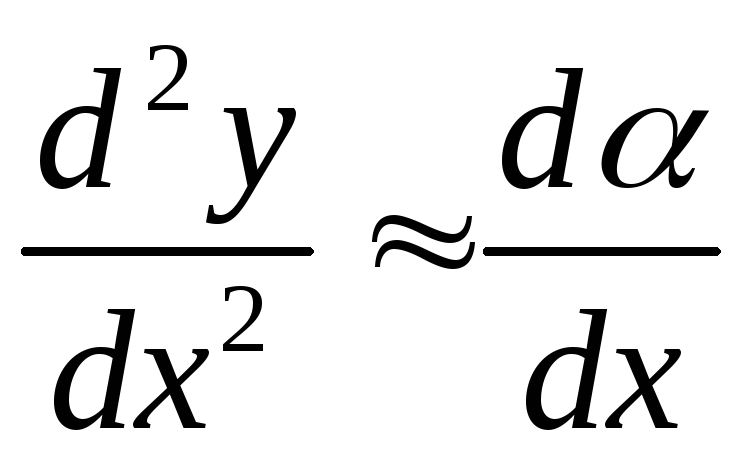. (5.7)

Момент усилий в поперечном сечении выражается согласно формуле (5.6). Максимальное напряжение ₀можно связать по закону Гука с деформацией слоя. Очевидно, что удлинение слоя, находящегося на расстоянииbот нейтрального, равно:

, (5.8)

а напряжение в нем:

. (5.9)

Учитывая (5.7), получаем:

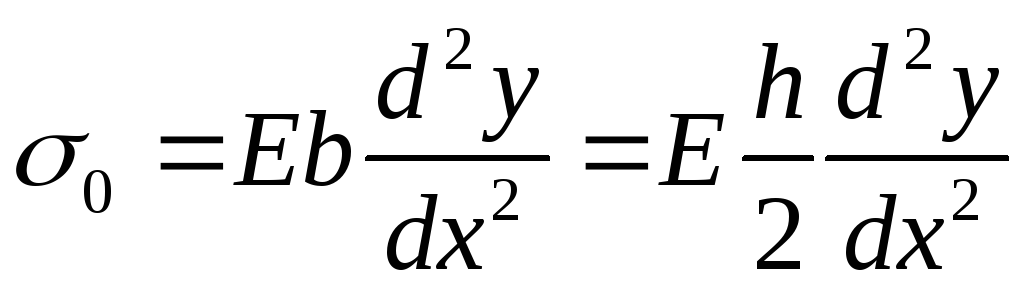. (5.10)

Теперь в уравнении (5.6) заменим по формуле (5.10) и найдем уравнение для упругой линии:

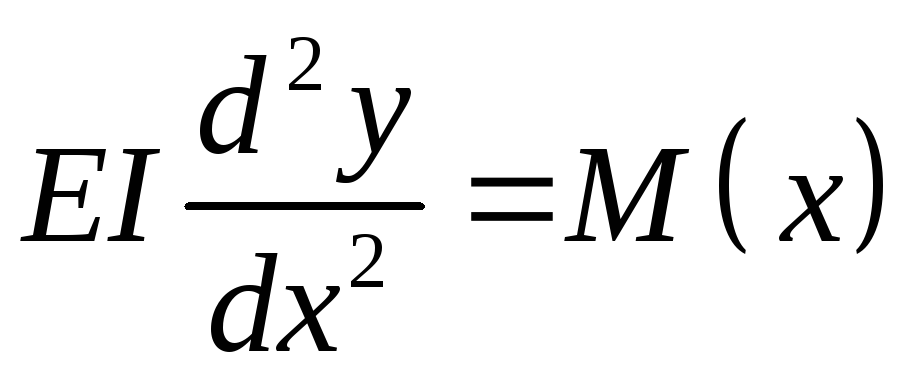. (5.11)

Таким образом, необходимо определить распределение изгибающих моментов M(x) вдоль оси пластины. Это можно сделать на основе заданной нагрузки и условий на опорах. Реакцию опор находим из условия равновесия всей пластины:. Изгибающий момент для сечения, расположенного на расстоянииот левой опоры должен быть уравновешен вращательным моментом реакции опоры, поэтому:

. (5.12)

В результате для формы упругой линии получаем дифференциальное уравнение:

, (5.13)

интегрируя которое, находим:

. (5.14)

Постоянную интегрирования Сопределим из условия равенства нулю наклона пластины в ее центре: то естьпри, откуда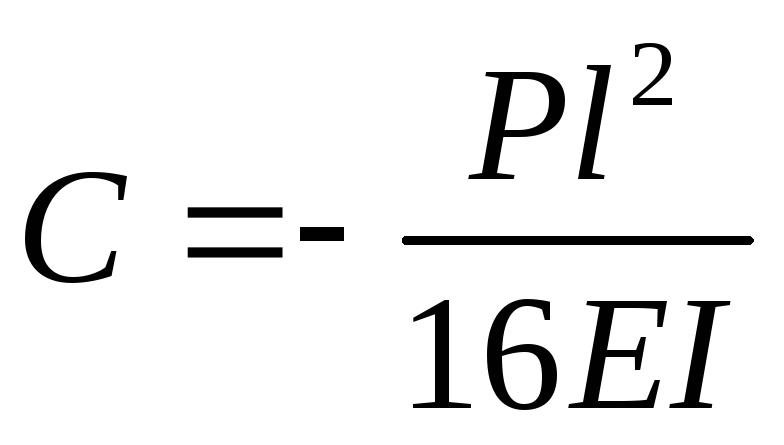. После второго интегрирования имеем:

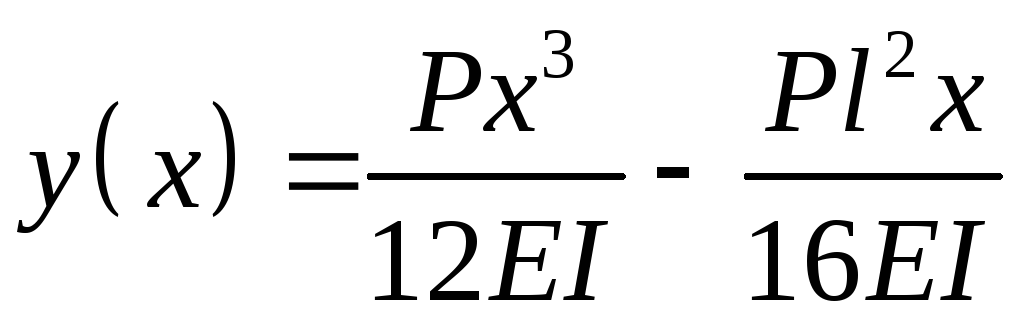. (5.15)

Вторая постоянная интегрирования равна нулю, так как y(0) = 0.

Стрела прогиба dпо модулю равна смещению середины пластины:

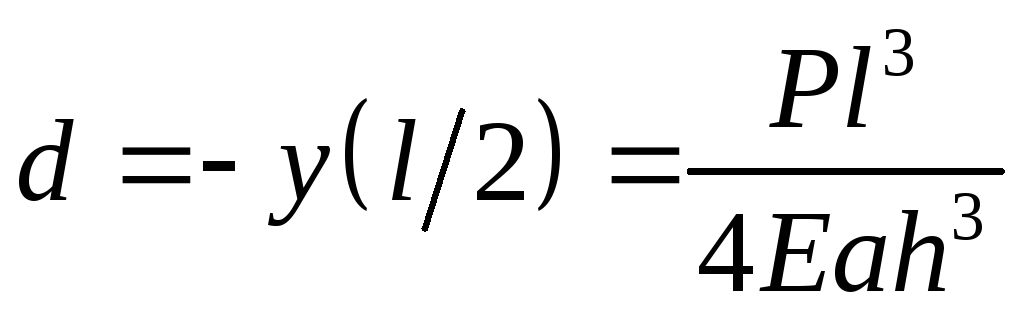, (5.16)

откуда окончательно для модуля Юнга получаем:

. (5.17)

Экспериментальная установка и методика измерений

Схема экспериментальной установки изображена на рис.5.4. Эксперимент проводится в такой последовательности.

1

1

. Установить одну из исследуемых пластин1 на призматические опоры 2. Установить часовой индикатор 3 таким образом, чтобы его наконечник коснулся пластины.

2

2

2

. Повесить на скобу4 гирю 5 массой m. По шкале индикатора определить величину прогиба. Для повышения точности повторить измерения 3 – 4 раза.

3

3

4

. Повторить задание п.2, увеличивая массу гири с помощью дополнительных грузов. Всего провести измерения для 6 ÷ 7 значенийm.

4

5

. Измерить штангенциркулем размеры пластины.

Обработка результатов экспериментов

1

Рис. 5. 4. Схема установки для определения модуля Юнга

. Вычислить среднее значение величины прогиба для каждого значения массы грузаm.

2. Построить график P = f(d).

3. Методом наименьших квадратов рассчитать значение тангенса угла наклона прямой P = f(d), используя формулу (П2.4) Приложения 2, в которой X_i = d_i, а Y_i = P_i, где d_i – среднее значение стрелы прогиба в i-м измерении, P_i = m_ig – нагрузка на пластину в этом измерении.

По формуле 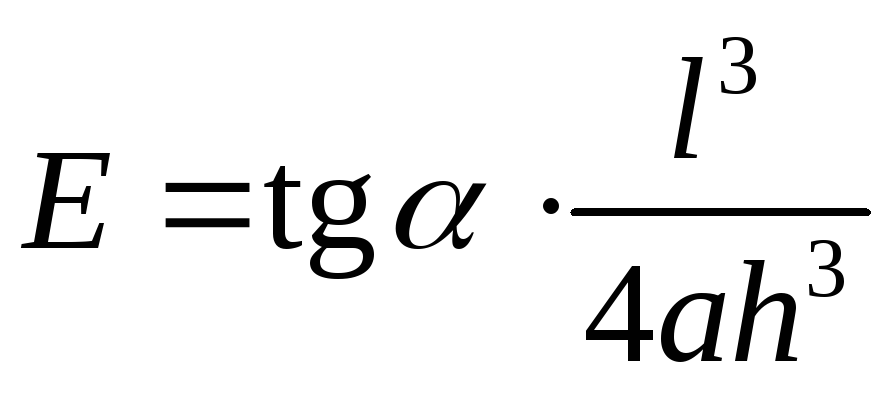вычислить среднее значение модуля Юнга для данного материала.

5. Сравнить полученное значение с приведенными в табл. 1 Приложения 1 и определить материал, из которого сделана исследуемая пластина.

Расчёт погрешностей

1. По формулам (П2.5), (П2.6) и (П2.8) Приложения 2 вычислить погрешность измерения (tg).

2. Определить случайную погрешность модуля Юнга по формуле:

. (5.18)

3. По формуле

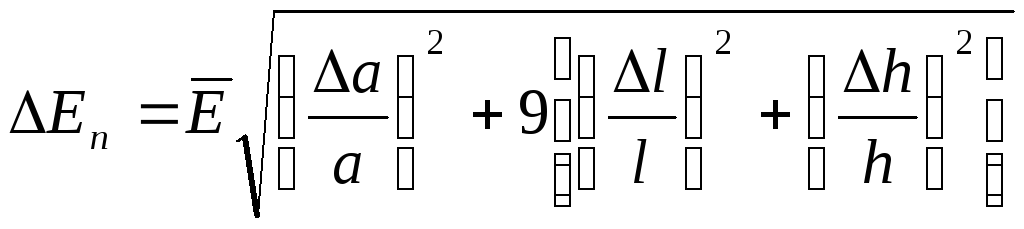(5.19)

вычислить приборную погрешность.

4. Результирующую погрешность вычислить по формуле (П2.11) Приложения 2.

5. Результат представить в виде:.

Лабораторная работа № 6

ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА

С ПОМОЩЬЮ ПРУЖИННОГО МАЯТНИКА

Цель работы:определение модуля сдвига материала пружины.

Основные теоретические сведения

Сдвигом называется деформация, при которой все плоские слои твердого тела, параллельные некоторой плоскости, называемой плоскостью сдвига, смещаются параллельно друг другу (рис.6.1). Сдвиг происходит под действием силы F, приложенной параллельно плоскости сдвига ВС. Мерой деформации при этом является угол сдвига , характеризующий относительный сдвиг. По закону Гука относительный сдвиг пропорционален касательному напряжению :

, (6.1)

где S– площадь грани ВС,G– модуль сдвига, численно равный касательному напряжению, вызывающему относительный сдвиг, равный единице.

Средние величины модуля сдвига некоторых материалов даны в табл. 2 Приложения 1.

В данной работе определяется модуль сдвига Gматериала, из которого изготовлена винтовая пружина. Основными геометрическими параметрами пружины являются диаметр проволокиd= 2r, диаметр витка пружиныD = 2Rи число витковN(рис. 6.2). Под действием растягивающей силыРдлина пружиныlувеличивается согласно закону Гука на величинуl:

, (6.2)

где – жесткость пружины.

Таким образом, необходимо по параметрам пружины вычислить зависимость между ее деформацией и силой.

Ограничимся рассмотрением винтовой пружины с малым шагом витков, то есть с малым по сравнению с ее диаметром расстоянием между смежными витками. При этом условии наклоном витков можно пренебречь и считать, что любое поперечное сечение параллельно силам Р, приложенным вдоль оси пружины и растягивающим ее. Можно показать, что для указанных условий жёсткость пружины

. (6.3)

Подставляя в формулу (6.2), получим:

. (6.4)

Из равенства (6.4) следует, что зависимость усилия растяжения от деформации имеет вид прямой:

. (6.5)

Тангенс угла наклона этой прямой к оси абсцисс

, (6.6)

откуда находим величину модуля сдвига:

. (6.7)

Если пружину заставить колебаться под действием груза массой mвдоль осиox, то получим пружинный маятник, уравнение незатухающих колебаний которого запишется так:

. (6.8)

Круговая частота незатухающих колебаний , откуда получим уравнение для периода:

. (6.9)

Подставляя выражение для k(6.3), получим формулу для вычисления модуля сдвига:

. (6.10)

Таким образом, по периоду колебаний пружинного маятника можно определить модуль сдвига.

Экспериментальная установка и методика измерений

Для определения модуля сдвига в работе используется установка, показанная на рис. 6.3. На штативе 1установлен кронштейн2с узлом крепления вертикально подвешенных сменных пружин3. К пружине подвешивается наборный груз4. Измерение периодов колебаний груза производится с помощью фотодатчика5. На данной установке можно измерить модуль сдвига двумя способами: с помощью пружинного маятника и методом растяжения пружины.