Individualnye_zadania / 3_VectAlg
.docФедеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Векторная алгебра
Индивидуальные задания
-
Пособие разработано доцентом Майзелес С. Б..
Одобрено методической комиссией кафедры «Высшая математика»
© 2007, каф. «Высшая математика» ПГТУ
Пермь 2007
Образец решения варианта
Задание 1.
Коллинеарны ли векторы
и
,
разложенные по векторам
и
,
где
Решение:
1. Вычислим проекции векторов
:
2. Два вектора коллинеарны, если их проекции пропорциональны, следовательно, проверим пропорциональность проекций векторов:
не коллинеарны.
Задание 2.
Перпендикулярны ли векторы
?
Решение:
Два вектора перпендикулярны, если их скалярное произведение равно 0, вычислим скалярное произведение:
векторы
не перпендикулярны.
Задание 3.
Компланарны ли векторы
?
Решение:
Три вектора компланарны, если смешанное произведение векторов равно 0, вычислим смешанное произведение векторов:
векторы
не компланарны.
Задание 4.
Найти угол между векторами
где
Решение:
Косинус угла между векторами вычисляется по формуле:
Задание 5.
Даны точки:
Найти:
1. пр
;
2. пр
;
3.
;
4.
;
5.
;
6.
;
7.
;
8.
;
9.
;
10.
;
11.
;
12. орт вектора
.
Решение:
1. Проекция вектора на вектор вычисляется по формуле:
пр
находим проекции векторов:
вычисляем скалярное произведение векторов и длину вектора:
пр
2. Находим проекции векторов:
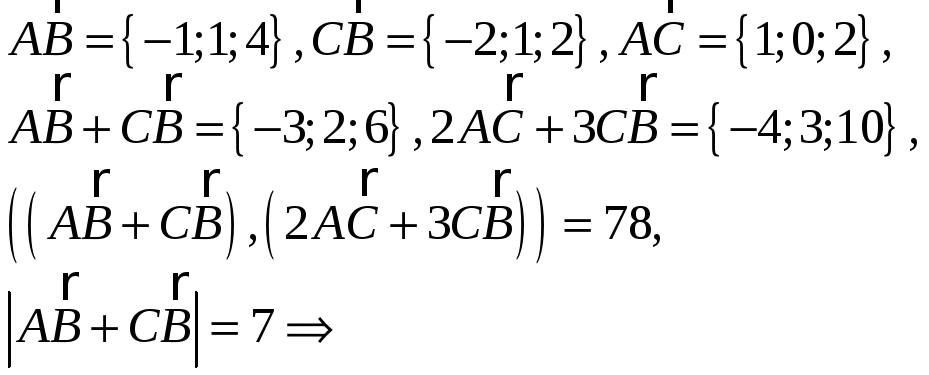
пр
;
3. Находим проекции векторов:
;
4. Находим проекции векторов:
;
5.
;
6.
7. Векторное произведение векторов
вычисляется по формуле:
где
;
8.
;
9. Смешанное произведение векторов
вычисляется по формул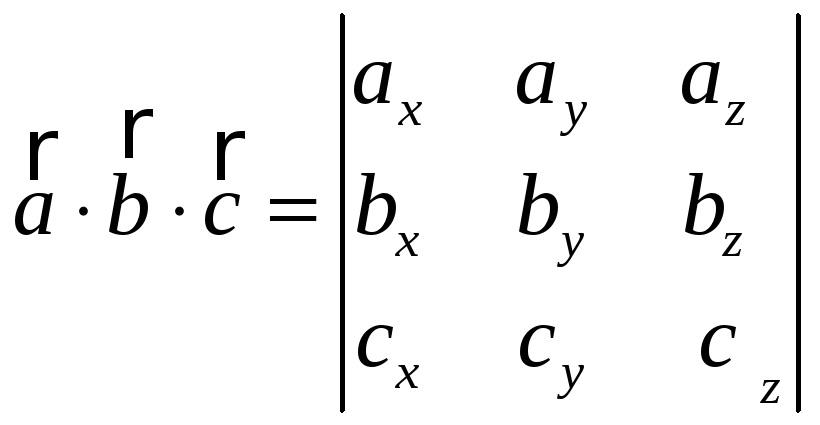е:
,
где
;
10.
;
11.
;
12. Орт вектора
,
так как орт- это вектор единичной длины
необходимо каждую проекцию вектора разделить на его длину.
Задание 6.
Даны координаты вершин пирамиды:
Вычислить:
1. объем пирамиды;
2. длину ребра
;
3. площадь грани
;
4. угол между ребрами
и
.
Решение:
1. Объем пирамиды вычисляется по
формуле:
;
2. Длина ребра
;
3. Площадь грани
вычисляется по формуле:
;
4. Угол между ребрами
и
вычисляется по формуле:
Задание 7.
Имеет ли смысл выражение
?
Обосновать.
Решение:
Выражение
смысла не имеет, так как складывать
числа с векторами нельзя: в результате
скалярного призведения
получим число, затем мы должны сложить
вектор
с результатом скалярного произведения
(число), что не возможно.
Задание 8.
Придумать исходные данные на указанные типы задач векторной алгебры и решить их.
Решение:
Рассмотрим одну из указанных задач, например, задачу 8,3:
Дано:
тупой,
<0,
Найти:
.
Решение:
По условию:
Итак, получили систему трех уравнений с тремя неизвестными, решением которой и будут проекции исходного вектора:
по
формулам Крамера находим отношение
коэффициентов:
.
Условие
выполняется при
то есть
Ответ:
Второй способ решения:
По условию:
Найденные значения
подставим в условие
,
найдем
так, что бы
.
Итак:
Так как по условию
то
Итак:
Ответ:
Задания для индивидуальной контрольной работы
Задание 1
Коллинеарны ли векторы
и
,
разложенные по векторам
и
?
Задание 2
Перпендикулярны ли векторы
и
?
Задание 3
Компланарны ли векторы
?
Задание 4
Найти угол между векторами
и
.
Задание 5
Даны координаты точек
Вычислить:
1) пр
;
2) пр
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12) орт вектора
;
Задание 6
Даны координаты вершин пирамиды
.
Вычислить:
1) объем пирамиды;
2) длину ребра
;
3) площадь грани
;
4) угол между ребрами
и
;
Задание 7
Имеет ли смысл выражение ? Обосновать.
Задание 8
Придумать исходные данные на указанные типы задач векторной алгебры и решить их.
8.1 Дано:
острый
(или с любой другой осью, тупой или
острый),
,
где
произвольное
число.
Найти:
8.2 Дано:
.
Найти:
8.3 Дано:
тупой(острый
или с любой другой осью),
Найти:
8.4 Дано:
(любой
другой оси),
Найти:
8,5 Дано:
,
где
произвольные
числа.
Найти:
Варианты для индивидуальной контрольной работы.
ВАРИАНТ 1
1.1
2.1
3.1
4.1
5.1
6.1
7.1
ВАРИАНТ 2
1.2
2.2
3.2
4.2
5.2
6.2
7.2
ВАРИАНТ 3
1.3
2.3
3.3
4.3
5.3
6.3
7.3
ВАРИАНТ 4
1.4
2.4
3.4
4.4
5.4
6.4
7.4
ВАРИАНТ 5
1.5
2.5
3.5
4.5
5.5
6.5
7.5
ВАРИАНТ 6
1.6
2.6
3.6
4.6
5.6
6.6
7.6
ВАРИАНТ 7
1.7
2.7
3.7
4.7
5.7
6.7
7.7
ВАРИАНТ 8
1.8
2.8
3.8
4.8
5.8
6.8
7.8
ВАРИАНТ 9
1.9
2.9
3.9
4.9
5.9
6.9
7.9
ВАРИАНТ 10
1.10
2.10
3.10
4.10
5.10
6.10
7.10 пр
ВАРИАНТ 11
1.11
2.11
3.11
4.11
5.11
6.11
7.11 пр
ВАРИАНТ 12
1.12
2.12
3.12
4.12
5.12
6.12
7.12 пр
ВАРИАНТ 13
1.13
2.13
3.13
4.13
5.13
6.13
7.13 пр
ВАРИАНТ 14
1.14
2.14
3.14
4.14
5.14
6.14
7.14 пр
ВАРИАНТ 15
1.15
2.15
3.15
4.15
5..15
6.15
7.15 пр
ВАРИАНТ 16
1.16
2.16
3.16
4.16
5.16
6.16
7.16 пр
ВАРИАНТ 17
1.17
2.17
3.17
4.17
5.17
6.17
7.17 пр
ВАРИАНТ 18
1.18
2.18
3.18
4.18
5.18
6,18
7.18 пр
ВАРИАНТ 19
1.19
2.19
3.19
4.19
5.19
6.19
