
- •Пермь 2007 Вариант решения заданий
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции .
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции .
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции .
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции .
-
Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
-
Найти производную сложной функции
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
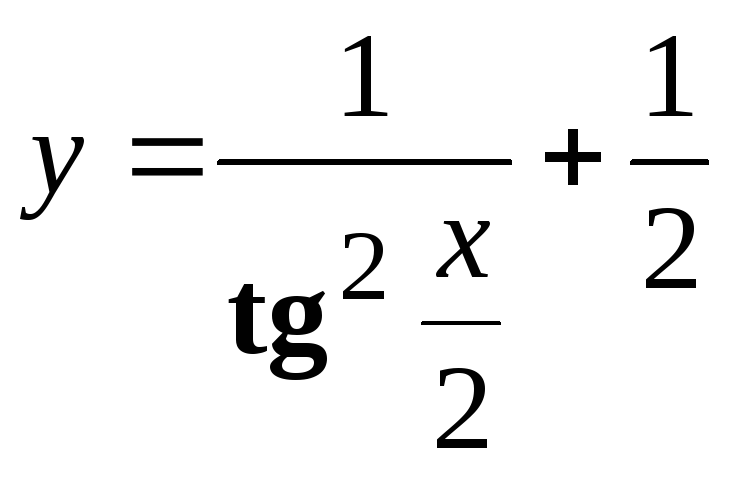
![]()
![]()
-
Найти

![]()
![]()
![]()

-
Показать, что функция
 удовлетворяет
уравнению
удовлетворяет
уравнению

-
Найти

а)
![]() в)
в)
![]()
б)

-
Найти уравнения касательной и нормали к кривой
 в точке М(-2,
3).
в точке М(-2,
3). -
Для функций
 проверить выполнение условий теоремы
Коши на отрезке [1, 2] и найти соответствующее
значение .
проверить выполнение условий теоремы
Коши на отрезке [1, 2] и найти соответствующее
значение .
Вариант 14
-
Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
-
Найти производную сложной функции
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
Найти

![]()
![]()
![]()

-
Показать, что функция
 удовлетворяет
уравнению
удовлетворяет
уравнению

-
Найти

а)
![]() в)
в)
![]()
б)

-
В точках пересечения прямой
 и параболы
и параболы
 проведены нормали к параболе.
Написать уравнения этих нормалей.
проведены нормали к параболе.
Написать уравнения этих нормалей. -
Функция
 принимает равные
значения на концах отрезка [-а, а].
Убедиться в том, что производная от
этой функции нигде в интервале (-а, а)
в нуль не обращается, и объяснить такое
уклонение от теоремы Ролля.
принимает равные
значения на концах отрезка [-а, а].
Убедиться в том, что производная от
этой функции нигде в интервале (-а, а)
в нуль не обращается, и объяснить такое
уклонение от теоремы Ролля.
Вариант 15
-
Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
-
Найти производную сложной функции
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


-
Найти

![]()
![]()
![]()

-
Показать, что функция
 удовлетворяет уравнению
удовлетворяет уравнению

-
Найти

а)
![]() в)
в)
![]()
б)

-
Показать, что касательные к гиперболе
 в точках ее пересечения с осями координат
параллельны
между собой.
в точках ее пересечения с осями координат
параллельны
между собой. -
Проверить справедливость теоремы Ролля для функции
 на отрезке [1, 2]. Если да, найти
соответствующее значение .
на отрезке [1, 2]. Если да, найти
соответствующее значение .
Вариант 16
-
Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
-
Найти производную сложной функции
![]()
![]()
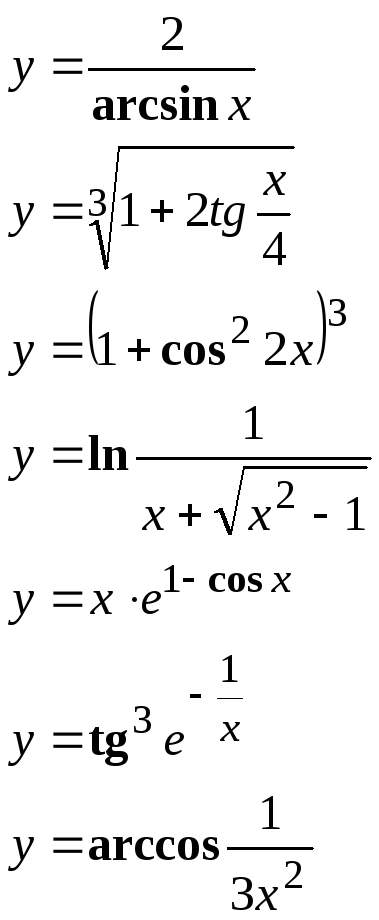

-
Найти

![]()
![]()
![]()

-
Показать, что функция
 удовлетворяет уравнению
удовлетворяет уравнению

-
Найти
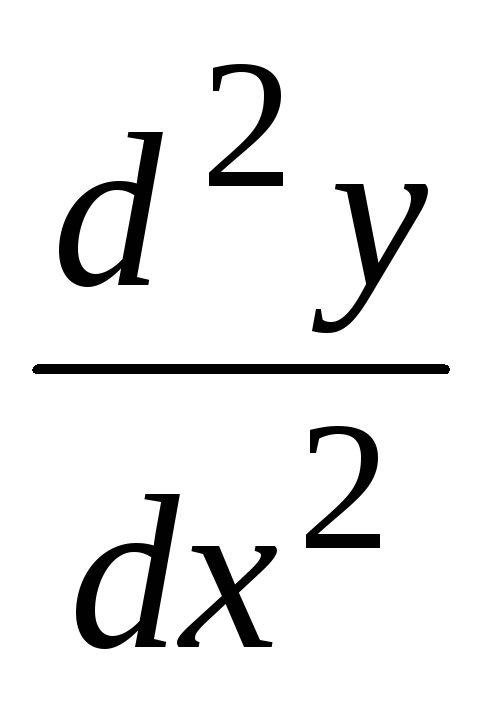
а)
![]() в)
в)
![]()
б)
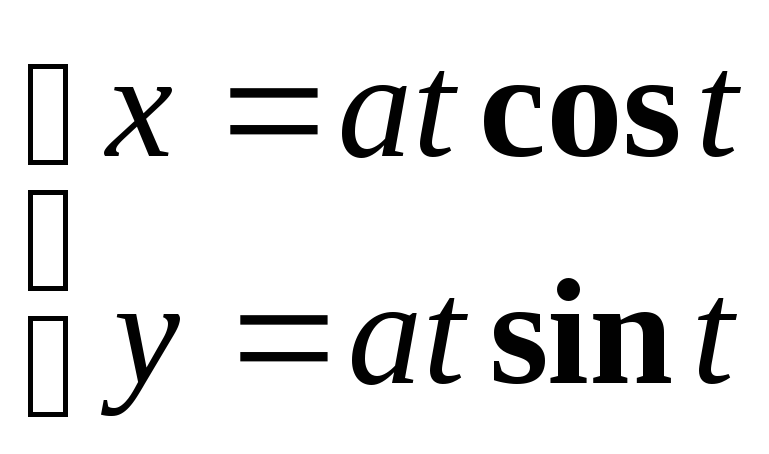
-
Составить уравнение такой нормали к параболе
 ,
которая перпендикулярна к прямой,
соединяющей начало координат с вершиной
параболы.
,
которая перпендикулярна к прямой,
соединяющей начало координат с вершиной
параболы. -
Проверить справедливость теоремы Ролля для функции
 на отрезке [1, 2]. Если да, найти
соответствующее значение .
на отрезке [1, 2]. Если да, найти
соответствующее значение .
Вариант 17
-
Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
-
Найти производную сложной функции
![]()
![]()

![]()

-
Найти

![]()
![]()
![]()

-
Показать, что функция
 удовлетворяет уравнению
удовлетворяет уравнению

-
Найти

а)
![]() в)
в)
![]()
б)

-
Составить уравнение нормали к графику функции
 в
точке пересечения с биссектрисой
первого координатного угла.
в
точке пересечения с биссектрисой
первого координатного угла. -
Построить график функции
 отрезке [0, 3] . Почему здесь нельзя
провести касательную, параллельную
хорде? Какое из условий теоремы Лагранжа
здесь не выполнено?
отрезке [0, 3] . Почему здесь нельзя
провести касательную, параллельную
хорде? Какое из условий теоремы Лагранжа
здесь не выполнено?
Вариант 18
-
Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
-
Найти производную сложной функции
![]()
![]()


-
Найти

![]()
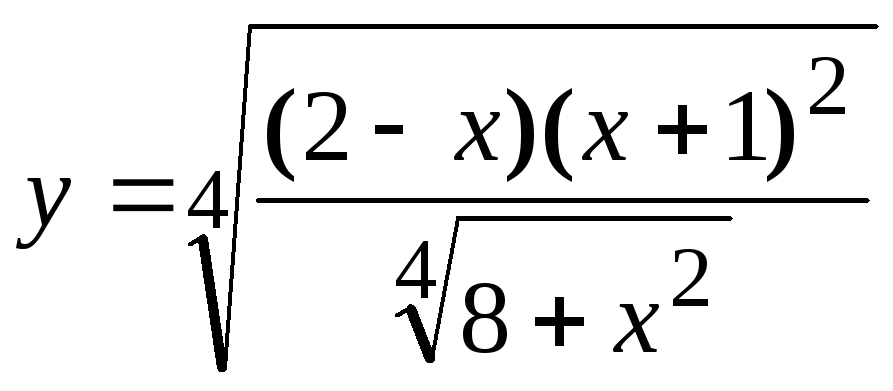
![]()

-
Показать, что функция
 удовлетворяет
уравнению
удовлетворяет
уравнению

-
Найти

а)
![]() в)
в)
![]()
б)
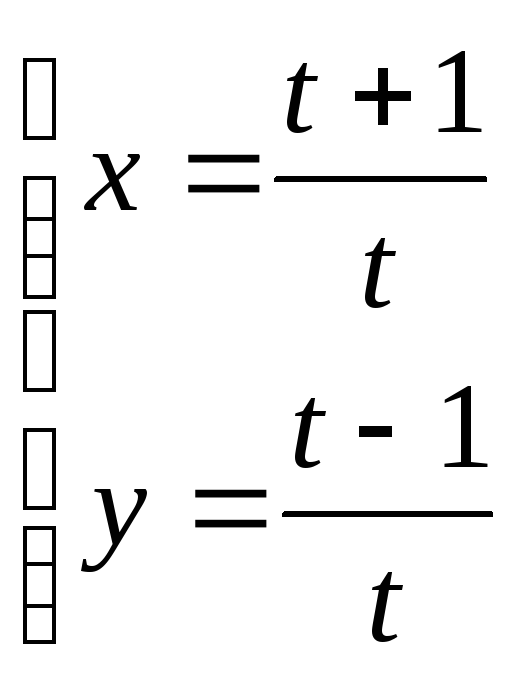
-
В каких точках кривой
 касательная
параллельна прямой
касательная
параллельна прямой
 ?
? -
Функция
 обращается в нуль на концах отрезка
[-1, 1]. Убедиться в том, что производная
от этой функции нигде в интервале (-1,
1) в нуль не обращается. Объяснить,
почему здесь неприменима теорема
Ролля.
обращается в нуль на концах отрезка
[-1, 1]. Убедиться в том, что производная
от этой функции нигде в интервале (-1,
1) в нуль не обращается. Объяснить,
почему здесь неприменима теорема
Ролля.
Вариант 19
