
- •Пермь 2007 Вариант решения заданий
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции .
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции .
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции .
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции .
-
Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
-
Найти производную сложной функции
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
Найти

![]()
![]()
![]()

-
Показать, что функция
 удовлетворяет уравнению
удовлетворяет уравнению

-
Найти

а)
![]() в)
в)
![]()
б)
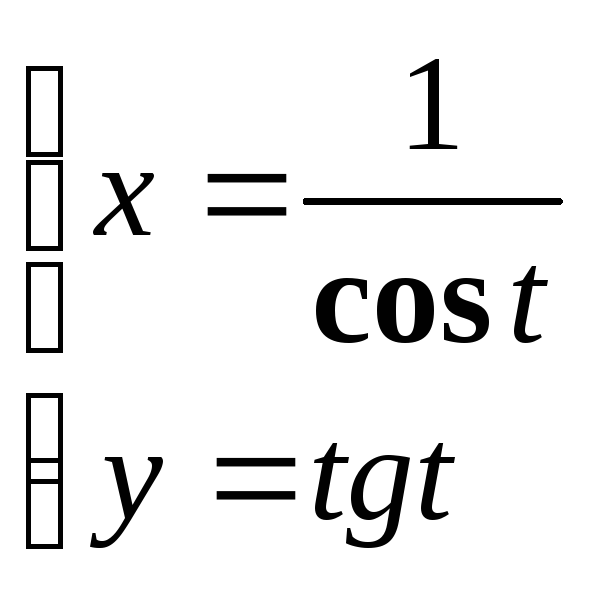
-
Написать уравнения касательной и нормали в точке (2, 2) к кривой

-
Дана функция
 .
Пусть
.
Пусть
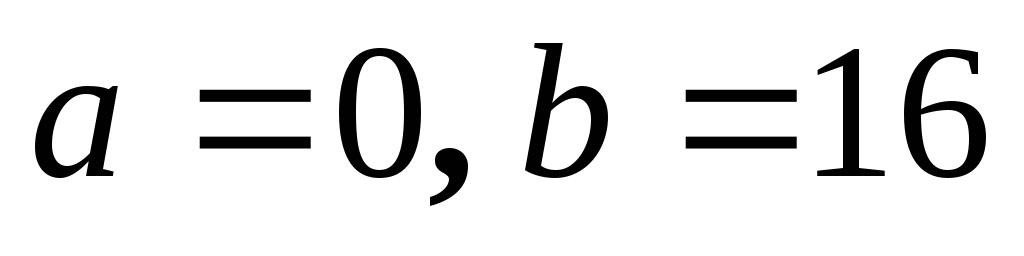 .
Тогда
.
Тогда
 .
Однако производная
.
Однако производная
 не
обращается в нуль ни в одной точке
интервала
(0,16). Противоречит ли это теореме Ролля?
не
обращается в нуль ни в одной точке
интервала
(0,16). Противоречит ли это теореме Ролля?
Вариант 8
-
Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
-
Найти производную сложной функции
![]()
![]()

![]()
![]()
![]()
![]()
![]()

![]()
![]()

![]()
![]()
![]()
![]()
-
Найти

![]()
![]()
![]()

-
Показать, что функция
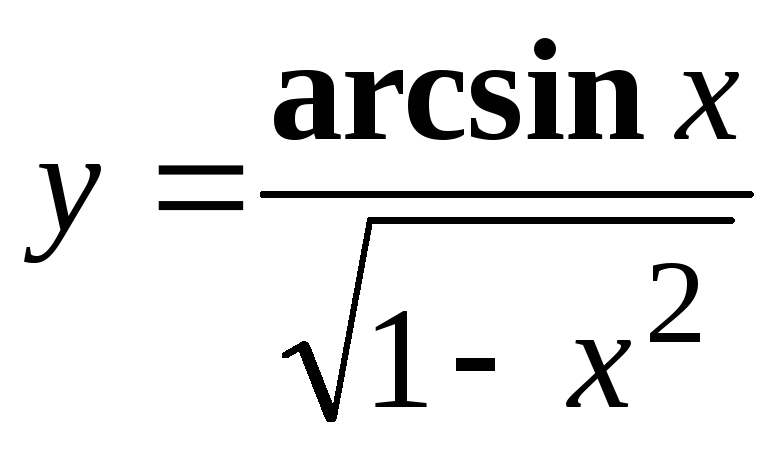 удовлетворяет
уравнению
удовлетворяет
уравнению

-
Найти

а)
![]() в)
в)
![]()
б)
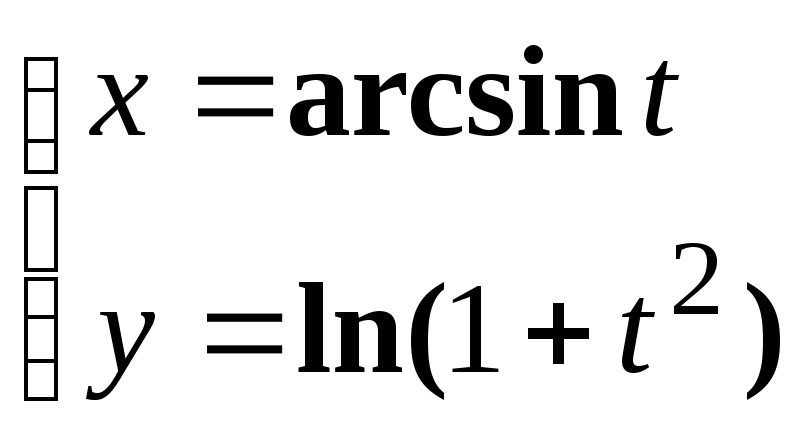
-
Написать уравнения касательной и нормали к кривой
 в
точке (1, 2).
в
точке (1, 2). -
Удовлетворяют ли функции
 условиям
теоремы Коши на отрезке [-3, 3].
условиям
теоремы Коши на отрезке [-3, 3].
Вариант 9
-
Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
-
Найти производную сложной функции
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
Найти

![]()
![]()
![]()

-
Показать, что функция
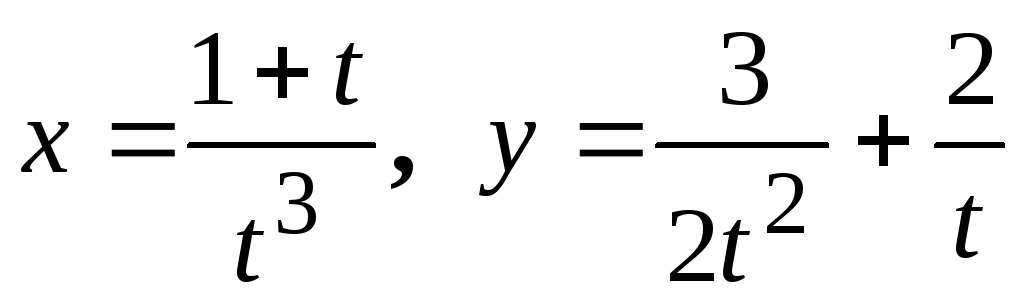 удовлетворяет
уравнению
удовлетворяет
уравнению

-
Найти

а)
![]() в)
в)
![]()
б)

-
В какой точке кривой
 касательная
перпендикулярна
к прямой
касательная
перпендикулярна
к прямой
 .
. -
Проверить, применима ли теорема Лагранжа к функции
 на отрезке [0, 1]. Если да,
найти соответствующее значение .
на отрезке [0, 1]. Если да,
найти соответствующее значение .
Вариант 10
-
Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
-
Найти производную сложной функции
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
Найти

![]()

![]()

-
Показать, что функция
 удовлетворяет
уравнению
удовлетворяет
уравнению
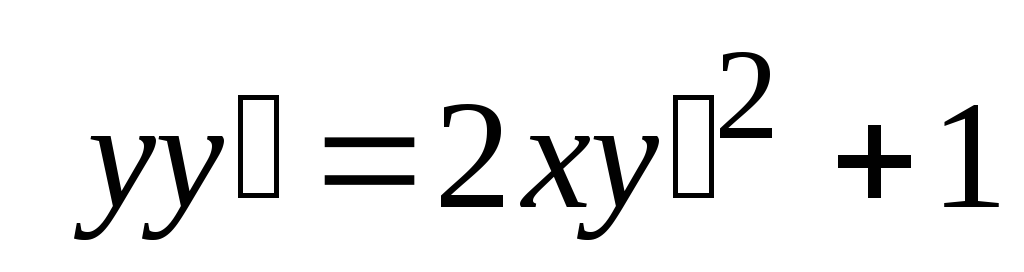
-
Найти

а)
![]() в)
в)
![]()
б)

-
Какой угол образует с осью абсцисс касательная к параболе
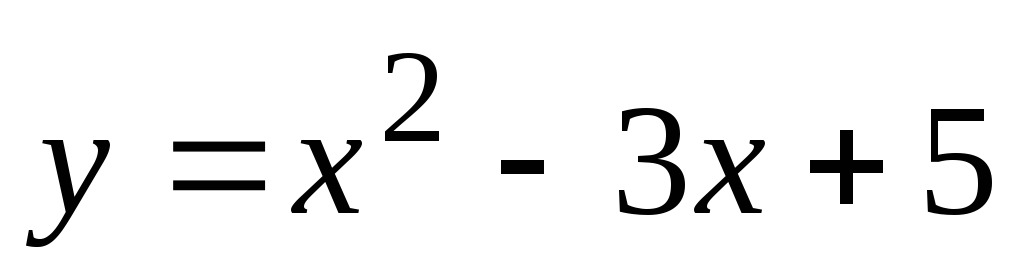 ,
проведенная
в точке с ординатой
,
проведенная
в точке с ординатой
 ?
Написать уравнения этой касательной
и
нормали.
?
Написать уравнения этой касательной
и
нормали. -
Для функций
 проверить
выполнение условий теоремы Коши на
отрезке
[
проверить
выполнение условий теоремы Коши на
отрезке
[ ]
и найти соответствующее .
]
и найти соответствующее .
Вариант 11
-
Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
-
Найти производную сложной функции
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
Найти

![]()

![]()

-
Показать, что функция
 удовлетворяет
уравнению
удовлетворяет
уравнению

-
Найти

а)
![]() в)
в)
![]()
б)

-
На кривой
 найти точки, в которых касательная
перпендикулярна к прямой
найти точки, в которых касательная
перпендикулярна к прямой
 .
. -
Проверить, что между корнями функции
 находится корень ее производной.
Пояснить
графически.
находится корень ее производной.
Пояснить
графически.
Вариант 12
-
Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
-
Найти производную сложной функции
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
Найти

![]()
![]()
![]()

-
Показать, что функция
 удовлетворяет
уравнению
удовлетворяет
уравнению
![]()
-
Найти

а)
![]() в)
в)
![]()
б)

-
Найти угловой коэффициент касательной к кривой
 в
точке М(2,-1).
в
точке М(2,-1). -
Проверить, применима ли теорема Лагранжа к функции
 на отрезке
на отрезке
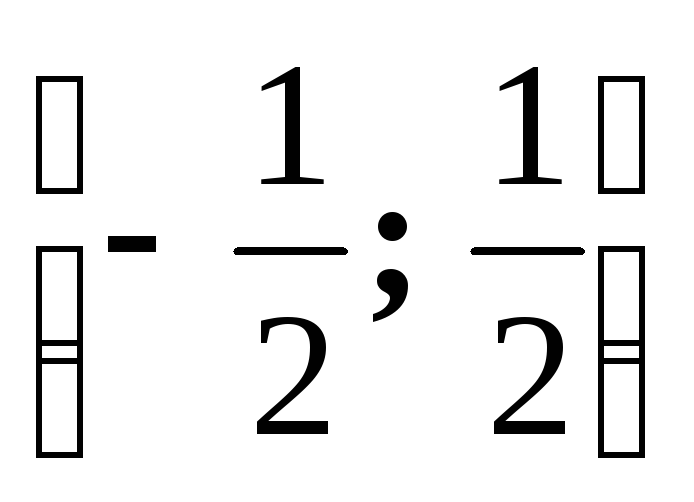 .
.
Вариант 13
