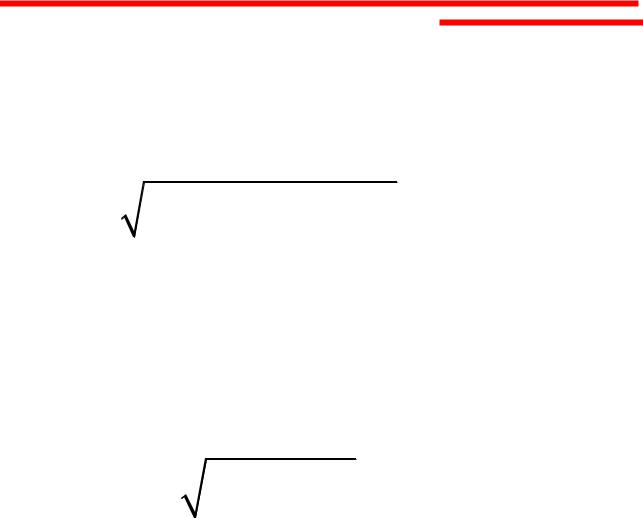
Площадь поверхности вращения
Если кривая задана параметрическими уравнениями
|
x x(t), |
y y(t), |
|
t1 t t2 |
|
|
||
|
t2 |
|
|
2 |
|
2 |
|
|
|
Sx 2 y(t) |
dt. |
|
|||||
|
(x (t)) |
|
( y (t)) |
|
|
|||
|
t1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если дуга задана в полярных координатах
|
r r( ), |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
Qx 2 r sin |
r |
d |
|
||||
|
|
(r ) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
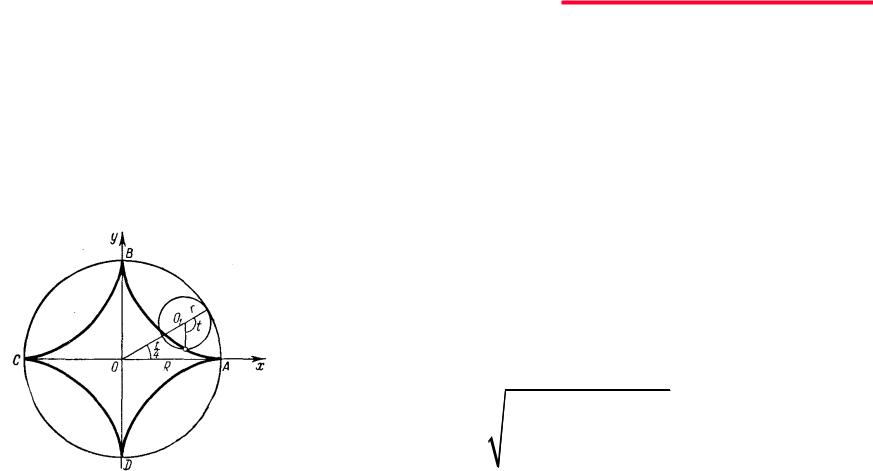
Пример:
Найти площадь поверхности, образованной вращением астроиды
|
x2 / 3 y2 / 3 |
a2 / 3 |
вокруг оси Ox |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
||
, |
|
|
|
|
|
|
y (a2 / 3 x2 / 3)3 / 2 , |
|||||||||
, |
|
|
|
|
|
|
|
|
|
|
|
a2 / 3 x2 / 3 1/ 2 |
||||
, |
|
|
|
|
3 2 / 3 |
, |
2 / 3 1/ 2 2 1/ 3 |
|
|
|
||||||
|
|
|
(a |
x |
) x |
|
|
|
|
|
|
|||||
|
|
|
y |
1/ 3 |
||||||||||||
. |
|
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
1 a2 / 3 x2 / 3 |
|
a1/ 3 . |
|||||||
|
|
|
|
|
|
|
x2 / 3 |
|
|
|
|
x |
|
1/ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,
,
,
.
Пример:
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 / 3 |
x |
2 / 3 |
|
|
1/ 3 |
|
|
|
||||||||
|
Sx 2 y |
1 |
( yx )2 dx |
|
|
1 ( yx )2 1 a |
|
|
|
|
|
|
|
|
|
a |
|
. |
|
|
|||||||||||||||
|
|
|
|
x2 / 3 |
|
|
|
|
|
|
x |
|
1/ 3 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
a |
|
2 / 3 |
|
2 / 3 |
|
3/ 2 |
|
1/ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Qx 2 2 (a |
x |
) |
a |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
x1/ 3 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 3 a |
(a |
2 / 3 |
x |
2 / 3 |
) |
3/ 2 |
x |
1/ 3 |
dx |
|
|
|
|
|
|||||||||||||||
|
|
|
|
4 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 3 |
3 (a2 / 3 |
x2 / 3)5 / 2 |
|
a |
12 |
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
. |
|||||
|
|
|
|
|
|
|
|
|
4 a |
|
|
|
|
5/ 2 |
|
|
|
|
|
|
5 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
? 2 Механическое приложение
Пройденный путь
Путь, пройденный точкой за промежуток времени [t0, T], равен
соответствующему определенному интегралу от скорости движения точки
T
s v(t)dt
t0
Замечание:
Результат верен лишь в том случае, если скорость v=f(t) не меняет знака, например, f(t) 0. Если же скорость v меняет знак, то указанная выше формула дает приращение абсциссы движущейся точки за промежуток времени [t0, T].
Работа
Работа, произведенная силой F при перемещении точки М из положения s=a в положение s=b, равна соответствующему определенному интегралу от силы:
b
A F(s)ds
a
Масса стержня переменной плотности
Будем считать, что отрезок [a ,b] оси х имеет массу с переменной линейной плотностью (х) 0,
где (х) – непрерывная на [a ,b] функция. Общая масса этого отрезка:
b
M (x)dx
a
? 3 Приближенное вычисление
Понятие о приближенном вычислении определенных интегралов
|
b |
y ( x ) |
f (x)dx |
|
|
|
a |
|
|
|
|
y |
= f ( x ) |
|
|
|
|
|
|
|
|
|
|
h b |
a |
|
y 0 |
y 1 |
y 2 |
y i |
y i + 1 |
y n |
n |
|
|
|
|
|
|
h |
|
|
|
0 |
а = ах 0 |
x 1 |
x 2 |
x i |
x i + 1 |
x n b= b |
х |
|
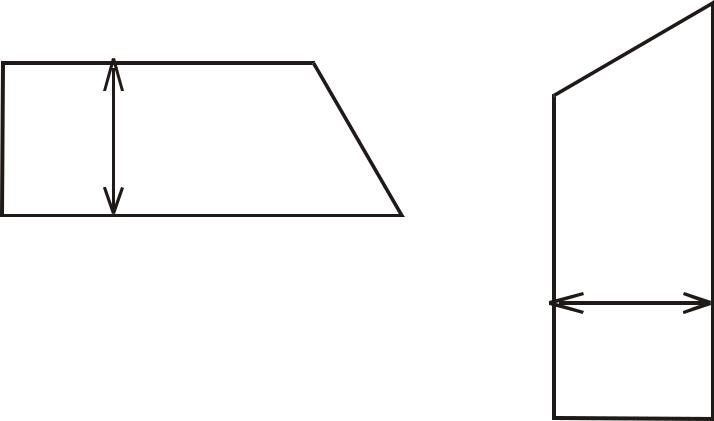
Понятие о приближенном вычислении определенных интегралов
y i
h
y i + 1 |
y i |
h |
y |
i + 1 |
|
|
|
|
S h2 ( yi yi 1 )
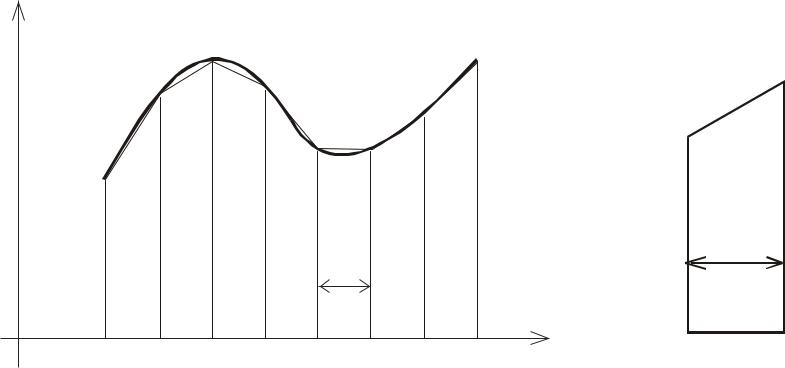
y ( x )
|
|
|
|
y |
= |
f ( |
x |
) |
|
|
|
|
|
|
y 0 |
y 1 |
y 2 |
y i |
|
y i + 1 |
y n |
y i |
h |
y |
i + 1 |
||
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
а = х 0 |
x 1 |
x 2 |
x i |
|
|
|
x i + 1 |
x n = b |
х |
|
|
|
b |
|
( y0 y1 ) h |
|
y2 ) ... h |
|
|
|||
f (x)dx h |
( y1 |
( yn 1 yn ) |
|||||||
a |
2 |
|
|
2 |
|
2 |
|
|
|
|
b |
|
y0 |
|
|
|
|
yn |
|
|
|
|
|
|
|
||||
|
f (x)dx h |
|
y1 |
y2 ... yn 1 |
|
|
|
||
|
2 |
|
|
||||||
|
a |
|
|
|
|
|
2 |
||
1
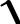
1 x2 dx
0
h=0,1
i |
xi |
yi |
|
0 |
|||
0,0 |
1,0000 |
||
1 |
0,1 |
1,0050 |
|
2 |
0,2 |
1,0198 |
|
3 |
0,3 |
1,0440 |
|
4 |
0,4 |
1,0770 |
|
5 |
0,5 |
1,1180 |
|
6 |
0,6 |
1,1662 |
|
7 |
0,7 |
1,2207 |
|
8 |
0,8 |
1,2806 |
|
9 |
0,9 |
1,3454 |
|
10 |
1,0 |
1,4142 |
1 |
|
|
|
|
|
|
1,0000 |
|
1,4142 |
|
|
|
1 x |
2 |
dx 0,1 |
1,0050 1,0198 ... 1,3454 |
|
||||||
|
|
|
|
|
|||||||
|
|
|
2 |
2 |
|
||||||
0 |
|
|
|
|
|
|
|
|
|
||
0,1 11,4838 1,148
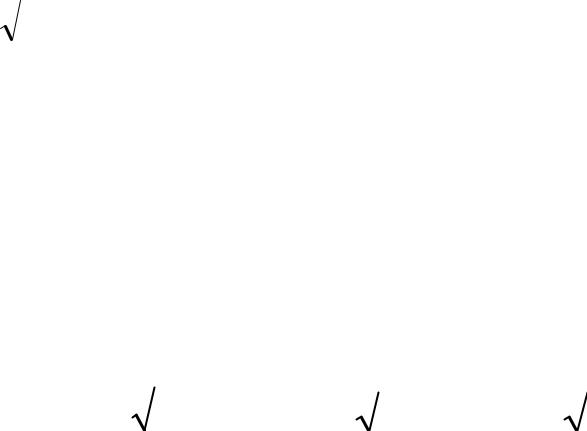
1 |
|
|
|
|
|
|
1,0000 |
|
1,4142 |
|
|
|
1 x |
2 |
dx 0,1 |
1,0050 1,0198 ... 1,3454 |
|
||||||
|
|
|
|
|
|||||||
|
|
|
2 |
2 |
|
||||||
0 |
|
|
|
|
|
|
|
|
|
||
0,1 11,4838 1,148
1 |
|
|
1 |
|
|
1 ln(1 |
|
|
1 x2 dx |
|
|
|
) 1,1479 |
||||
2 |
2 |
|||||||
0 |
|
|
2 |
|
|
2 |
|
|