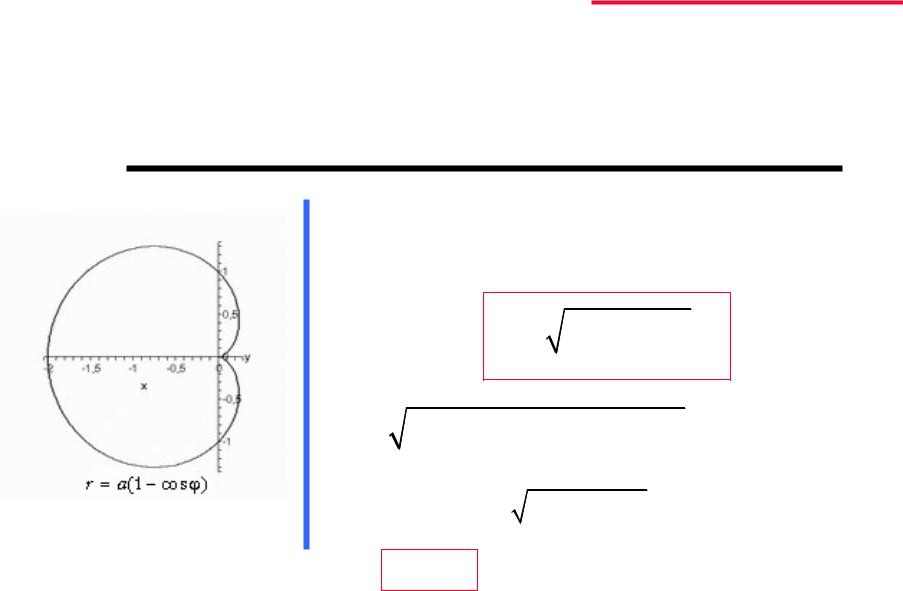
Пример:
Найти длину кардиоиды
r a(1 cos ) |
(a 0). |
,
1 l
2 0
.
Решение:
r asin
|
|
2 |
|
2 |
|
|
l |
|
d |
||||
|
( ) |
|
a2 (1 cos )2 a2 sin2 d
|
|
d 4a, |
a |
2(1 cos )d 2a sin |
|
0 |
0 |
2 |
l 8a
? 1.3 Объем тела
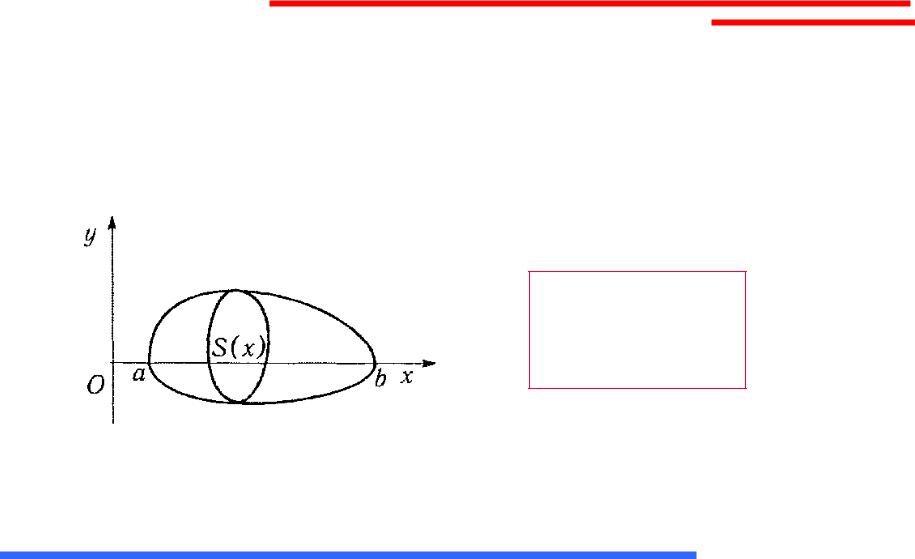
Объем тела по площадям его параллельных сечений
Если площадь S(x) сечения тела плоскостью, перпендикулярной оси Ох, является непрерывной функцией на отрезке [a, b], то объем тела:
b
V S(x)dx
a
где а, b – левая и правая границы тела.
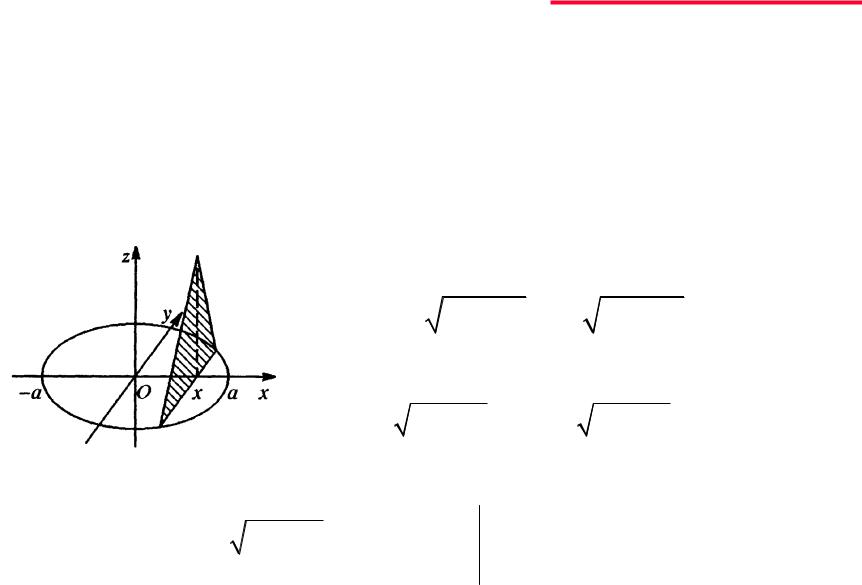
Пример:
Найти объем тела, основание которого – круг радиуса а, а сечение плоскостью, перпендикулярной фиксированному диаметру круга, есть равнобедренный треугольник высоты h.
,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
, |
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|||||||||
|
|
|
|
|
|
x2 y2 a2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
, |
|
|
|
|
|
|
|
|
|
|
|
|
V S(x)dx |
|
|||||||||||
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
, |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(x) |
2 a2 |
|
x2 h h a2 x2 |
( a x a) |
||||||||||||||||
. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
a2 x2 dx |
||||||
|
|
|
|
|
|
|
V h |
|
a2 x2 dx 2h |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
2 |
|
2 |
|
a2 |
|
|
x |
a |
|
|
a2 |
1 |
|
|
|
||||||
|
2h |
|
|
a |
|
x |
|
|
|
arcsin |
|
|
|
|
|
2h |
|
|
a2h. |
||||||
|
|
|
|
2 |
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
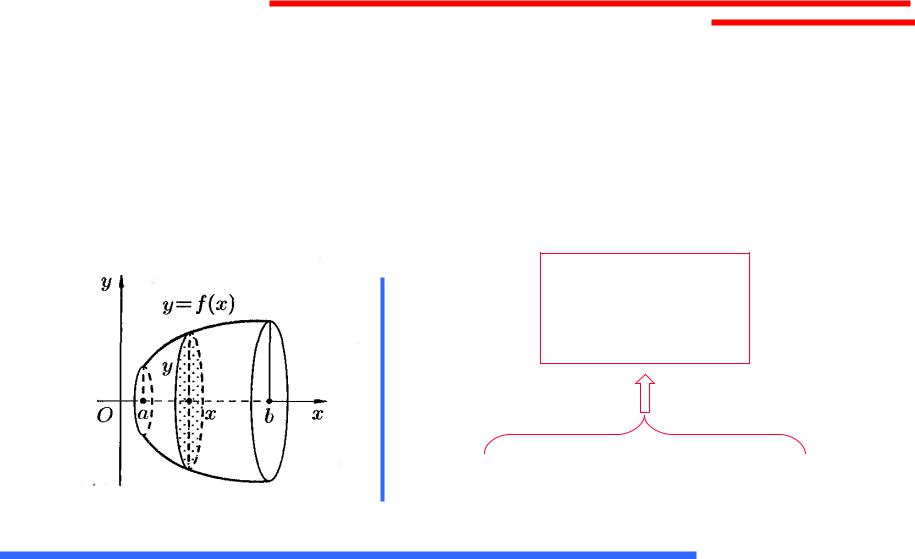
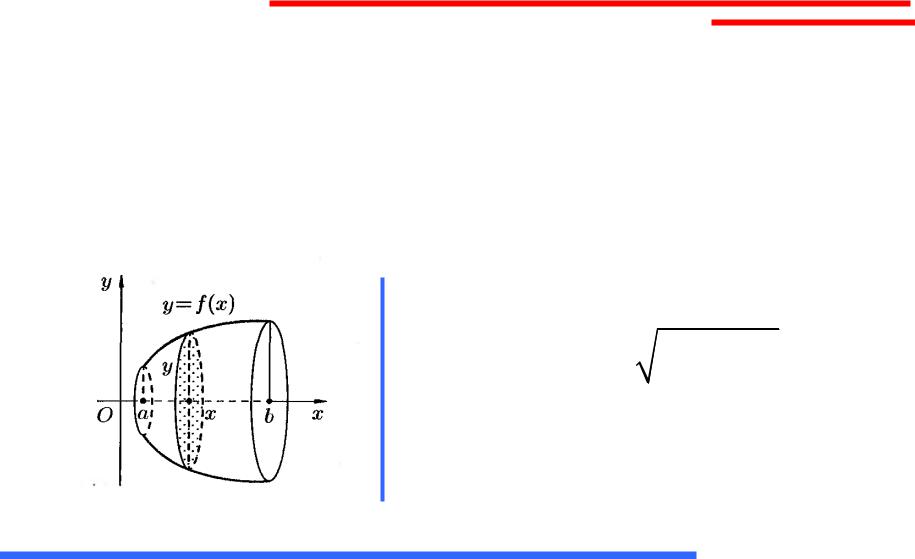
Объем тела вращения
Если криволинейная трапеция ограничена графиком непрерывной функции y f (x) 0
и прямыми y 0, x a, x b (a b), то объем тела, образованного вращением этой трапеции вокруг оси Ох, равен
h
Vx y2dx
a
b |
S(x) y2 |
V S(x)dx |
a
Объем тела вращения
Если криволинейная трапеция ограничена графиком непрерывной функции x ( y) 0
и прямыми x 0, y c, y d (c d ) , то объем тела, образованного вращением этой трапеции вокруг оси Оу, равен
d
Vy x2dy
c
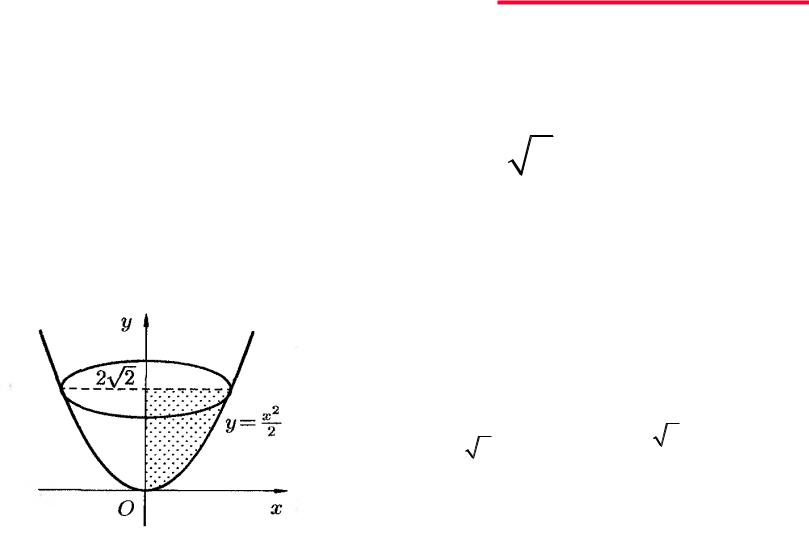
Пример:
Найти объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями
|
y |
x2 |
, x , 0, y 2 2 |
||
|
|
||||
, |
2 |
|
|
|
|
, |
|
Решение: |
|||
, |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
. |
|
|
|
Vy x2dy |
|
|
|
|
c |
|
|
|
|
|
|
|
|
Vy 2 |
|
2 2ydy y2 |
2 |
2 |
|
|
|
|
8 |
||
|
|
||||
|
0 |
|
|
0 |
|
|
|
|
|
||
.
Объем тела вращения
Если криволинейный сектор, ограниченный кривой
r r( ) |
и лучами , |
вращается вокруг полярной оси, то объем тела вращения равен
V2 r3 sin d
3
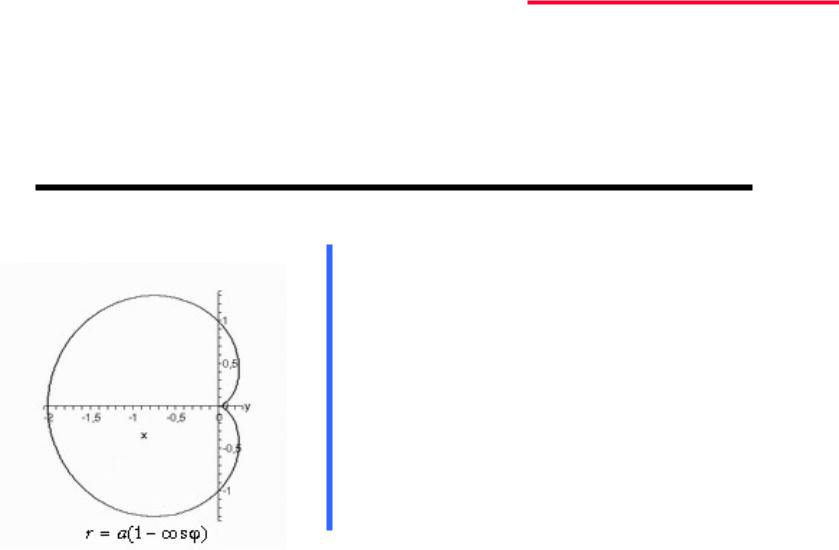
Пример:
Кардиоида r a(1 cos ) вращается вокруг полярной оси.
Найти, объем тела вращения
,
,
,
.
Решение: |
|
|
|
|
V |
2 |
|
||
|
||||
|
3 |
r3 sin d |
||
|
|
|
V2 a3(1 cos )3 sin d 3 0
2 |
a |
3 |
(1 cos )4 |
|
|
|
8 |
a |
3 |
|
|||||||||
3 |
|
4 |
|
|
3 |
|
|||
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
Площадь поверхности вращения
Если криволинейная трапеция ограничена графиком непрерывной функции y f (x) 0
и прямыми y 0, x a, x b (a b), то площадь поверхности вращения, образованного вращением этой трапеции вокруг оси Ох, равна
b |
( yx )2 dx |
Sx 2 y 1 |
|
a |
|