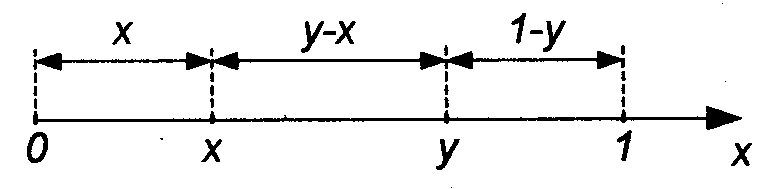4. Свойства вероятности.

Вероятность события обладает следующими свойствами.

1⁰. Для любого события справедливо неравенство .

2⁰. Вероятность невозможного события равна нулю, а вероятность достоверного события – единице.

Свойства 1⁰ и 2⁰ следуют непосредственно из определения вероятности.

3⁰. Для любых событий и

. (4.1)

4⁰. Если события и несовместны, т.е. , то

5⁰. Для вероятности противоположного события справедливо равенство

. (4.3)

6⁰. Для произвольных событий и имеет место равенство

. (4.4)

Методом математической индукции можно доказать общую формулу для вероятности суммы произвольных событий:

, (4.4)’

где суммы распространяются на различные значения индексов ; ; , и т. д.

Формула (4.4)’ выражает вероятность суммы произвольных событий через вероятности произведения этих событий, взятых по одному, по два, по три и т. д.

7⁰. Если , то для любых событий и

. (4.5)

8⁰. Пусть – произвольные события. Тогда

, (4.6)

где – событие, противоположное .

Приведём решения задач, иллюстрирующие свойства 1⁰ – 8⁰.

Пример 4.1. В урне 20 шаров: 10 красных, 7 синих и 3 белых. Найти вероятность того, что извлечённый наугад шар – цветной.

D Пусть – событие, заключающееся в извлечении красного шара, – синего. Так как эти события несовместны и , а , то по формуле (4.2) искомая вероятность (красный или синий шар) . ▲

Пример 4.2. Вероятность того, что будет снег (событие ), равна 0,7, а того, что будет дождь (событие ), – 0,35. Определить вероятность плохой погоды, если вероятность дождя со снегом (событие ) равна 0,15.

D События и совместны. Тогда, согласно формуле (4.4), вероятность (дождь или снег)

. ▲

Часто удобнее найти вероятность события с помощью вероятности противоположного события по формуле (4.3).

Пример 4.3. В ящике имеется деталей, среди которых стандартных. Найти вероятность того, что среди наугад извлечённых деталей имеется хотя бы одна стандартная.

D Пусть – событие, состоящее в том, что среди извлечённых деталей имеется хотя бы одна стандартная. Тогда означает, что среди извлечённых деталей нет ни одной стандартной. Найдём . Число способов извлечения деталей из равно , а число способов извлечения нестандартных деталей из нестандартных деталей – . Тогда и по формуле (4.3) искомая вероятность

. ▲

5. Геометрическая вероятность.

Если пространство содержит бесконечное множество элементарных событий, формула (3.3) неприменима. Для вычисления вероятности появления события в том случае, когда результат опыта определяется случайным положением точек в некоторой области, используется определение геометрической вероятности. При этом любые положения точек в этой области считаются равновероятными. Назовём мерой области её длину, площадь, объём в одно-, двух- и трёхмерном случае соответственно. Обозначим меру области , а меру её части – . Пусть – событие, состоящее в попадании точки в указанную часть области. Тогда искомая вероятность события (геометрическая вероятность) определяется равенством

. (5.1)

Пример 5.1. На отрезок единичной длины бросают наудачу две точки. Они разбивают отрезок на три части. Какова вероятность того, что из этих отрезков можно построить треугольник (событие )?

D Заданный отрезок рассматриваем как отрезок числовой прямой. Координаты брошенных точек обозначим через и ; это числа из отрезка . Числа и можно рассматривать как координаты точки на плоскости (рис. 5.1). Так как , , то точки наудачу брошены в квадрат со стороной . Чтобы из трёх отрезков можно было построить треугольник, необходимо и достаточно выполнение неравенства треугольника для длин его сторон: каждая сторона треугольника меньше суммы двух других его сторон. При (рис. 5.2) получаем неравенства

, , ,

откуда после преобразования имеем систему неравенств

, , , .

Эта система неравенств определяет на плоскости треугольник (рис. 5.3, верхний треугольник). При (рис. 5.4) получаем систему неравенств

, , , ,

которая определяет на плоскости второй (нижний) треугольник (рис. 5.3). Поскольку (площадь единичного квадрата), (площадь двух треугольников, заштрихованных на рис. 5.3), то вероятность получить треугольник из указанных отрезков . ▲

Рис. 5.1

Рис. 5.2

Рис. 5.3

Рис. 5.4

Пример 5.2 (задача о встрече). Два студента договорились встретиться в некоторый промежуток времени , причём каждый из них приходит к месту встречи случайным образом и ждёт другого не более минут. Найти вероятность встречи студентов (событие ).

Рис. 5.5

D Пусть и – моменты прихода студентов к месту встречи. Областью равновозможных значений и является квадрат площадью (рис. 5.5). Встреча произойдёт, если . Этому неравенству удовлетворяют точки области, заключённой между прямыми и . Её площадь . Тогда искомая вероятность

. ▲