4. Гипотеза о значении математического ожидания нормально распределённой генеральной совокупности при неизвестной дисперсии.

Предположения те же, что и в предыдущем пункте, но только неизвестно. В этом случае в качестве статистики используют случайную величину

, (4.1)

которая, если верна гипотеза , имеет -распределение Стьюдента с числом степеней свободы , где – объём выборки.

Если альтернативная гипотеза имеет вид , то используем левостороннюю критическую область, которая удовлетворяет следующему условию:

. (4.2)

Если альтернативная гипотеза имеет вид , то используем правостороннюю критическую область:

. (4.3)

И, наконец, при альтернативной гипотезе используем двустороннюю критическую область:

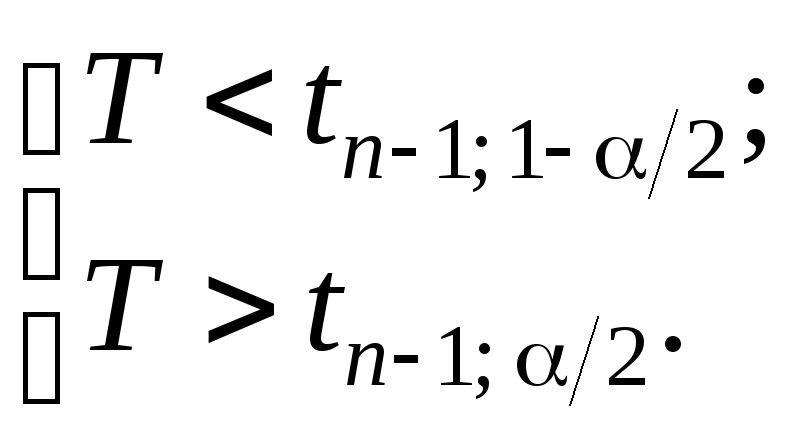(4. 4)

Перед вычислением по формуле (4.1) значения статистики нужно по выборке вычислить и .

Пример 4.1. По выборке объёма , извлечённой из нормальной генеральной совокупности, найдены выборочное среднее и исправленное выборочное среднее квадратическое отклонение . Требуется при уровне значимости проверить нулевую гипотезу при альтернативной гипотезе .

Δ Найдём значение статистики по формуле (4.1)

.

По условию альтернативная гипотеза имеет вид , поэтому критическая область – двусторонняя.

По таблице критических точек распределения Стьюдента (см. таблицу 5), по уровню значимости и по числу степеней свободы находим критическую точку .

Поскольку значение статистики , т.е. не попадает в критическую область, то гипотезу нет оснований отвергнуть. Другими словами, выборочное среднее незначительно отличается от гипотетического генерального среднего . ▲

5. Гипотеза о дисперсии нормально распределённой генеральной совокупности.

Предполагаем, что генеральная совокупность имеет нормальное распределение , где параметр неизвестен. Требуется при уровне значимости проверить гипотезу . В качестве статистики используем случайную величину

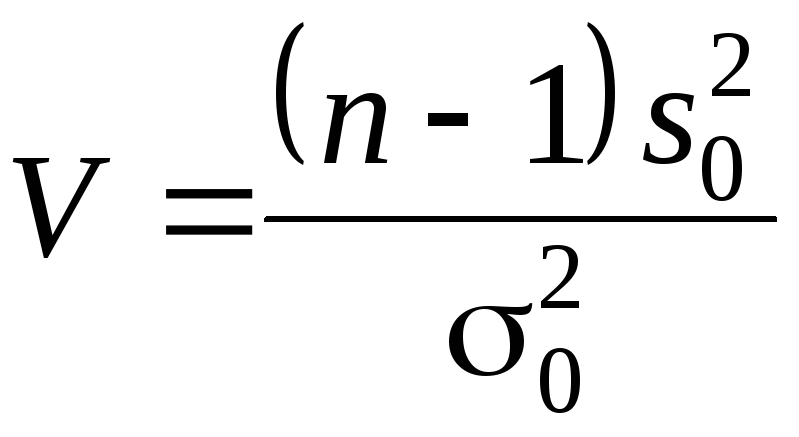. (5.1)

Если гипотеза верна, то случайная величина имеет -распределение Пирсона с числом степеней свободы , где – объём выборки.

Критическая область определяется в зависимости от альтернативной гипотезы по таблице -распределения (таблица 4).

Если альтернативная гипотеза имеет вид , находим левостороннюю критическую область исходя из условия

. (5.2)

При альтернативной гипотезе находим правостороннюю критическую область исходя из условия

. (5.3)

При альтернативной гипотезе находим двустороннюю критическую область согласно условию

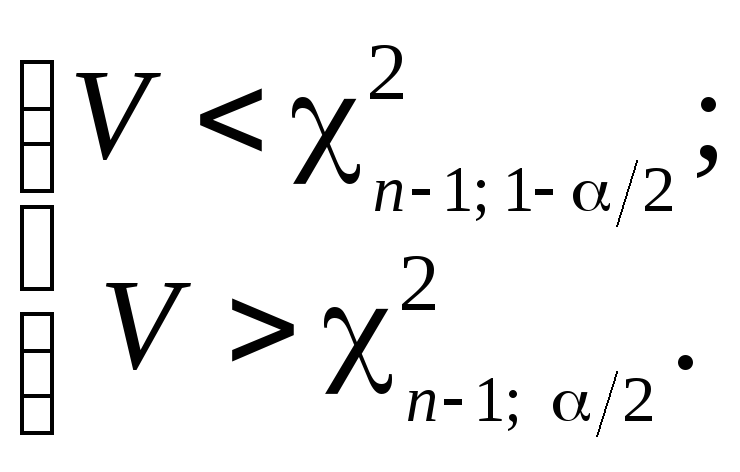. (5.4)

Перед вычислением по формуле (5.1) значения статистики нужно вычислить по выборке .

Замечание. Если число степеней свободы , то критическую точку можно найти из равенства Уилсона – Гильферти:

, (5.5)

где находят, используя функцию Лапласа (см. таблицу 3), из равенства (3.6).

Пример 5.1. Из нормально распределённой генеральной совокупности извлечена выборка объёма и по ней найдена исправленная выборочная дисперсия . Требуется при уровне значимости проверить нулевую гипотезу , приняв в качестве альтернативной гипотезы .

Δ Найдём значение статистики по формуле (5.1):

.

По условию, альтернативная гипотеза имеет вид , поэтому критическая область – правосторонняя. По таблице 4, по уровню значимости и числу степеней свободы находим критическую точку .

Так как , т.е. не попадает в критическую область, то гипотезу нет оснований отвергнуть. Другими словами, различие между исправленной дисперсией и гипотетической генеральной дисперсией незначимо. ▲

Пример 5.2. Партия изделий принимается, если дисперсия контролируемого размера значимо не превышает 0,2. Исправленная выборочная дисперсия, найденная по выборке объёма , оказалась равной . Можно ли принять партию при уровне значимости ?

Δ Нулевая гипотеза . Альтернативная гипотеза .

Найдём значение статистики по формуле (5.1):

.

Альтернативная гипотеза имеет вид , следовательно, критическая область правосторонняя. Поскольку в таблице 4 не содержится числа степеней свободы , найдём критическую точку приближённо из равенства Уилсона – Гильферти (5.5).

Найдём предварительно (учитывая, что по условию ) из равенства (3.6)

.

По таблице функции Лапласа (см. таблицу 3), используя линейную интерполяцию, находим: . Подставив , в формулу Уилсона – Гильферти, получим . (Это приближение достаточно хорошее: в более полных таблицах приведено значение 158,95).

Так как значение статистики , т.е. попадает в критическую область, нулевую гипотезу отвергаем. Партию принять нельзя. ▲

6. Критерий согласия (критерий Пирсона).

Критерий согласия – это критерий, с помощью которого проверяют гипотезу о том, что генеральная совокупность имеет распределение предполагаемого типа.

Имеется несколько критериев согласия: хи-квадрат, Колмогорова – Смирнова, и др.

Критерий является универсальным. Он применим для проверки любого вида распределения. Критерий позволяет выполнить проверку гипотезы о соответствии опытного закона распределения предполагаемому не только в случаях, когда последний известен полностью, но и тогда, когда параметры предполагаемого закона распределения определяются на основании опытных данных.

Пусть – выборка объёма наблюдений случайной величины . Проверяется гипотеза утверждающая, что имеет функцию распределения .

Проверка гипотезы при помощи критерия осуществляется по следующей схеме.

1) По выборке наблюдений находят оценки неизвестных параметров предполагаемого закона распределения случайной величины .

2) Область возможных значений случайной величины разбивается на интервалов в случае, когда – непрерывная с.в., или групп, состоящих из отдельных значений, для дискретной с.в. .

3) Исходя из предполагаемого закона распределения с.в. , находят теоретическую вероятность того, что значение принадлежит интервалу , т.е. , , при этом , , где – число элементов выборки, принадлежащих интервалу (эмпирическая частота попадания в -й интервал).

4) Вычисляют выборочное значение статистики критерия по формуле

. (6.1)

Близость частот к вероятности свидетельствует в пользу основной гипотезы , заметные различия отвергают гипотезу .

5) Определяют число степеней свободы распределения по формуле

,

где – число параметров предполагаемого закона распределения, найденных опытным путем.

6) Зная число степеней свободы и уровень значимости критерия, по таблицам определяют критическое значение :

.

7) Гипотеза согласуется с результатами наблюдений на уровне значимости , если

.

Если же , то гипотеза о виде функции распределения отклоняется, т.е. используем только правостороннюю критическую область.

Замечание. Критерий использует тот факт, что случайная величина , , имеет распределение, близкое к нормальному . Чтобы это утверждение было достаточно точным, необходимо, чтобы для всех интервалов выполнялось условие , т.е. в каждом интервале должно быть не менее 5 значений величины . Если в некоторых интервалах условие не выполняется, то их следует объединить с соседними.

Пример 6.1. В результате испытания 200 элементов на длительность работы получено эмпирическое распределение, приведённое в таблице 6.1 (в первом столбце указаны интервалы времени в часах, во втором столбце – частоты, т.е. количество элементов, проработавших время в пределах соответствующего интервала).

Таблица 6.1

Границы интервала	Частота наблюдения	Границы интервала	Частота наблюдения
0 – 5	133	15 – 20	4
5 – 10	45	20 – 25	2
10 – 15	15	25 – 30	1

Требуется, при уровне значимости , проверить гипотезу о том, что время работы элементов распределено по показательному закону.

Δ 1) – 2) Найдём среднее время работы всех элементов (в качестве среднего времени работы одного элемента примем середину интервала, которому принадлежит элемент):

.

Найдём оценку параметра предполагаемого показательного распределения:

.

Таким образом, функция плотности вероятности предполагаемого показательного распределения имеет вид

.

3) Найдём теоретические вероятности попадания случайной величины в каждый из интервалов по формуле

.

Например, для первого интервала

.

Аналогично вычислим вероятности попадания в остальные интервалы:

; ; ; ; .

Найдём теоретические частоты:

,

где – вероятность попадания в -й интервал.

Например, для первого интервала

.

Аналогично вычислим остальные теоретические частоты:

; ; ; ; .

4) Сравним эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого составим расчётную таблицу 6.2, причём объединим малочисленные частоты (4+2+1=7) и соответствующие им теоретические частоты (6,30+2,32+0,84=9,46).

Таблица 6.2

1	133	126,42	6,58	43,2964	0,3425
2	45	46,52	–1,52	2,3104	0,0497
3	15	17,10	–2,10	4,4100	0,2579
4	7	9,46	–2,46	6,0516	0,6397
	200

5) – 6) По таблице критических точек распределения (таблица 4), уровню значимости и числу степеней свободы ( – число интервалов, – число параметров показательного распределения) находим критическую точку правосторонней критической области

.

7) Так как , то гипотезу о распределении случайной величины по показательному закону нет оснований отвергнуть. Другими словами, данные наблюдений согласуются с этой гипотезой. ▲

12

© Гуров Владимир Владимирович, 2012