Цель работы: изучение гармонических колебаний; определение приведенной длины физического маятника и ускорения свободного падения.

Основные понятия

Простейшим типом колебаний является гармоническое колебание, ко­гда смещение тела от положения равновесия зависит от времени по закону синуса или косинуса (рис. 1 а):

(1)

где Х - величина смещения тела от положения равновесия, А - амплиту­да колебания - максимальное смещение от положения равновесия; ампли­туда равна максимальному абсолютному значению x в моменты t, когда

функция sin или cos принимает значения ±1, t+₀ - фаза колебания, оп­ределяющая положение колеблющегося тела в данный момент.

Основные характеристики колебаний - амплитуда, частота, период. Частота колебаний равна числу полных колебаний, совершаемых за едини­цу времени. Единицей частоты является Герц (Гц) - частота такого колеба­ния, при котором за 1с совершается одно полное колебание. Периодом ко­лебаний называется промежуток времени, за который совершается одно полное колебание. Период связан с частотой соотношением: Tv= l.

Циклическая или круговая частота колебания численно равна числу

полных колебаний, совершаемых за 2 секунд:  = 2.

Тело совершает гармонические колебания, когда на него действует упругая сила, пропорциональная величине смещения от положения равно­весия

(2)

где k - коэффициент упругости. Знак минус указывает, что возвращающая сила направлена в сторону, противоположную смещению, то есть к поло­жению равновесия.

Запишем для колеблющегося тела второй закон Ньютона:

(3)

Уравнение можно переписать и ввести обозначение:

(4)

Тогда уравнение примет вид:

(5)

Это и есть дифференциальное уравнение гармонических колебаний. Одним из решений такого уравнения является . Цикли­ческая частота колебания ₀ называется циклической частотой собствен­ных колебаний. Период таких колебаний:

(6)

При гармоническом колебательном движении кинетическая энергия колеблющейся материальной точки непрерывно меняется. Меняется и по­тенциальная энергия взаимодействия между точкой и окружающими тела­ми.

Кинетическая энергия колеблющейся точки массой m:

Потенциальная энергия квазиупругих сил, отсчитываемая от положе­ния равновесия данной материальной точки:

,

где x - смешение колеблющейся точки от положения равновесия, k - ко­эффициент квазиупругой силы.

Полная энергия материальной точки, совершающей гармоническое

колебание с частотой  и амплитудой А:

В процессе движения происходит непрерывный переход кинетической энергии в потенциальную и обратно, но полная энергия - величина посто­янная, она пропорциональна квадрату амплитуды колебаний.

Собственные гармонические колебания системы - это идеальный слу­чай колебаний, когда энергия системой не теряется и амплитуда остается постоянной. В случае реальных колебаний энергия, переданная системе, постепенно расходуется на преодоление сил сопротивления, поэтому ам­плитуда колебаний уменьшается, колебания затухают. Эти колебания на­зываются затухающими (рис. 1 б, в). Их частота определяется свойствами колеблющейся системы - массой, возвращающей силой, сопротивлением.

Если сила сопротивления среды пропорциональна скорости колебания, то есть, второй закон Ньютона для колеблющейся точки запишется:

(7)

Введем обозначения 2β = r/m ; ω₀²=k/m.

Решение уравнения (7) имеет вид:

(8)

Амплитуда затухающих колебаний, уменьшается по закону (рис. 1б), частота затухающих колебаний

, (9)

Если ω₀<β , частота является мнимым числом и имеет место апе­риодический процесс - рис. 1в

Рис 1.

В случае затухающих колебаний энергия убывает по закону

(10)

Величина отношения энергии к мощности потерь за время Т/2π = 1/ω характеризует способность колебательной системы сохранять энергию и называется добротностью:

(11)

Добротность равна числу колебаний за время, за которое амплитуда уменьшается в e^π раз, а энергия в е ^2π раз.

Степень затухания колебаний характеризуется логарифмическим дек­рементом, который определяет затухание колебаний за период:

(12)

Для изучения колебаний можно использовать физический или матема­тический маятники.

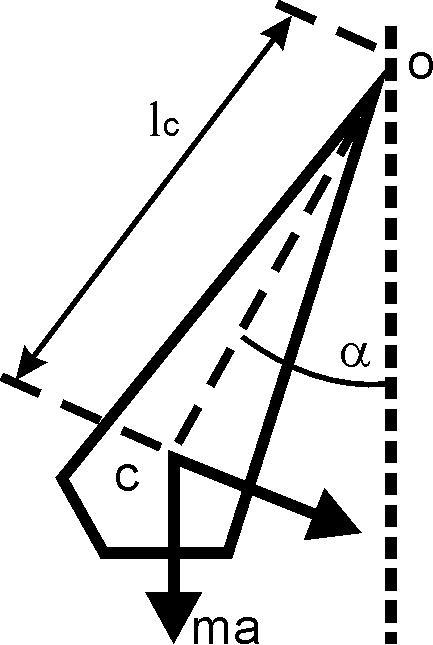
Каждое тело, подвешенное в точке, лежащей выше его центра тяже­сти, может колебаться и представляет собой физический маятник. На рис. 2 изображен физический маятник, отклоненный от положения равновесия.

Через точку О перпендикулярно рисунку проходит неподвижная ось, вокруг которой совершаются колеба­ния, С - центр тяжести маятника (точка, в которой приложена сила тя­жести mg).

Момент силы mg относительно оси О равен , где 1C - расстояние от оси вращения до центра тяжести - точки С. При малых углах отклонения, когда можно при­нять , основной закон ди­намики вращательного движения, опи­сывающий колебания такого маятника, можно записать в виде: (13) где J - момент инерции физического маятника относительно оси вращения. Это уравнение аналогично дифференциальному уравнению (5); величина является квадратом круговой частоты гармонических колебаний:

Рис. 2

(14)

Решение уравнения (13) описывает гармо­нические колебания, совершаемые физическим маятником. Период таких колебаний:

(15)

Для математического маятника (математическим маятником называют колеблющееся тело, размерами которого можно пренебречь по сравнению с расстоянием от центра масс тела до оси вращения) в случае малых углов отклонения дифференциальное уравнение колебаний выглядит:

(16)

Период колебаний математического маятника:

(17)

Физический маятник, описываемый (13), колеблется так же (с таким же периодом), как и математический маятник, описываемый (16), имею­щий длину где lс - расстояние от О до С.

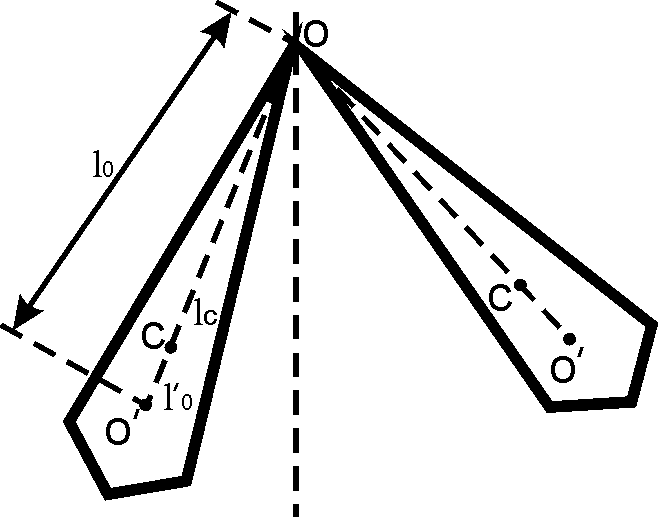
Приведенной длиной 1о физического маятника называется длина та­кого математического маятника, который имеет тот же период колебаний, что и данный физический маятник.

Если к оси физического маятника подвесить груз на нити такой длины, чтобы она была равна приведенной длине данного физического ма­ятника (рис. 3), то отклоненные на одинаковый угол физический маятник и

Рис. 2

груз колеблются вместе, так что груз все время находится в одной и той же точке физическо­го маятника - его центре качаний. Приведенная длина 1о все­гда больше 1с , то есть центр ка­чаний всегда лежит ниже центра тяжести. По теореме Штейнера момент инерции относительно оси маятника, где J0 - момент инерции относи­тельно оси, проходящей через центр тяжести. Поэтому приведенная длина будет Точка подвеса и центр качаний обратимы. Теорема Гюйгенса: если физический маятник подвесить за центр качания, его период не изменится и прежняя точка подвеса будет новым центром качания. Докажем теорему Гюйгенса следующим образом. Расстояние СО' от

центра тяжести до но­вой оси О' , где 1о ⁼⁼ 00' - прежняя приведенная длина, 1с ⁼ ОС - расстояние от центра тяжести до прежней оси. Поэтому новая приведенная длина будет равна:

(18)

где J’ - момент инерции маятника относительно оcи О'.

По теореме Штейнера J' = Jo + m(lo - 1с)², откуда

(19)

где Jo - момент относительно оси, проходящей через центр тяжести . Но, с другой стороны, так как , подставив в (19), получим:

(20)

Мы получили, что l₀’=l₀ –обратимость точки подвеса и центра качаний.