
01_03 Лекции ФМП
.pdf
|
|
u |
u |
|
u |
|
2 |
0 |
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
xx |
xy |
|
xz |
|
|
|
|
|
|
|
|
|
|
||
|
|
u |
u |
|
u |
|
0 |
2 |
0 |
. |
|
|
|
|
|||
|
|
yx |
yy |
|
yz |
|
|
|
|
|
|
|
|
|
|
||
|
|
u |
u |
|
u |
|
0 |
0 |
2 |
|
|
|
|
|
|||
|
|
zx |
zy |
|
zz |
|
|
|
|
|
|
|
|
|
|
||
Отсюда следует, что при 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A 2 0 , |
A |
|
2 |
0 |
|
4 0 , A |
|
2 |
0 |
0 |
|
8 0 . |
|||||
|
|
|
|
||||||||||||||
|
|
||||||||||||||||
|
|
|
0 2 |
0 |
|
||||||||||||
1 |
2 |
|
|
0 |
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно, при 0 второй дифференциал (25) в точке M 0 |
представляет собой положитель- |
||||||||||||||||
но определенную квадратичную форму, и потому функция (24) имеет в точке M 0 (0, 1, 1) локаль-
ный минимум.
При 0 второй дифференциал (25) представляет собой знакопеременную квадратичную форму, так как, например, он положителен при dx 0 , dy 1, dz 1 и отрицателен при dx 1,
dy 0 , dz 0 . Таким образом, если 0 , то функция (24) не имеет локального экстремума в точке M 0 . ▲
Пример. Исследовать на экстремум функцию u x3 y3 3xy .
∆ Для нахождения экстремума данной функции воспользуемся следствием к рассмотренной теореме. Найдем вначале частные производные первого порядка и приравняем их нулю:
u |
3(x2 y) 0 , |
u |
3( y2 x) 0 . |
||
x |
|
y |
|
|
|
Эти равенства определяют систему уравнений |
x2 |
y 0, |
для нахождения стационарных |
||
|
|
||||
|
|
|
y 2 |
x 0 |
|
точек. Решая систему, |
найдем две стационарные точки M1 (0,0) и M 2 (1,1) . Найдем теперь произ- |
||||||||||||||||||||||||
водные второго порядка: |
2u |
6x , |
|
2u |
3 , |
2u |
6 y . Вычислим величину D для каждой ста- |
||||||||||||||||||
x2 |
|
x y |
y 2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ционарной точки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для точки M1 имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A |
2u |
|
0 |
, B |
|
|
2u |
|
3 |
, C |
2u |
|
|
0 , D 0 0 ( 3)2 9 0 . |
||||||||||
|
x2 |
|
|
|
x y |
y 2 |
|
|
|||||||||||||||||
|
|
|
|
M1 |
|
|
|
|
|
|
M1 |
|
|
|
|
|
M1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, экстремума в точке M1 нет. |
|
|
|
|
|
|
|
|
|
||||||||||||||||
Для точки M 2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A |
2u |
|
|
6 , |
B |
|
2u |
|
|
3 , |
C |
|
2u |
|
|
|
6 |
, |
D 6 6 ( 3)2 27 0 , A 6 0 . |
||||||
|
|
|
|
|
|
|
|||||||||||||||||||
x2 |
|
|
x y |
|
|
y2 |
|
|
|
||||||||||||||||
|
|
M 2 |
|
|
|
M 2 |
|
|
|
|
M 2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Следовательно, в точке M 2 функция имеет локальный минимум, равный umin u(M 2 ) u(1,1) 1 1 3 1. ▲
Условный экстремум и метод неопределенных множителей Лагранжа
В предыдущей теме нами рассмотрен вопрос отыскания локальных экстремумов функции, аргументы которой не связаны никакими дополнительными условиями, то есть являются независимыми переменными. Вместе с тем, в различных приложениях часто встречается задача об отыскании экстремумов функции, аргументы которой удовлетворяют дополнительным условиям связи. Экстремумы такого рода называют условными, чтобы отличить их от безусловных (или абсолютных) экстремумов, изученных ранее.
21

Приведем пример задачи о нахождении условного экстремума. Пусть требуется найти экстремумы функции u x2 y2 при условии, что переменные x и y этой функции удовлетворяют условию связи x y 1 0 . Это означает, что функция u x2 y2 рассматривается уже не на всей координатной плоскости xOy , а лишь на прямой x y 1 0 . Поэтому любое изменение x влечет за собой соответствующее изменение y , и наоборот – изменение y влечет определяемое соотношением x y 1 0 изменение x . Следовательно, исходная функция u является функцией только одной независимой переменной x (или y ).
Для решения поставленной задачи подставим в выражение функции u x2 y2 значение y , определяемое из условия связи x y 1 0 . Таким путем поставленная задача сводится к зада-
че об отыскании безусловного экстремума функции u 2x2 |
2x 1 одной независимой перемен- |
|
ной x . |
Так как u 4(x 1 2) , u 4 , то функция u 2x2 |
2x 1 имеет минимум u 1 2 при |
x 1 2 . |
Следовательно, функция u x2 y2 с условием x y 1 0 имеет условный минимум |
|
u 1 2 |
в точке (1 2,1 2) . Отметим, что безусловный минимум функции u x2 y2 достигается в |
|
точке (0,0) и равен u 0 .
Определение. Функция u f (M ) f (x1, x2 , , xn ) имеет условный максимум (условный ми-
нимум) в точке M 0 (x10 , x20 , , xm0 ) , если существует такая окрестность точки M 0 , что для всех точек M M 0 , удовлетворяющих уравнениям связи
k (M ) k (x1 , x2 , , xn ) 0 ( k 1, m , m n ),
выполняется неравенство f (M ) f (M 0 ) (соответственно f (M ) f (M 0 ) ).
Общий принцип нахождения условного экстремума заключается в следующем. Из уравнений связи выражаются одни переменные через другие, и после их подстановки в исходную функцию приходят к задаче на обычный (безусловный) экстремум, но уже для функции n m переменных. Данный метод использован в рассмотренном примере, однако, зачастую такой подход приводит к громоздким выкладкам, поэтому чаще используют другой метод – метод неопределенных множителей Лагранжа.
Рассмотрим метод неопределенных множителей Лагранжа для нахождения условного экстремума. Задача нахождения условного экстремума сводится к исследованию на обычный экстре-
мум функции Лагранжа
|
|
|
|
|
|
|
|
|
|
|
m |
|
||
|
|
L(x1 , x2 , , xn , 1 , 2 , , m ) f (x1 , x2 , , xn ) k k (x1 , x2 , , xn ) , |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
||
где числа k |
|
|
|
|
|
|
|
|
||||||
( k 1, m ) – называются множителями Лагранжа. |
|
|||||||||||||
|
Необходимые условия условного экстремума выражаются системой n m уравнений |
|
||||||||||||
|
|
|
|
L(M ) 0 , |
|
|
|
|
|
|
||||
|
|
|
|
i 1, n , |
k |
(M ) 0 , k 1, m , |
(26) |
|||||||
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из которой могут быть найдены неизвестные |
|
|
|
|
|
|
|
|||||||
|
|
|
|
x0 , x0 |
, , x0 |
, 0 , 0 |
, , 0 , |
|
||||||
|
|
1 |
2 |
|
n |
1 |
|
2 |
m |
|
||||
где x0 |
, x0 , , x0 – координаты точки, в которой возможен условный экстремум. |
|
||||||||||||
1 |
2 |
n |
|
|
|
|
|
|
|
|
|
|
||
|
Рассмотрим теперь достаточные условия условного экстремума функции нескольких пере- |
|||||||||||||
менных. Предположим, что в точке M 0 |
выполнены необходимые условия экстремума. Кроме то- |
|||||||||||||
го, дополнительно потребуем непрерывности всех частных производных второго порядка функций f и i , i 1, m в окрестности точки M 0 . Как было показано, для формулировки достаточного
условия экстремума в точке M 0 у функции f при наличии связей i , |
|
|
|
|
||||
i 1, m следует присоеди- |
||||||||
нить к необходимым условиям требование знакоопределенности d 2 L |
в этой точке. При этом |
|||||||
можно утверждать наличие в точке M |
0 |
минимума, если |
d 2 L |
0 , и максимума, если d 2 L |
0 . |
|||
|
|
|
M0 |
|
|
|
M0 |
|
|
|
22 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Пример. Найти условный экстремум функции u x 2y при x2 y2 |
5 . |
||
∆ Составим функцию Лагранжа |
|
|
|
L(x, y,) x 2y (x2 y2 5) . |
|
||
Отсюда |
|
|
|
L |
1 2x , |
L 2 2y . |
|
x |
|
y |
|
Система (26) состоит из трех уравнений
1 2x 0,2 2y 0,x2 y 2 5,
относительно трех неизвестных x , y , . Эта система имеет два решения:
|
|
|
|
|
|
x |
1, |
|
x |
|
1, |
|
|||
|
|
|
|
|
|
|
1 |
2, и |
|
|
|
2 |
2, |
|
|
|
|
|
|
|
|
y1 |
|
y2 |
|
||||||
|
|
|
|
|
|
|
|
1 2 , |
|
|
1 2. |
|
|||
|
|
|
|
|
|
|
1 |
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как |
2 L |
2 , |
2 L |
0 |
, |
2 L |
2 , то |
d 2 L 2 (dx2 dy2 ) , то есть d 2 L 0 |
|||||||
x2 |
x y |
y |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
и поэтому функция имеет условный минимум в точке M1 ( 1, 2) |
и umin 5 . |
||||||||||||||
При 1 2 оказывается |
d 2 L 0 . Следовательно, функция имеет условный |
||||||||||||||
точке M 2 (1,2) |
и umax 5 . ▲ |
|
|
|
|
|
|
|
|
|
|
|
|||
при 1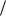 2 ,
2 ,
максимум в
Наибольшее и наименьшее значение функции в замкнутой области
Дифференцируемая функция в ограниченной замкнутой области D достигает своего наибольшего (наименьшего) значения либо в стационарной точке, лежащей внутри области D , либо на границе этой области. Покажем на примере способ нахождения наибольшего и наименьшего значения функции двух переменных в замкнутой ограниченной области.
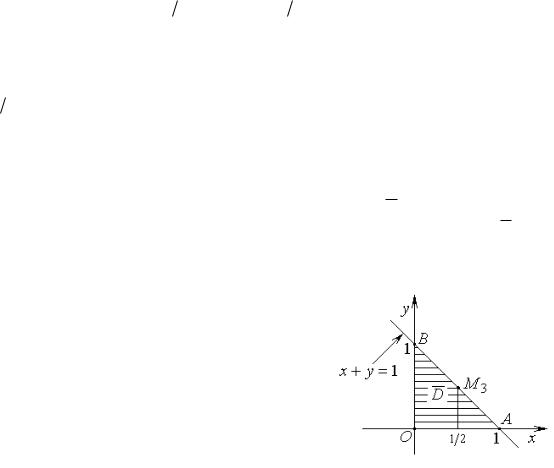
Пример. Найти наибольшее и наименьшее значение |
|
|
|||||||||||||
функции z xy y2 3x 4y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в замкнутой области D , ограни- |
|
|
|||||||||||||
ченной линиями x 0 , y 0 , |
x y 1 0 (рис. 3). |
|
|
||||||||||||
∆ Выясним сначала, существуют ли стационарные точ- |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
ки, лежащие внутри области |
|
D , то есть внутри треугольника |
|
|
|||||||||||
OAB . Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z y 3 0 , |
|
|
z x 2y 4 0 . |
|
|
||||||||||
x |
|
|
|
y |
|
|
|||||||||
Решая полученную систему уравнений, находим ста- |
|
|
|||||||||||||
ционарную точку M1 ( 10, 3) |
|
|
|
|
|
|
|
|
|
||||||
. Она лежит вне области D , сле- |
Рис. 3. |
||||||||||||||
довательно, при решении задачи ее не учитываем. Исследуем |
|||||||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||
значения функции на границе области D . |
|
|
|||||||||||||
На стороне OA ( y 0 , |
|
|
0 x 1) треугольника OAB функция z имеет вид |
z 3x . Стацио- |
|||||||||||
нарных точек на отрезке OA нет, так как z 3. В точках O(0,0) |
и A(1,0) соответственно z(O) 0 , |
||||||||||||||
z( A) 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На стороне OB ( x 0 , |
0 y 1) треугольника z y2 |
4y , z 2y 4 . |
Стационарную |
||||||||||||
точку находим из уравнения |
2y 4 0 . Отсюда y 2 . Полученная точка с |
координатами |
|||||||||||||
|
|
|
|
||||||||||||
M2 (0,2) не принадлежит области D , поэтому исключается ее из рассмотрения. |
В точке B(0,1) |
||||||||||||||
значение функции z равно z(B) 3. |
|
|
|||||||||||||
|
|
|
23 |
|
|
|
|
|
|
||||||

Находим наибольшее и наименьшее значения на стороне AB : x y 1 0 , 0 x 1. Здесь
y 1 x , z 2x2 |
2x 3 , тогда z 4x 2 и из |
z 0 следует x 1 2 , то есть стационарная точ- |
||||||
|
|
|
Значение функции в ней z(M3 ) 3,5 . Сравнивая |
|||||
ка M3 (1 2,1 2) принадлежит границе области D . |
||||||||
все |
полученные |
значения функции: z(O) 0 , |
z( A) 3, |
z(B) 3, |
z(M3 ) 3,5 , видим, что |
|||
zíàèá |
z(M3 ) z(1 |
2,1 2) 3,5 , |
zíàèì z(O) z(0,0) 0 . ▲ |
|
|
|||
24
