Секущая и нормаль к кривой линии

Прямая, пересекающая кривую линию в одной, двух и более точках, называется секущей (прямая m). Нормалью к кривой l называется прямая n, перпендикулярная к l и проходящая через точку касания А

Касательная к кривой линии

Касательной к кривой линии называется прямая, представляющая собой предельное положение секущей. Различают несколько типов касательных к кривой:

1. Касательная, параллельная заданному направлению

2. Касательная из заданной точки, не принадлежащей этой кривой

3. Касательная в точке кривой

Свойства точек кривой

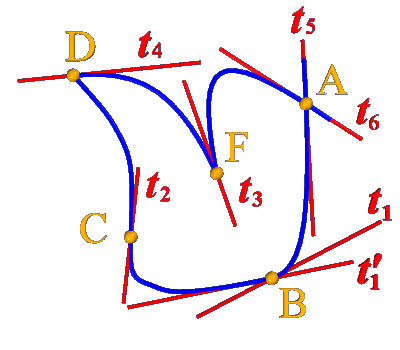
Особые точки кривой

Точка излома В – кривая в этой точке имеет две полукасательные.

Точка перегиба С – касательная пересекает кривую.

Точка возврата первого рода F (точка заострения) – полукасательные совпадают.

Точка возврата второго рода D (вершина клюва) – полукасательные совпадают.

Узловая точка – точка A, в которой кривая пересекает сама себя и имеет две касательные.

Кривизна кривой

При исследовании свойств кривой бывает необходимо  знать кривизну в ее отдельных точках. Направление кривой меняется от точки к точке. Чем более резко меняется направление кривой, тем больше ее кривизна.

Кривизна прямой линии во всех ее точках равна нулю, а кривизна окружности во всех точках постоянна.

Кривизна кривой в заданной точке определяется с помощью окружности, соприкасающейся с ней в этой точке.

Соприкасающейся окружностью называется предельное положение окружности, когда она проходит через данную точку и две другие бесконечно близкие к ней точки.

Центр и радиус соприкасающейся окружности определяют центр и радиус кривизны исследуемой кривой в данной точке.

Кривизной плоской кривой в данной точке называется величина, обратная радиусу соприкасающейся окружности.

В рассматриваемой точке кривая и соприкасающаяся с ней окружность имеют общие касательную и нормаль.

Построение центра и радиуса Кривизны

Определение центра и радиуса кривизны кривой m в заданной точке А выполняется в следующей последовательности:

1. На кривой по обе стороны от заданной точки отмечаем несколько точек.

2. Проводим из всех отмеченных точек полукасательные.

3. На полукасательных откладываем произвольные, но равные отрезки и через полученные точки проводим кривую.

4. Точке А заданной кривой соответствует точка A' построенной кривой. Проводим нормали к кривым в точках A и A'.

5. Точка пересечения нормалей 0 – центр кривизны кривой в точке А, а R_A − радиус кривизны кривой в этой точке.

Множество центров кривизны кривой – это линия, которую называют эволютой данной кривой. Кривая по отношению к своей эволюте называется эвольвентой.

Свойства ортогональных проекций кривой

1. Проекцией кривой линии является кривая линия.

2. Касательная к кривой линии проецируется в касательную к ее проекции.

3. Несобственная точка кривой проецируется в несобственную точку ее проекции.

4. Порядок линии – проекции алгебраической кривой равен порядку самой кривой или меньше.

5. Число узловых точек (в которых кривая пересекает сама себя) проекции равно числу узловых точек самой кривой.

Случаи, когда плоская кривая проецируется в прямую (свойства 1, 4, 5), а касательная – в точку (свойство 2), не учитываются.

Рассмотрим три случая расположения окружности относительно плоскостей проекции.

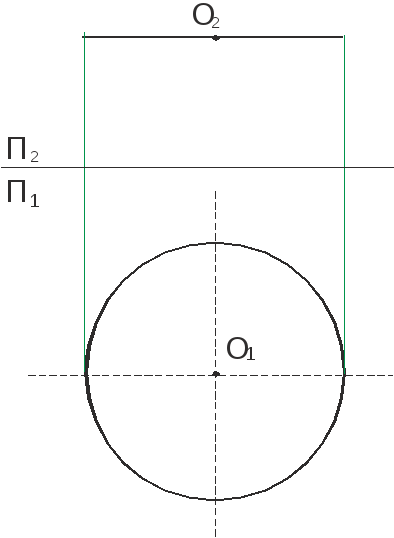
Случай 1. 

Окружность m лежит в плоскости  || П1. Проекция окружности  на П2 – отрезок, причем отрезок  параллелен оси П2 / П1.

На плоскость П1 окружность  проецируется в натуральную величину

Случай 2.

 Окружность  лежит в плоскости  П2 и под углом к плоскости П1. Проекция окружности  на П2 – отрезок. Проекция окружности на П1 – эллипс. Для уточнения формы эллипса используем вспомогательные точки и дугу радиусом данной окружности.

Случай 3. 

Окружность  лежит в плоскости общего положения. Обе проекции окружности  –эллипсы.