Пространственные кривые линии

Пространственные кривые линии в начертательной геометрии обычно рассматриваются как результат пересечения поверхностей или траектория движения точки.

Пространственную, так же как и плоскую, кривую линию на чертеже задают последовательным рядом точек.

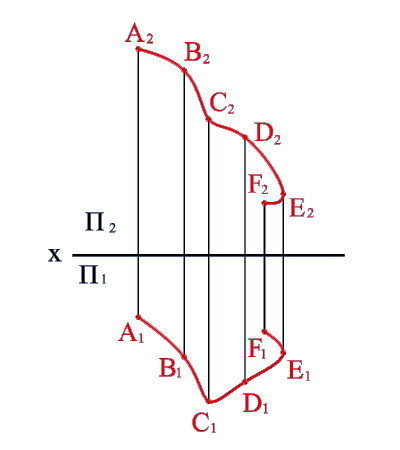
 Классическим примером пространственных кривых линий являются цилиндрическая и коническая винтовые линии

Цилиндрическая винтовая линия

Такую линию в пространстве описывает точка, которая движется по какой-либо образующей прямого кругового цилиндра, вращающегося вокруг своей оси так, что путь, проходимый точкой по образующей, пропорционален углу поворота цилиндра

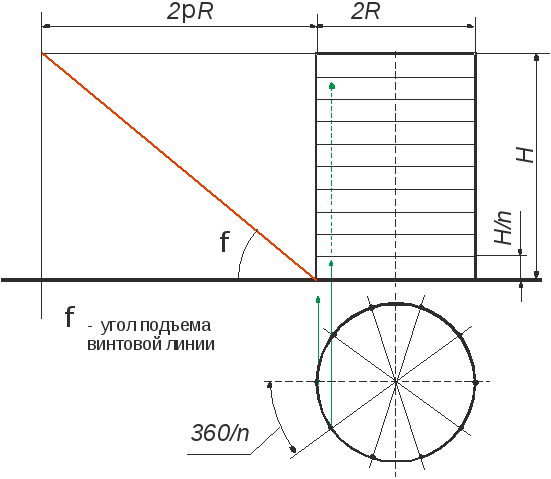
Смещение точки вдоль образующей за один оборот называется шагом цилиндрической винтовой линии. Различают правую и левую винтовые линии.

Горизонтальная проекция винтовой линии является окружностью, а фронтальная - синусоидой. На развертке цилиндрической поверхности винтовая линия изобразится в виде прямой. На рис.4 показан процесс формообразования винтовой линии.

Угол называется углом подъема винтовой линии. Этот угол равен углу наклона касательной t в любой точке винтовой линии к плоскости, перпендикулярной ее оси. Цилиндрическая винтовая пиния, подобно прямой и окружности, обладает свойством сдвигаемости.

Свойство сдвигаемости состоит в том, что каждый отрезок линии может сдвигаться вдоль нее, не подвергаясь деформации. Это свойство винтовой линии лежит в основе работы винтовых пар (винт-гайка). Винтовая линия является геодезической на цилиндрической поверхности.

Геодезической называется линия, принадлежащая поверхности и кратчайшая из всех линий, которые можно провести между двумя точками поверхности. Кроме цилиндрической винтовой линии, геодезическими линиями также являются прямая на плоскости, окружность большого круга на сфере и др.

Геодезическая линия изображается на развертке поверхности в виде прямой линии.

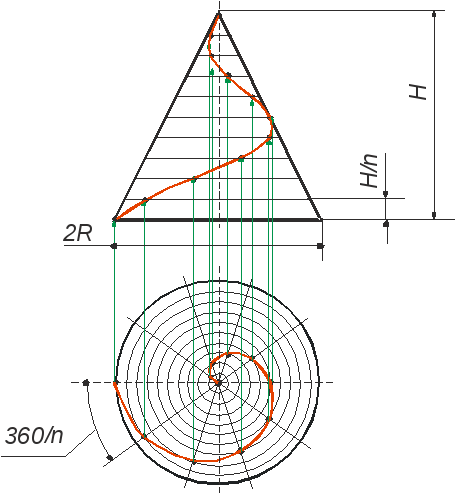
Коническая винтовая линия

Такую линию описывает точка, которая движется по какой-либо образующей прямого кругового конуса, вращающегося вокруг своей оси так, что путь, пройденный точкой по образующей, все время равен углу поворота конуса.

Кривые безье. Сплайны

В векторной графике кривые второго порядка используются для построения базовых форм (примитивов). Кривые второго порядка не имеют точек перегиба, кривые третьего порядка могут иметь одну точку прегиба.

В векторных редакторах применяют не любые кривые третьего порядка, а их особый вид, называемый кривыми Безье. Отрезки кривых Безье — это частный случай отрезков кривых третьего порядка. Они описываются не одиннадцатью параметрами, как произвольные отрезки кривых третьего порядка, а лишь восемью, и потому работать с ними удобнее.

Кривая Безье, названа в честь французского математика Пьера Безье (Р. Bezier), который применял математические кривые и поверхности в процессе конструирования кузова автомобиля Рено. Разработал пригодную к промышленному внедрению методику математического определения сложных кривых, которая позволила конструкторам манипулировать кривыми, ничего не зная о задающих их функциях. В результате этой самой работы и появились на свет кривые, которые теперь носят имя Безье

Кривые Безье – это частный вид кривых третьего порядка. В основе построения кривых Безье лежит использование двух касательных, проведенных к крайним точкам отрезка.

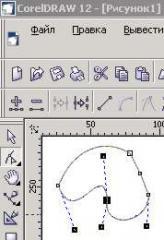
На практике эти касательные выполняют роль «рычагов», с помощью которых линию изгибают так, как это необходимо. На форму линии влияет не только угол наклона касательной, но и длина ее отрезка. Управление касательной (а вместе с ней и формой линии) производят перетаскиванием маркера с помощью мыши. Линия задается графически.

Появление кривых Безье вызвало настоящий переворот в видео и трехмерной графике. Это связано с тем, что до появлении формул Безье контуры компьютерных деталей были ломанными, а движения прерывистыми.

В компьютерной графике используется часто понятия сплайн для определения кривых.

В современных словарях можно найти более точное определение слова сплайн: «заданная математической функцией плавная кривая, соединяющая ряд точек.