4.Методика составления схем замещения, приемы приведения их к простейшему виду.

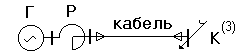Если исходная расчетная схема не содержит трансформаторы, то есть имеет одну ступень напряжения, то при составлении схемы замещения такая схема не нуждается в эквивалентировании, так как все ее элементы находятся на одной и той же ступени напряжения. Например, схема на рис.2.1.

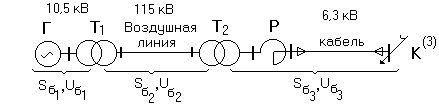Если же расчетная схема имеет вид, приведенный на рис.2.2., то такую схему нужно эквивалентировать, то есть параметры всех элементов схемы следует привести к одной (основной) ступени напряжения. Выбор основной ступени напряжения произволен, однако в ходе решения конкретной задачи он должен оставаться неизменным.

Для приведения схемы замещения к эквивалентному виду при расчете токов к.з. в относительных единицах следует выбрать значение базисной мощности , которая остается одной и той же для всех ступеней напряжения, то есть.

Базисные напряжения для каждой ступени напряжения будут иметь различные значения. Для определения базисных напряжений других ступеней напряжения при произвольно принятой ступени напряжения в качестве основной (базисной), следует исходить из общей теории трансформатора и определять их значения по формуле

, (2.16)

где - базисное напряжениеступени;- базисное напряжение ступени, принятую за основную базисную;-коэффициенты трансформации трансформаторов на пути от ступени, принятой за основную базисную, к ступени напряжения, базисное напряжение которой определяется.

На практике (при отсутствии действительных значений коэффициентов трансформации) нередко пользуются приближенным методом эквивалентирования, который часто обеспечивает приемлемые результаты. В этом случае за базисные напряжения ступеней принимают средние значения этих ступеней.

Способы приведения схем замещения к простейшему виду

Одним из условий расчета токов к.з. является необходимость приведения исходной схемы замещения к простейшему виду, то есть к получению значений результирующей э.д.с. Е_ и результирующего сопротивления Х_ для исходной схемы.

Так значения последовательно включенных сопротивлений суммируются, для параллельно включенных – суммируются их проводимости, а для смешанных схем соединений применяют оба способа. Сеть, состоящая из последовательных, параллельных и смешанных схем соединения сопротивлений является простой сетью, и она легко приводится к простейшему виду.

Если сеть содержит замкнутые контуры, то она является сложной, и для приведения ее к простейшему виду следует использовать другие приемы. Рассмотрим некоторые из них.

а)Замена нескольких генераторных ветвей, сходящихся в одной точке, одной эквивалентной.

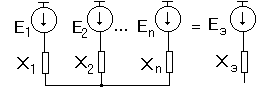Пусть имеется схема замещения (рис.2.4), содержащая генераторных ветвей, сходящихся в одной точке.

Рис.2.4.

эквивалентная э.д.с., то есть э.д.с. генератора, которая заменяет э.д.с . генераторов и эквивалентное сопротивление, могут быть определены по формулам:

; (2.17)

, (2.18)

где - проводимости генераторных ветвей.

б)Преобразование многолучевой звезды в соответствующий многоугольник

В этом случае (рис. 2.5, а), сохраняя опорные точки звезды , получают многоугольник (рис.2.5, б)

Рис.2.5.

Сопротивления сторон многоугольника определяют по формуле

(2.19)

где - сопротивление стороны многоугольника;

-сопротивления лучей звезды и;

-сумма проводимостей всех лучей звезды.

Далее, получив многоугольник, рассекают точку и получают схему (рис.2.6), дальнейшее преобразование которой не вызывает затруднений.

в)Преобразование трехлучевой звезды в треугольник и наоборот (рис.2.7)

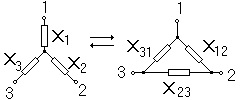
Рис.2.7.

В качестве примера приведем формулы для определения и

; (2.20)

. (2.21)

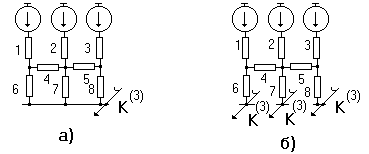
г) Металлическое трехфазное к.з. находится в узле с несколькими сходящимися в нем ветвями (рис.2.8, а).

В этом случае этот узел можно разрезать, сохранив на конце каждой образовавшейся ветви такое же к.з. Далее полученную схему нетрудно преобразовать относительно любой из точек к.з., учитывая другие ветви с к.з., как нагрузочные с э.д.с, равными нулю (рис.2.8, б).

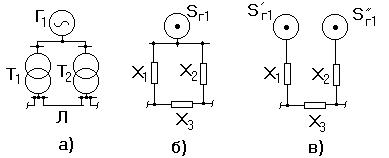
д)Разнесение мощностей или токов, подходящих к вершине треугольника сопротивлений (рис.2.11, а, б) по ветвям разомкнутого треугольника (рис.2.11, в)

При разнесении мощности расчетные соотношения имеют вид:

; ;. (2.22)

При расчете линейных электрических цепей часто удобно использовать принцип наложения. Согласно этому принципу действительный режим получают как результат наложения ряда условных режимов, каждый из которых определяется в предположении, что в схеме приложена одна (или группа) э.д.с., в то время как все остальные равны нулю; при этом все элементы схемы замещения остаются вк= ббббббббббббббблюченными.

При большом числе э.д.с. расчет токов к.з. при применении принципа наложения в такой форме становится громоздким и слишком неудобным.

В этой связи при рачете токов к.з. обычно используют следующие формы принципа наложения:

1)Наложение собственно аварийного режима на предшествующий

Дело в том, что условия металлического трехфазного к.з. не изменятся, если представить, что в точке к.з. приложены две равные, но взаимно противоположные э.д.с, величина которых может быт

ь произвольной. В частности, ее можно принять раной напряжению, которое было в этой точке до возникновения в ней к.з.

При таком подходе режим в схеме замещения после возникновения к.з. удобно представить состоящим из двух режимов.

Первый режим получают, учитывая все э.д.с. генераторов до возникновения к.з., и дополнительную э.д.с., введенную в точку к.з., равную (в данной точке).

Очевидно, то одновременное действие этих э.д.с. дает предшествующий режим в рассматриваемой схеме замещения.

Второй режим получают путем введения только одной э.д.с. в точке к.з., равной . Этот режим называют собственно аварийным, а получающиеся при нем токи и напряжения – аварийными составляющими токов и напряжений.

Суммируя токи и напряжения предшествующего режима с их аварийными составляющими, получают действительные величины токов и напряжений в схеме замещения при металлическом трехфазном к.з. в заданной точке, то есть

; . (2.23)

Здесь , так как.

2)Применение собственных и взаимных сопротивлений и проводимостей

В схеме с произвольным числом э.д.с. для тока, например, источника 1, считая положительным направлением тока путь от источника к внешней сети, по принципу наложения можно записать:

, (2.24)

где каждый из токов обусловлен действием лишь одной э.д.с. при равенстве нулю остальных, то есть - собственный ток источника 1, созданный только его э.д.с.;- взаимный ток ветви 1, вызванный действием только э.д.с.и т.д.

Здесь - соответственно, собственная и взаимные проводимости источника 1 в рассматриваемой схеме.

Аналогично для тока в месте к.з. (считая, что в месте металлического трехфазного к.з. имеется источник с э.д.с., равной нулю) получим

, (2.25)

где взаимные проводимости между каждым источником и точкой к.з.

Выражения (2.24) и (2.25) особенно удобны, когда нужно выявить индивидуальные свойства отдельных источников или учесть влияние изменения величины и фазы отдельных э.д.с. на искомые значения токов.

Собственные и взаимные сопротивления или проводимости находят с помощью так называемого способа токораспределения или путем преобразования исходной схемы замещения. Иногда целесообразно использовать оба приема совместно, то есть вначале произвести ряд преобразований схемы, а затем применить метод токораспределения.

В расчетах к.з. часто приходится определять только взаимные сопротивления между точкой к.з. и отдельными источниками (или группами их). Для этого удобно использовать следующий прием. Приняв ток в месте к.з. за единицу и считая все приведенные э.д.с. одинаковыми, нужно произвести распределение этого тока (равного единице) в заданной схеме замещения. Полученные доли этой единицы для отдельных источников: С, называемые коэффициентами распределения, при отсутствии нагрузок в схеме они характеризуют участия каждого источника в питании к.з. Если результирующее сопротивление схемы относительно места к.з. , то, очевидно, можно записать равенства:

1^. Z_, (2.26)

откуда искомое взаимное сопротивление между точкой к.з. и соответствующим источником будет:

Z_/С_n.