Лекция по теории систем 4

Лекция № 4.

Примеры определения весовой функции

1.Идеальная следящая система (ИСС).

.

Система не изменяет входное воздействие. В соответствии с принципом суперпозиции

весовая функция .

2.Идеальный экстраполятор.

, .

Система сдвигает входное воздействие на a временных единиц (эта система является примером физически неосуществимой системы, т. к. предсказывает те значения входного воздействия, которые на нее еще не поступали). Т.к. весовая функция и , то весовая функция .

3.Идеальная запаздывающая система.

,

Аналогично примеру 2, , но .

4.Идеальная дифференцирующая система (идеальный дифференциатор).

Система рассчитывает производную входного воздействия: Весовая функция рассчитывается в соответствии с определением

5.Идеальный интегратор.

Система рассчитывает интеграл от входного воздействия: .

Воспользуемся «близостью» форм записи реакции системы и реакции общей модели линейной системы:

. Поэтому (см. лекцию 3).

Многомерные системы. Описание в макроподходе

Система имеет m входов и n выходов:

В силу принципа суперпозиции, реакция системы по каждому выходу может быть определена как суперпозиция реакций на воздействие по каждому из входов.

Принцип суперпозиции позволяет рассмотреть одномерную систему, у которой входное воздействие u_i(t), а реакцию - y_k(t). Тогда составляющая реакции, определяемая входом i, равна:

а реакция по k выходу при приложении воздействия на вход i имеет вид:

.

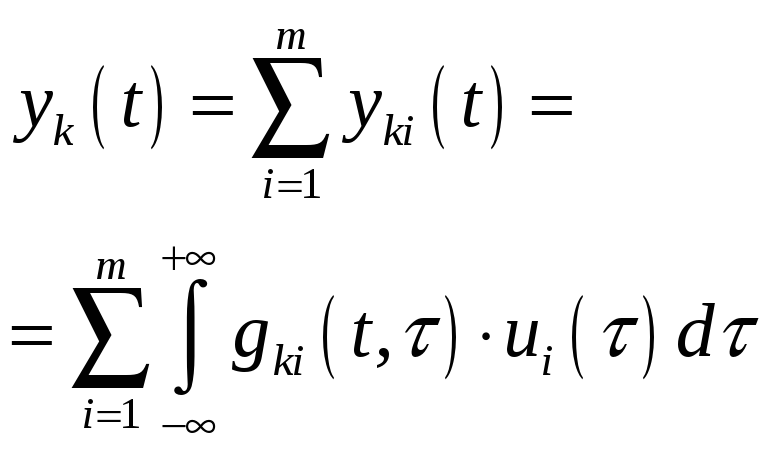С учетом линейности операторов суммирования и дифференцирования:

,

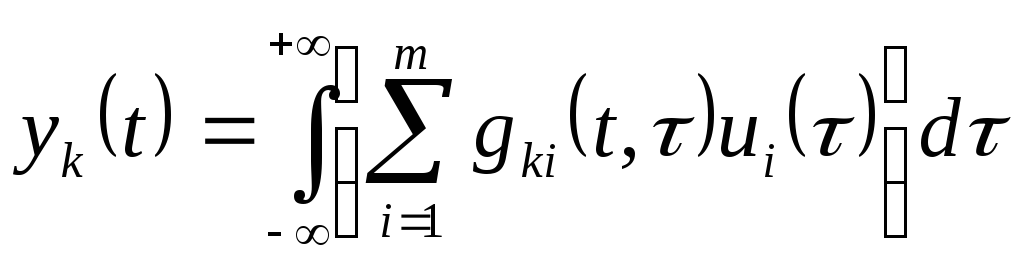- реакция по выходу

Введем в рассмотрение матрицу G:

-

матрицу импульсных переходных (весовых) функций;

вектор U: - вектор входных воздействий;

вектор Y: - вектор реакций системы.

Тогда имеем:

.

Таким образом, вновь получена структура математической модели, соответствующая результатам применения линейного оператора, но теперь для векторных входных воздействий и реакций.

Замечание 1. Очевидно, что процедура определения матрицы импульсных переходных функций может быть произведена с использованием импульсного воздействия, подаваемого на один из входов системы. Легко заметить, что при подаче импульсного воздействия в виде -функции на i-й вход многомерной системы на каждом из выходов с номером k () зафиксируется реакция в виде импульсной переходной функции , т.е. будет определен i-й столбец матрицы G.

Замечание 2. Для физически осуществимых систем , при , поэтому.