Лекция по теории систем 9

Лекция № 9. Решение уравнений состояния в частотной области

Решение уравнений состояния в частотной области основывается на применении преобразования Лапласа к обеим частям уравнений динамики и выхода и разрешения получившихся матричных уравнений относительно преобразования Лапласа вектора переменных состояния и выходной переменной системы.

Обозначим - оператор преобразования Лапласа. Он действует так:

(обозначения:

- преобразование Лапласа от ;

- преобразование Лапласа от ;

- преобразование Лапласа от ).

Применим этот оператор к обеим частям уравнения динамики . Получим:

. (1)

Применим оператор преобразования Лапласа к уравнению выхода .

Получим:

(2)

Разрешим уравнение (1) относительно :

или

Найденное решение подставим в уравнение выхода (2):

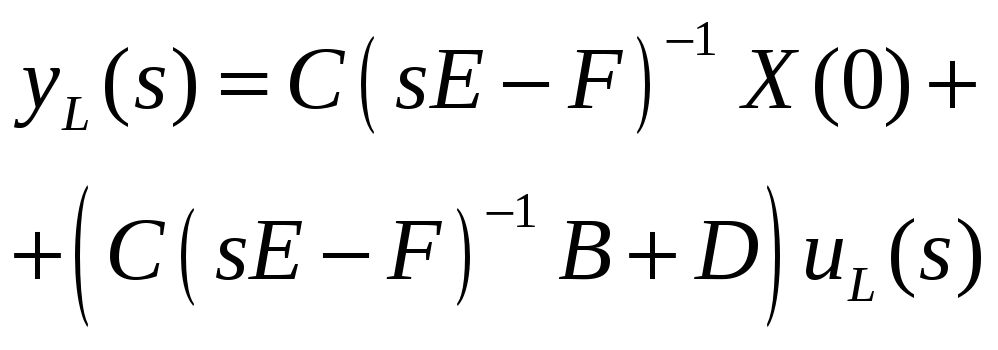(3)

Легко заметить, что первое слагаемое в найденном решении соответствует переходному процессу в системе и связано только с начальными условиями, а второе слагаемое соответствует вынужденному движению системы (частному решению неоднородного уравнения).

Задача1. Записать решение (3) для физически осуществимых систем

Задача2. Связать решение (3) с преобразованием Лапласа от полного решения линейного дифференциального уравнения n- порядка и найти связь между весовой функцией и и преобразованием Лапласа от фундаментальной матрицы

Пример решения уравнений состояния в частотной области.

Рассмотрим модель линейной системы, заданную дифференциальным уравнением 2-го порядка

Для нее основные матрицы:

Матрица

Обратную к ней матрицу определим как решение следующей системы уравнений:

.

Обозначим элементы искомой матрицы:

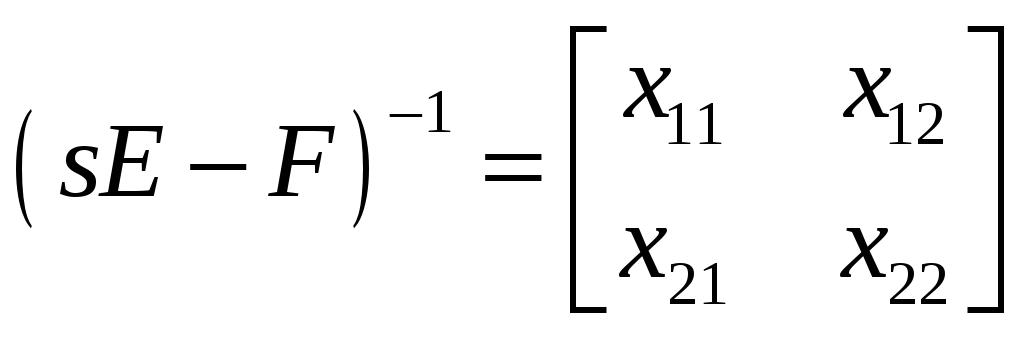
Тогда

.

Имеем две СЛАУ:

.

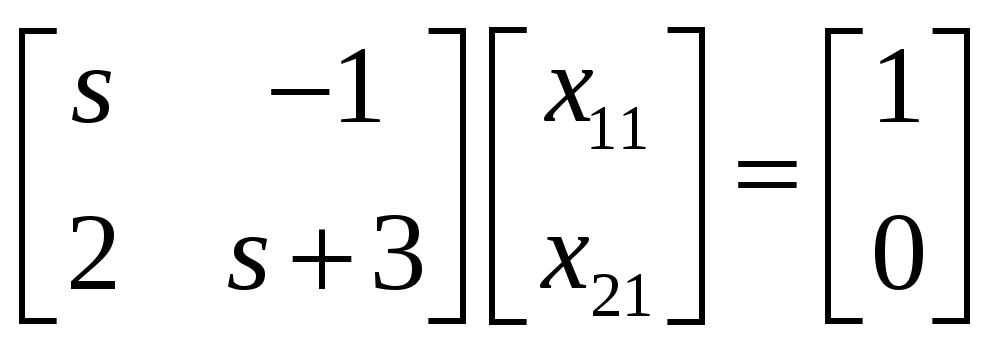
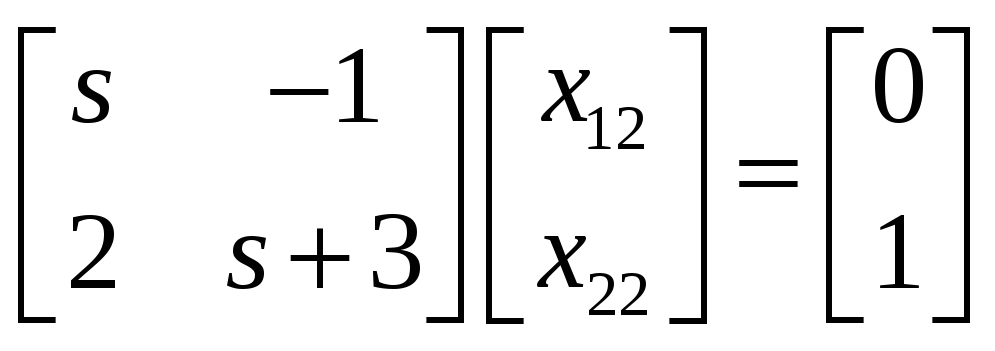В скалярной форме для первой системы уравнений:

.

; ;

; .

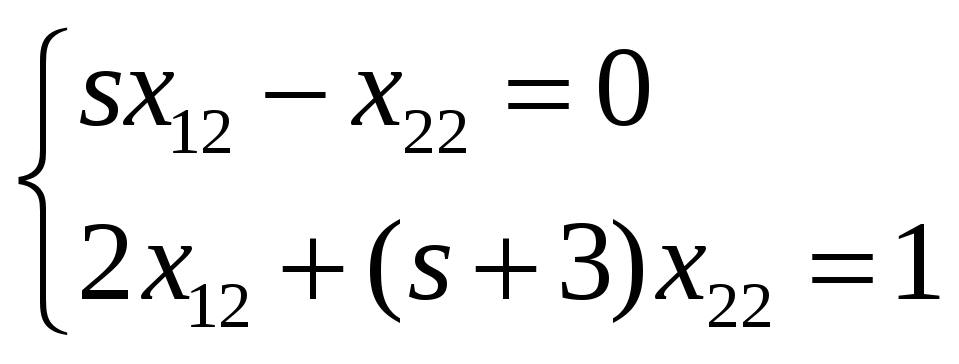В скалярной форме для второй системы уравнений:

;

.

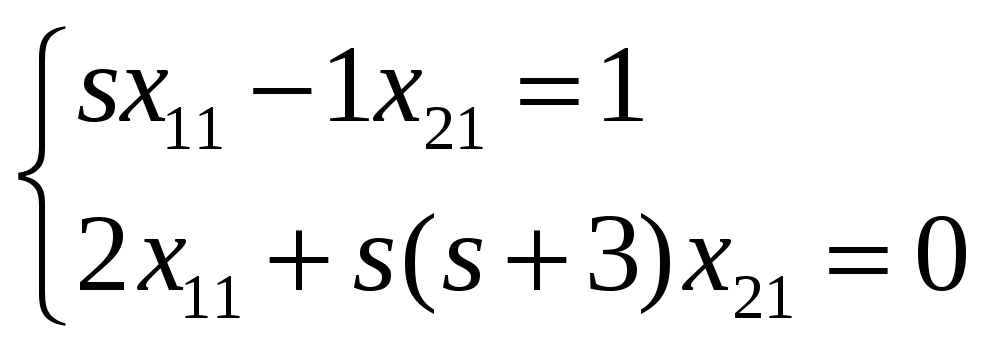
Получаем элементы обратной матрицы:

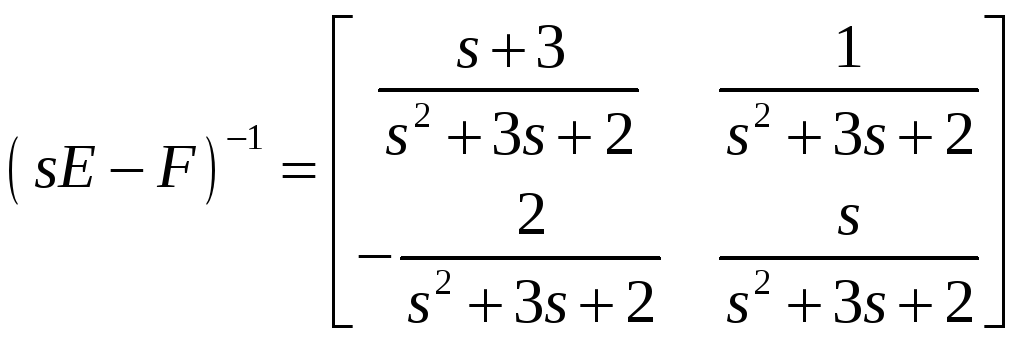
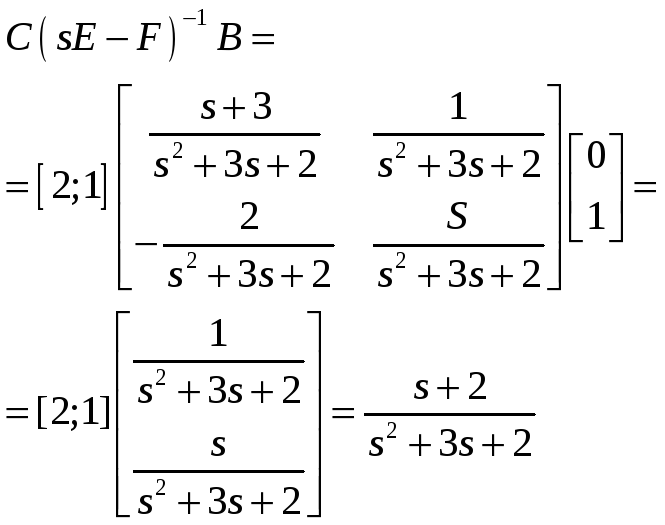
- есть изображение по Лапласу переходного процесса в системе. Установим связь между вектором начальными условиями задачи. Заметим, что .

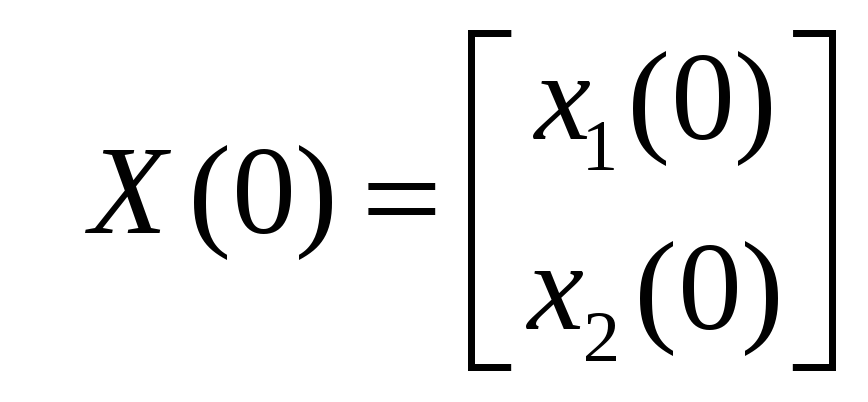С учетом результата предыдущей лекции:

В итоге получаем следующую систему уравнений:

.
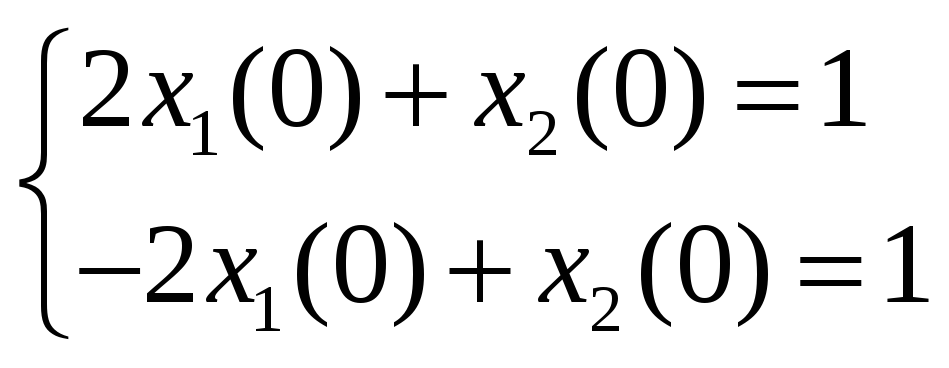