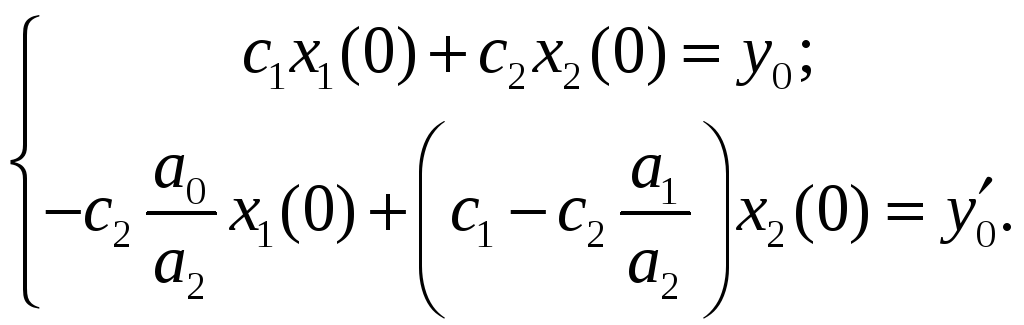Лекция по теории систем 8

Лекция №8. Решение уравнений состояния во временной обдасти

Рассмотрим решение матричного уравнения состояний во временной области:

с вектором началь-ных условий для переменных состояния .

Для решения этой задачи воспользуемся принципом суперпозиции, позволяющим нало-жить два решения: общее решение однородного уравнения и частное решение неоднородного уравнения: .

Как и раньше, будем искать решение однородного уравнения в виде , где С – вектор произвольных постоянных.

С учетом начальных условий: , - матричная экспонента, которая определяется разложением в матричный степенной ряд: . Обозначим: , тогда .

Функцию определяют как фундаментальную матрицу системы.

Будем искать решение неоднородного уравнения в виде: . Заметим: . Поэтому и, . Теперь решение неоднородного уравнения можно записать так: 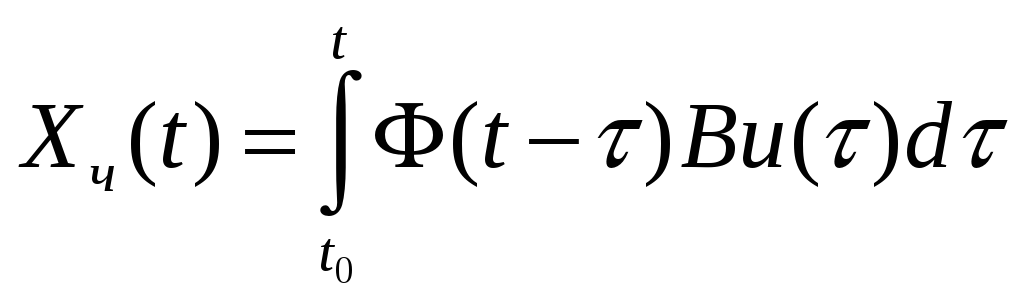, а полное решение уравнения соответственно .

Замечание1. При решении учтено, что

Замечание2. Для фундаментальной матрицы легко устанавливаются следующие свойства:

;

;

.

Подставим найденное решение уравнения динамики в уравнение выхода, получим:

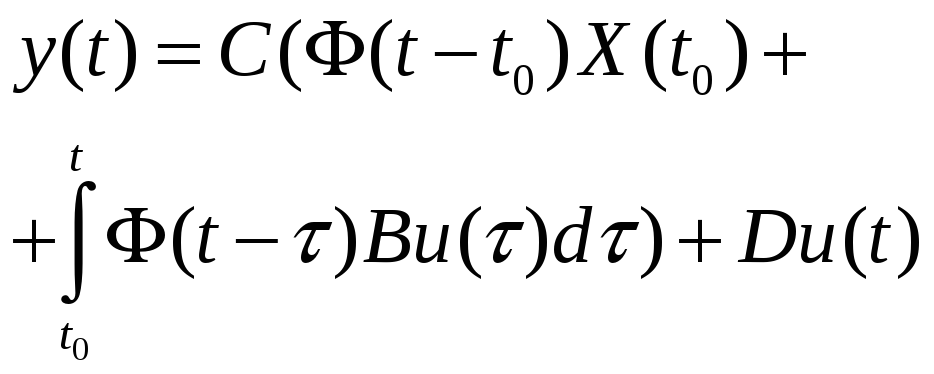или

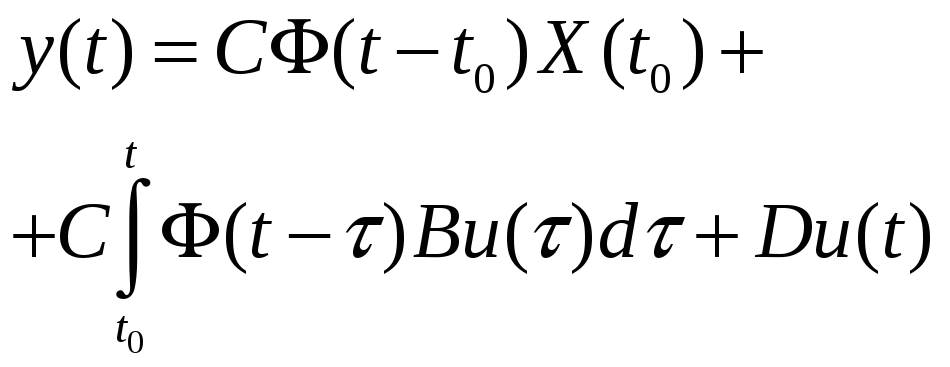
Полученное решение определяет решение уравнений состояния (динамики и выхода) во временной области.

Задача 1. Запишите соотношения, связывающие фундаментальную матрицу и весовую функцию исследуемой системы.

Задача 2. Как представить реакцию системы в виде интеграла свертки с учетом слагаемого .

Определение начальных условий при переходе от описания системы в макроподходе к описанию системы в микроподходе

При переходе в микроподход необходимо определить начальные условия для переменных состояния, которые соответствуют начальным условиям, заданным при описании системы линейным дифференциальным уравнением:

. Мы должны установить однозначное соответствие между этими начальными условиями и вектором начальных условий для переменных состояния (только для простоты выкладок положим ):

.

Для решения этой задачи воспользуемся уравнением выхода, в котором сохраним только общее решение однородного уравнения и в которое подставлено решение уравнения состояния :

. В этом решении есть искомый вектор начальных условий для переменных состояния.

Итак, после подстановки в уравнение выхода получим: . Напомним, что - есть фундаментальная матрица системы, задаваемая соотношением: .

Нам потребуются производные этой матрицы:

;;

.

Заметим, что при , где

E –есть единичная матрица. Поэтому

;;

.

Если теперь в решении последовательно определить производные и положить , то получим:

. (*)

Легко заметить, что полученная конструкция представляет собой систему линейных алгебраических уравнений (СЛАУ) относительно элементов вектора .

Таким образом, при поиске начальных условий для вектора переменных состояния по начальным условиям линейного дифференциального уравнения n - порядка необходимо решить СЛАУ вида (*)

Пример. При n=2 имеем:

В скалярной форме система уравнений примет вид: