Лекция по теории систем 15

Лекция №15. Многомерные линейные дискретные системы. Описание в макроподходе

Рассмотрим многомерную ЛДС.

Система имеет m входов и n выходов. В силу принципа суперпозиции, реакция системы по каждому выходу может быть определена как суперпозиция реакций на воздействие по каждому из входов.

Принцип суперпозиции позволяет рассмотреть одномерную систему, у которой входное воздействие u_i(k), а реакцию – y_j(k). Тогда составляющая реакции, определяемая входом i, равна:

а реакция по j выходу при приложении воздействия на вход i имеет вид:

С учетом линейности операторов суммирования:

- реакция по выходу ,.

Введем в рассмотрение матрицу G:

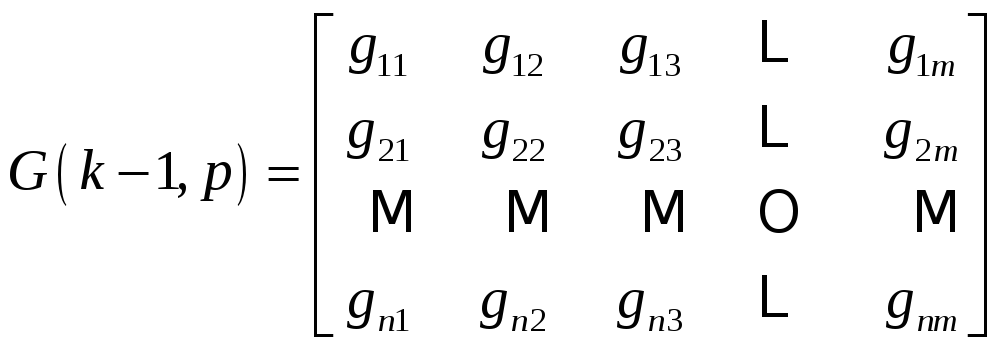- матрицу импульсных переходных (весовых) дискретных функций (последовательностей);

вектор U: - вектор входных воздействий;

вектор Y: - вектор реакций системы.

Тогда имеем:

.

Таким образом, вновь получена структура математической модели, соответствующая результатам применения линейного оператора, но теперь для векторных входных воздействий и реакций.

Замечание 1. Очевидно, что процедура определения матрицы импульсных переходных функций может быть произведена с использованием импульсного воздействия в виде символа Кронекера, подаваемого на один из входов системы. Легко заметить, что при подаче импульсного воздействия в виде символа Кронекера на i-й вход многомерной системы на каждом из выходов с номером j () зафиксируется реакция в виде импульсной переходной функции , т.е. будет определен i-й столбец матрицы G.

Замечание 2. Для физически осуществимых систем , при , поэтому .

Решение уравнений состояния для линейных дискретных систем во временной области

Рассмотрим линейную дискретную систему, которая имеет l входов и m выходов.

В макроподходе:

В микроподходе

- уравнение динамики;

- уравнение выхода; ; ; ; ; ; .

Вектор - задан. Решим уравнения состояния, последовательно изменяя номер определяемого члена последовательности :

:

:

:

Эти расчеты позволяют предположить, что:

Подставим найденный вектор в уравнение выхода:

Или

где 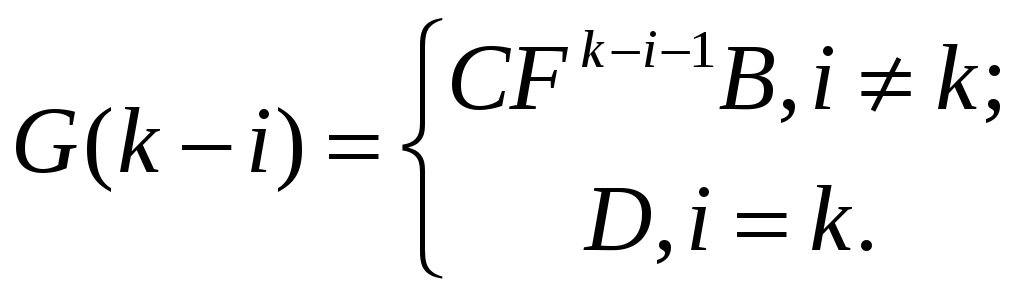- матрица дискретных весовых функций (последовательностей).

Т.к. для физически осуществимых систем матрица D должна равняться нулю, то , и матрицы C, F, B связаны с матрицей дискретных весовых функций соотношением: