Лекция по теории систем 12

Лекция №12. Линейные дискретные системы

Под линейными дискетными системами (ЛДС) будем понимать системы, у которых входные и выходные функции (или и то и другое) являются дискретными функциями времени и для которых выполнен принцип суперпозиции.

Вопрос: Как выглядит принцип суперпозиции в дискретной форме?

Рассмотрим представление линейных дискретных систем, как с точки зрения макроподхода, так и с точки зрения микроподхода.

Линейные дискретные системы. Описание с помощью макроподхода

Приведем простейший пример, который покажет, как при подготовке моделирования линейной непрерывной системы на ЭВМ появляется ЛДС.

Рассмотрим ЛДУ 2-го порядка в дискретные моменты времени :

.

Оценим производные с помощью конечных разностей:

Обозначим , тогда уравнение приобретает вид (в предположении, что узлы равноотстоящие, и ):

Если ввести коэффициенты: ; ; , то получим т.н. разностное уравнение 2-го порядка:

Основной математической моделью является линейное разностное уравнение (ЛРУ) порядка n: Линейное разностное уравнение порядка n имеет вид:

(1)

В компактном виде: .

В операторной форме: , где , - линейные операторы, а - линейный оператор сдвига

Решить уравнение (1) - найти последовательность , которая при подстановке в уравнение образует верное равенство.

Аналогично дифференциальным уравнениям для однозначного решения уравнения (1) должны быть заданы n начальных условий .

Рассмотрим ЛРУ 1-го порядка:

Разрешим уравнение относительно и непосредственной подстановкой различных значений k «угадаем» решение для произвольного значения номера:

Положим: и .

При

при

при

Эти расчеты позволяют предположить, что:

Из примера следует, что, с одной стороны последовательность решения может быть найдена непосредственно подстановкой значений k для y, а с другой стороны - в виде явного выражения связанного с y₀ и значениями входного воздействия.

Из примера также следует, что полное решение разностного уравнения снова может быть представлено в виде суперпозиции двух видов решений:

- решение связанное только с начальным условием; его будем называть общим решением однородного уравнения;

- решение связанное только с входными воздействиями; его будем называть частным решением неоднородного уравнения (вынужденным решением).

Следует также ожидать, что для линейного разностного уравнения удастся предложить аппарат решения похожий на аппарат решения дифференциального уравнения.

Для нахождения частного решения неоднородного разностного уравнения применим принципы, использованные для нахождения частного решения неоднородного дифференциального уравнения (придем к аналогу весовой функции для дискретных систем).

Рассмотрим следующую последовательность

Свяжем элементы этой последовательности друг с другом, используя принцип суперпозиции в дискретной форме:

. Легко заметить, что функция

Эта функция носит специальное название символа Кронекера и обозначается . Символ Кронекера играет туже роль, что, и - функция для непрерывных систем, и он может быть использован в качестве элементарного воздействия для определения какой-то характеристики линейной дискретной системы, которую назовем по аналогии с непрерывными системами весовой функцией системы (весовой последовательностью).

Принцип суперпозиции позволяет определить реакцию дискретной системы, как результат воздействия оператора системы на входную последовательность. Считая, что реакция системы определяется через воздействие , применим оператор системы A к воздействию :

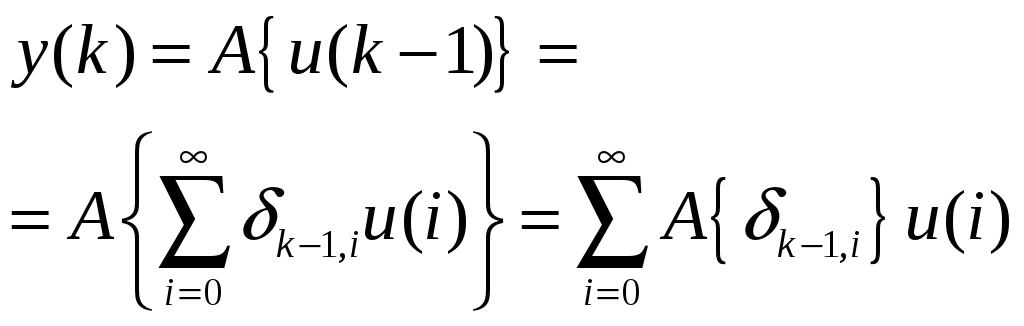
Заметим, что оператор A применяется к элементарному воздействию в виде символа Кронекера. По аналогии с непрерывными системами назовем весовой функцией системы. Поэтому реакция системы может быть представлена в виде:

, что представляет собой аналог интеграла свертки для непрерывных систем.

Если система физически осуществима, то

_. Если система описывается ЛРУ с постоянными коэффициентами, то ее весовая функция может быть определена как функция одного аргумента, а именно, реакция примет вид:

_.