8.2. Структурные схемы системы тп-д

На рис.8.6, а представлена структурная схема системы управления двигателем постоянного тока с вентильным (тиристорным) преобразователем, состоящая из преобразователя и двигателя . В этой схеме - наименьшая постоянная времени (постоянная времени преобразователя); и - электромагнитная и электромеханическая постоянные времени двигателя, подлежащие компенсации.

Следовательно, чтобы скомпенсировать их влияние на динамику системы, необходимо применение двух контуров регулирования (рис. 8.6, б): внутренний контур регулирования тока с регулятором тока и внешний контур регулирования скорости с регулятором скорости .

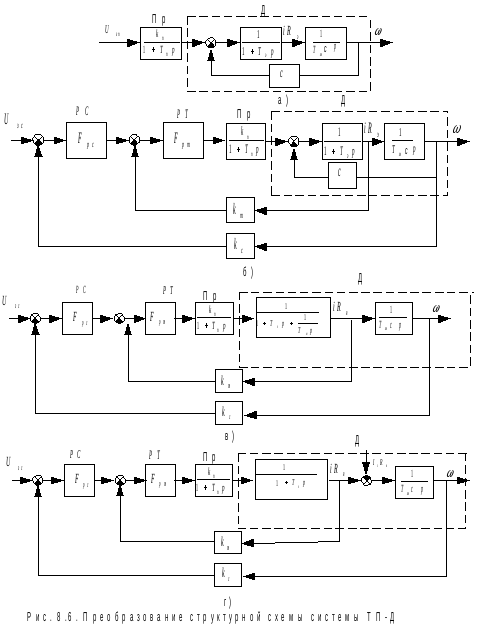
Для удобства преобразуем схему рис. 8.6,б в схему рис. 8.6, в.

Пользуясь (8.10), найдем передаточную функцию регулятора тока

.

(8.14)

Если существенно больше (примерно в два раза и более), то в числителе уравнения (8.14) можно пренебречь третьим членом и тогда передаточная функция регулятора тока будет иметь вид

.

(8.15)

При указанном допущении можно пользоваться схемой рис. 8.6, г, в которой опущена внутренняя обратная связь двигателя, что приводит к значительному упрощению расчетов параметров системы.

Передаточная функция регулятора скорости определяется по (8.14), где ; ;

,

(8.16)

где -коэффициент ЭДС (момента) двигателя при номинальном магнитном потоке; и - ЭДС и скорость идеального холостого хода; и - номинальные момент и ток двигателя.

Подставляя рассчитанные значения передаточных функций регуляторов в схему рис. 8.6, г, получаем оптимальную структурную схему, для которой действительна передаточная функция

(8.17)

и соответствующая ей переходная функция (таблица 8.1), т.е.

,

(8.18)

где - скорость идеального холостого хода двигателя; - текущее значение скорости.

Учитывая , что , после соответствующих преобразований поучаем

,

(8.19)

где - относительное время; - действительное время.

На рис.8.7 представлены кривые переходного процесса скорости и тока двигателя, рассчитанные по уравнениям (8.18) и (8.19).

8.3. Влияние нагрузки на работу системы

Момент статического сопротивления и управляющий сигнал приложены в разных местах системы (рис 8.8, г), поэтому поведение системы при воздействии со стороны нагрузки не аналогично поведению системы при воздействии со стороны управления.

Исходное уравнение для системы ТП-Д (рис. 8.6, г) с учетом действия сигнала управления и сигнала нагрузки имеет вид

,

где - передаточная функция замкнутого контура тока; - передаточная функция регулятора скорости.

Для определения влияния на систему только нагрузки в этом уравнении следует положить . Обозначив изменение скорости двигателя, связанное с воздействием нагрузки, через , получим

,

откуда

.

(8.20)

После соответствующих преобразований в (8.20) напишем

.

(8.21)

Учитывая, что

(8.22)

и исключая из (8.26), будем иметь

.

(8.23)

где - относительное изменение скорости;

- естественный статический перепад скорости.

Уравнению (8.23) соответствует переходная функция

,

(8.24)

а уравнению (8.21)

,

(8.25)

В последних уравнениях .

По уравнениям (8.24) и (8.25) рассчитаны переходные функции для двух контурной системе, настроенной на модульный оптимум, при ударном приложении нагрузки (исходные постоянные времени: ; ).

Результаты расчетов представлены на рис. 8.10. Установившийся перепад скорости в замкнутой системе зависит от соотношения постоянных времени и , для рассматриваемого случая:

Рис. 8. 10. Кривые переходного процесса относительного тока () и относительного перепада скорости () в двух контурной системе, настроенной на модульный оптимум, при ударном приложении нагрузки

Рис. 8. 11. Кривые переходных процессов относительного перепада скорости () в двух контурной системе, настроенной на модульный оптимум, при ударном приложении нагрузки для трех различных значений постоянных времени

На рис. 8.11 представлены кривые перепада скорости для трех значений (кривая 1 –; кривая 2 - ; кривая 3 - ), для всех трех случаев .

Если статизм, получаемый в двухконтурной системе, настроенной по модульному оптимуму, не удовлетворяет требованиям технологии, то рекомендуется применять не пропорциональный, а интегрально-пропорциональный регулятор скорости, при котором система превращается из статической в астатическую, настроенную на симметричный оптимум.

Для астатической системы ТП-Д (рис 8.12) передаточная функция регулятора скорости

.

(8.26)

Передаточная функция регулятора содержит форсирующее звено , которое форсирует переходный процесс в сравнении со статической системой при воздействии со стороны управления. Для компенсации его влияния необходимо на вход системы установить инерционное звено с передаточной функцией

.

(8.28)

Рис.8. 12. Структурная схема астатической системы регулирования скорости

Передаточная функция системы ТП-Д с интегрально-пропорциональным регулятором скорости при воздействии со стороны нагрузки имеет вид:

для перепада скорости

,

(8.29)

для тока двигателя

.

(8.30)

Переходные функции, соответствующие приведенным уравнениям будут иметь вид:

,	(8.41)
,	(8.42)

где .

На рис 8.13 построены кривые изменения скорости и тока при ударном приложении нагрузки в астатической системе с ИП-регулятором скорости.

Рис. 8.13. Кривые переходного процесса относительного тока () и относительного перепада скорости () в двухконтурной системе, настроенной по симметричному оптимуму, при ударном приложении нагрузки