21. Глобальная интерполяция

 При глобальной интерполяции ищется единый полином для всего интервала. Если среди узлов {x_i,y_i} нет совпадающих, то такой полином будет единственным, и его степень не будет превышать n.

Запишем систему уравнений для определения коэффициентов полинома

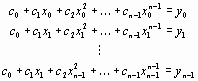
Определим матрицу коэффициентов системы уравнений 

Решим систему уравнений матричным методом

Определим интерполяционный полином

Представим результаты на графике

Вычислим значения интерполяционного полинома в заданных точках и сравним их с точными значениями

 

Коэффициенты интерполяционного полинома следующие:

Внимание! Из-за накопления вычислительной погрешности (ошибок округления) при большом числе узлов (n>10) возможно резкое ухудшение результатов интерполяции. Кроме того, для целого ряда функций глобальная интерполяция полиномом вообще не дает удовлетворительного результата. Рассмотрим в качестве примера две таких функции. Для этих функций точность интерполяции с ростом числа узлов не увеличивается, а уменьшается. Первым примером является функция . Построим для нее интерполяционный полином на интервале [–1;1], используя 9 точек.

 

 

22. Интерполяционный полином Лагранжа.

Лагранж предложил строить интерполяционный полином в виде разложения

Где l_i(x) – базисные функции.

Для того, чтобы полином, записанный в форме (4.4), удовлетворял условиям Лагранжа, т.е. был бы интерполяционным, базисные функции l_i(x) должны обладать следующими свойствами:

1) быть полином степени n 2) удовлетворять условию .

Лагранж показал, что функции, обладающие указанными свойствами, должны иметь следующий вид

С учетом выражения интерполяционный полином Лагранжа может быть записан в виде

В отличии от интерполяционного полинома в канонической форме для вычисления значений полинома Лагранжа не требуется предварительно определять коэффициенты полинома путем решения системы уравнений. Однако для каждого значения аргумента x полином Лагранжа приходится пересчитывать вновь, коэффициенты же канонического полинома вычисляются только один раз. Поэтому практическое применение полинома Лагранжа оправдано только в том случае, когда интерполяционная функция вычисляется в сравнительно небольшом количестве точек x.

Ø Замечание. Интерполяционный полином Лагранжа оказывается очень удобным для приближенного вычисления определенных интегралов. Если, например, некоторую функцию заменить интерполяционным полином Лагранжа , то определенный интеграл от нее может быть вычислен следующим образом . Значения интегралов от l_i(x) не зависят от f(x) и могут быть легко вычислены аналитически.<

23. Интерполяционный полином Ньютона.

Рассмотрим еще одну форму записи интерполяционного полинома

Требования совпадения значений полинома с заданными значения функции в узловых точках , приводит к системе линейных уравнений с треугольной матрицей для неизвестных коэффициентов :

решение которой не составляет труда.

Интерполяционный полином, записанный в форме (4.7), называется полиномом Ньютона. Интересная особенность полинома Ньютона состоит в том, что каждая частичная сумма его первых слагаемых представляет собой интерполяционный полином степени m, построенным по первым (m+1) типичным данным.