Презентации по математике / Лекции 1 семестр / 2. Лекция 3 Элементы векторной алгебры
.docЛекция №3 «Элементы векторной алгебры»
Векторная алгебра изучает векторные величины, то есть величины, имеющие модуль и направление.
Определение: Любые две точки пространства, если они упорядочены, определяют отрезок с заданным на нем направлением. Направленный отрезок называется вектором.
Длиной (модулем)
вектора
называется длина отрезка AB
и обозначается
Определение: Вектором называется любой параллельный перенос в пространстве.
Классификация векторов
1. Векторы называются равными, если их модули равны, и они одинаково направлены.
Два направленных отрезка АВ и CD изображают один и тот же вектор, если их длины равны, прямые (АВ) и (CD) параллельны (в т.ч. совпадают), а направление от А к В одинаково с направлением от C к D.Таким образом, направленных отрезков, изображающих один и тот же вектор, бесконечное множество.
2. Вектор, длина
которого равна нулю, называется нулевым
и обозначается
.
3. Вектор, длина
которого равна единице, называется
единичным (или ортом) и обозначается
.
4. Векторы называются противоположными, если они одинаковы по модулю, но противоположны по направлению.
5. Два ненулевых вектора называются коллинеарными, если они могут быть изображены направленными отрезками параллельных прямых (в т.ч., одной и той же прямой).
6. Три ненулевых вектора называются компланарными, если они могут быть изображены направленными отрезками, принадлежащими параллельным плоскостям (в том числе, одной и той же).
Линейные операции над векторами
1. Сложение векторов
Правило
треугольника:Суммой
двух векторов
и
называется
вектор, начало которого лежит в начале
вектора
и
конец в конце вектора
.
картинка
Правило
параллелограмма: Если
векторы отложены от общего начала и на
них построен параллелограмм, то суммой
векторов
и
является вектор, совпадающий с
вектором-диагональю этого параллелограмма,
идущей из общего начала векторов
и
.
Картинка
2. Вычитание векторов
3. Умножение вектора на число.
Определение:
Произведением вектора
на число
называется вектор
такой, что: 1)
;
2)
,
если
и
,
если
Проекция вектора на ось.
Пусть даны ось L
и вектор
.
Обозначим через А’ и В’ соответственно
проекции точек А и В на ось L.
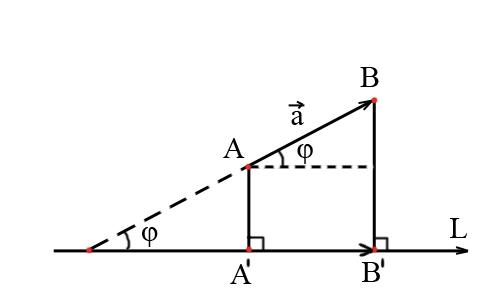
Проекцией вектора
на
ось L
называется число, равное длине вектора
,
взятое со знаком «+», если направления
вектора
и
оси L
совпадают, и со знаком «-» в противном
случае.
Аналогично определяется проекция вектора на вектор.
Справедлива
формула:
,
где φ – угол между вектором и осью
Задача:
Найти проекцию
вектора
на вектор
.
Решение.
Известно, что
пр
.
Косинус угла между
векторами
и
Следовательно
Пр
.
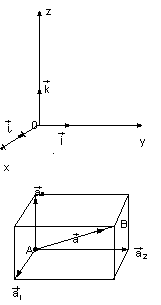
Координаты вектора
Введем единичные векторы (орты) i, j, k , направленные по осям координат. Они не равны, так как являются единичными векторами неколлинеарных векторов.
Рассмотренные выше линейные операции над векторами можно теперь записать в следующем виде:
-
При умножении вектора на скаляр координаты вектора умножаются на этот скаляр.
-
При сложении (вычитании) векторов их одноименные координаты складываются (или вычитаются).
3) Векторы коллинеарны тогда и только тогда, когда их одноименные координаты пропорциональны.
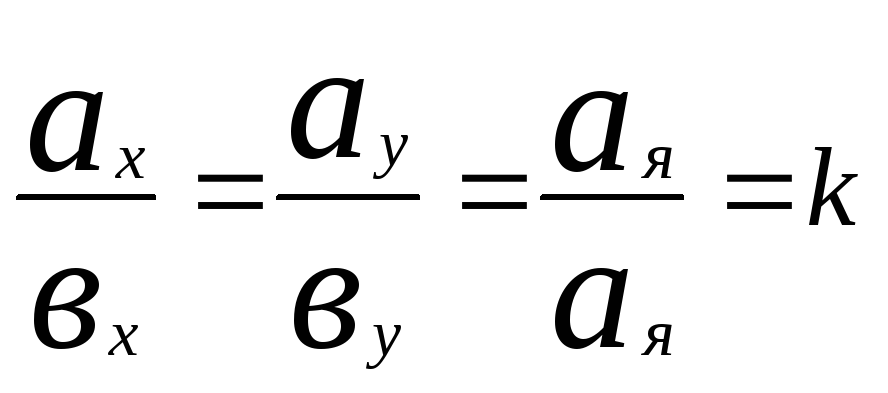
Задача: Проверить
коллинеарность векторов
и
Решение:
Если векторы
и
коллинеарны, то должно выполняться
условие
=
или в координатной форме
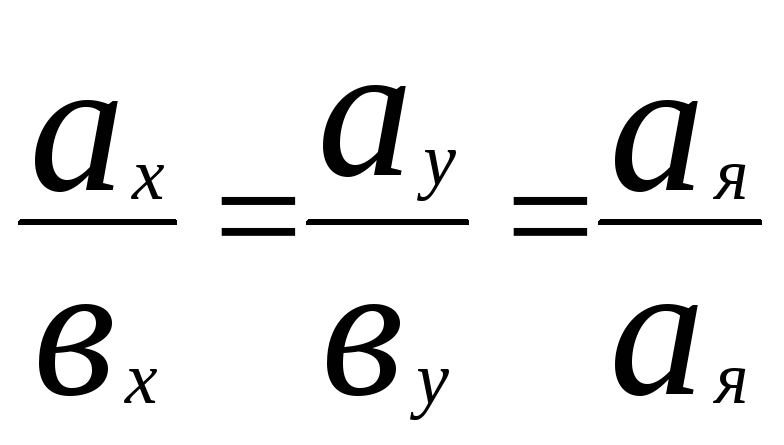
Для заданных
векторов
,
следовательно
векторы
и
коллинеарны. При этом
и
,
то есть модуль вектора
равен
модуля
.
Знак “-“ указывает, что векторы направлены
в противоположные стороны.
Длина (модуль) вектора равна корню квадратному из суммы квадратов его координат.
Задача:По
данным векторам
и
найти координаты вектора
=2
+5
Решение:
=2
+5
=2(3
-4
+5
)+5(-
-2
)=6
-8
+10
-5
-10
=
-8
+0
.
Вектор
=
-8
.
Его координаты
Скалярное произведение векторов.
Def: Под скалярным произведением двух векторов и понимается число, равное произведению длин этих векторов на косину угла между ними, т.е
Скалярное произведение в координатной форме.
Скалярное произведение векторов равно сумме парных произведений их одноименных координат
Задача: Найти скалярное произведение векторов
и
и угол
между ними.
Решение.
По формуле
найдем скалярное произведение
.
Используя формулу (1), найдем длины векторов
,
.
Тогда по формуле
найдем косинус
угла
,
отсюда
.
Векторное произведение векторов
Под
векторным произведением двух векторов
понимается вектор
, для которого:
Модуль векторного произведения двух векторов равен площади параллелограмма, построенного на этих векторах.
Э
тот
вектор перпендикулярен перемножаемым
векторам (перпендикулярен плоскости
параллелограмма), т.е и
Векторное произведение в координатной форме
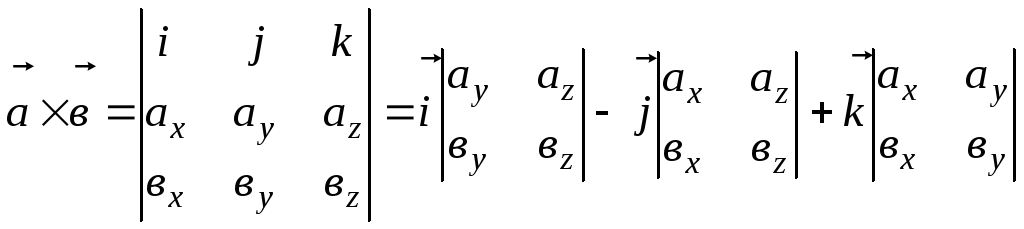
Вычислить модуль
векторного произведения векторов
и
.
Решение.
По формуле
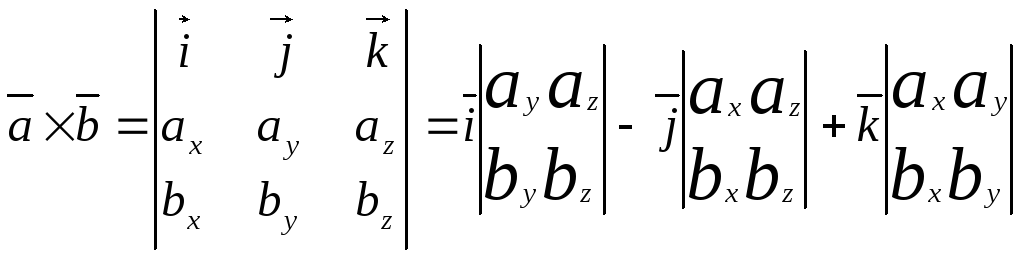
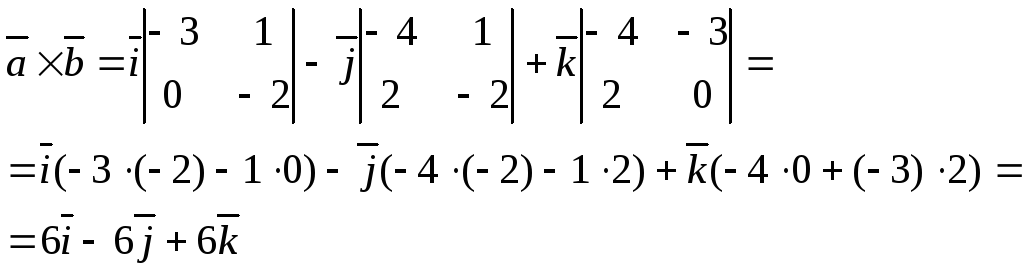
Тогда модуль
векторного произведения
равен
.
-
Геометрический смысл векторного произведения.
Задача 1
Найти площадь
параллелограмма, построенного на
векторах
и
.
Решение.
Используя формулу
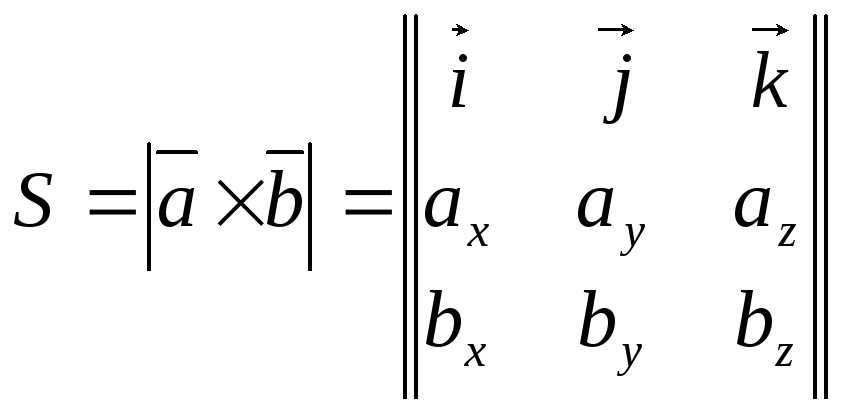
получим
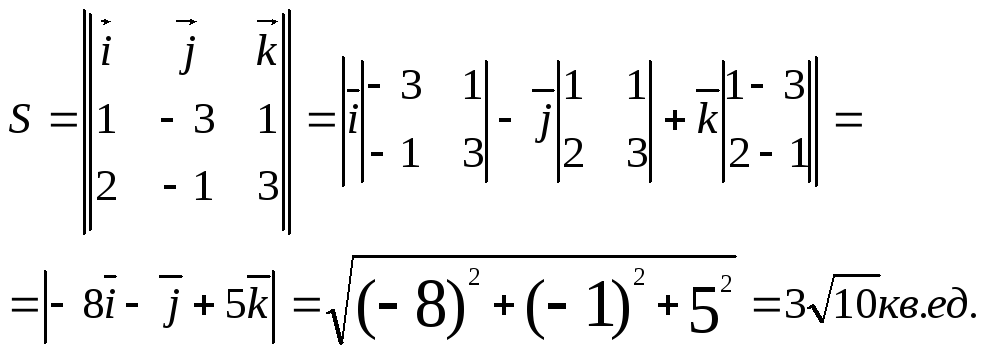
Задача: Вычислить площадь треугольника ABC, если А(-2,1,3),
В(2,-1,7), С(11, 2, -5).
Решение.
Используя координаты вершин треугольника, находим
Тогда
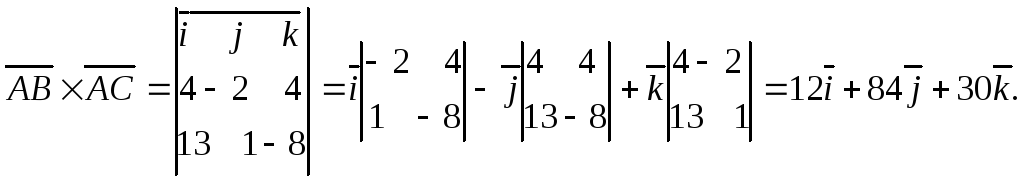
