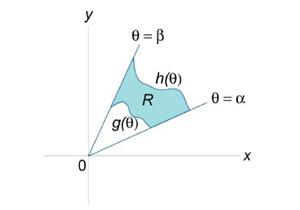
Геометрический смысл двойного интеграла

Пусть функция принимает в области только положительные значения. Тогда двойной интеграл 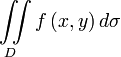численно равен объему вертикального цилиндрического тела, построенного на основании и ограниченного сверху соответствующим куском поверхности .

Физический смысл

Если рассматривать перемещение, то первая производная - скорость, вторая - ускорение. Соответственно, интеграл от ускорения - это скорость, двойной интеграл - перемещение. Если рассмотреть график ускорения, то двойной интеграл от него - площадь под графиком.

40-основные свойства двойного интеграла

1°. Аддитивность. Если функция f(x, y) интегрируема в области D и если область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области D₁ и D₂, то функция f(x, y) интегрируема в каждой из областей D₁ и D₂, причем

     2°. Линейное свойство. Если функции f(x, y) и g(x, y) интегрируемы в области D, а α и β - любые вещественные числа, то функция [α · f(x, y) + β · g(x, y)] также интегрируема в области D, причем

     3°. Если функции f(x, y) и g(x, y) интегрируемы в области D, то и произведение этих функций интегрируемо в D.

     4°. Если функции f(x, y) и g(x, y) обе интегрируемы в области D и всюду в этой области f(x, y) ≤ g(x, y), то

     5°. Если функция f(x, y) интегрируема в области D, то и функция |f(x, y)| интегрируема в области D, причем

(Конечно, из интегрируемости |f(x, y)| в D не вытекает интегрируемость f(x, y) в D.)

     6°. Теорема о среднем значении. Если обе функции f(x, y) и g(x, y) интегрируемы в области D, функция g(x, y) неотрицательна (неположительна) всюду в этой области, M и m - точная верхняя и точная нижняя грани функции f(x, y) в области D, то найдется число μ, удовлетворяющее неравенству m ≤ μ ≤ M и такое, что справедлива формула

(11)

     В частности, если функция f(x, y) непрерывна в D, а область D связна, то в этой области найдется такая точка (ξ, η), что μ = f(ξ, η), и формула (11) принимает вид

     7°. Важное геометрическое свойство. равен площади области D (Это свойство, как уже отмечалось ранее, непосредственно вытекает из определения интегрируемости, данного в пункте Определение и существование двойного интеграла для произвольной области)

41-вычисление двойного интеграла в декартовых координатах.

Область D называется правильной в направлении оси OY (ОХ), если любая прямая, параллельная оси OY(OX) и проходящая через внутреннюю точку области Д пересекает ее границу в двух точках.

Рис. 23.3

Рис. 23.4

Граница области D, правильной в направлении оси OY (рис. 23.3), может быть задана уравнениями

 и двойной интеграл в этом случае вычисляется по формуле

 (23.5)

причем сначала вычисляется внутренний интеграл

в котором х считается постоянной. Выражение справа в (23.5) называется повторным, или двукратным интегралом.

Граница области D, правильной в направлении оси ОХ (рис. 23.4), может быть задана уравнениями:

 Тогда двойной интеграл вычисляется по формуле

 (23.6)

Если область D правильная в направлении ОХ и OY (правильная область), то применимы обе формулы.

Рассмотрим геометрический смысл формулы (23.5), для формулы (23.6) рассуждения аналогичные (вывод формул приведен в [6. С. 310]).

Предположим, чтои граница области D является правильной в направлении оси OY.

Из разд. 23.1

Подсчитаем теперь объем V методом поперечных сечений (см. п.18.2.1):

 (23.7)

Проводя через т. (х,0,0) плоскость перпендикулярно оси ОХ, получим в сечении криволинейную трапецию

(рис. 23.5), с площадью

для точек линиипри постоянном х зависит только от у:

 - (23.8)

площадь поперечного сечения цилиндрического тела. Подставляя (23.8) в (23.7), получаем

Рис. 23.5

Таким образом, в формуле (23.7) слева и справа имеем объем цилиндрического тела.

Формулы (23.5) и (23.6) выведены в предположении, что область имеет специальный вид.

В общем случае область D разбивают на конечное число частей, являющихся правильными, и вычисляют для каждой из частей интеграл по формуле (23.5) или (23.6). Интеграл по всей области (свойство 3°) равен сумме полученных интегралов.

Если область ГУ.то формулы (23.5) и (23.6)

примут вид

Пример:

Решение разбивается на три этапа:

1) построение области D;

2)  переход к повторному интегралу, расстановка пределов интегрирован ия;

3)  вычисление повторного интеграла.

Решая системунаходим т. пересечения параболы

и прямой (1, 1), (-2, 4). Строим область, (-2, 4)D (рис. 23.6). Так как область правильная, то можно воспользоваться формулами (23.5) и (23.6).

При решении по (23.5) область придется разбить на две: ОВС и СВА, так как линия ОБА задается разными уравнениями:

Рис. 23.6

При вычислении по формуле (23.6) приходим к одному повторному интегралуЗакончим

решение, пользуясь последней формулой:

42-Вычисление двойного интеграла в полярных координатах.

Одним из частных случаев замены переменных является переход из декартовой в полярную систему координат (рисунок 1).

Рис.1		Рис.2

Якобиан такого преобразования имеет вид

Следовательно, дифференциальный элемент в полярных координатах будет равен

Пусть область интегрирования R в полярных координатах определяется следующим образом (рисунок 2):

Тогда двойной интеграл в полярных координатах описывается формулой

Будем называть полярным прямоугольником область интегрирования, показанную на рисунке 3 и удовлетворяющую условиям

В этом случае формула замены переменных в двойном интеграле имеет вид

43-Приложения двойного интеграла (объем тела, плоской фигуры, масса, статические моменты, координаты центра тяжести, момент инерции)

Приложения двойного интеграла

Приведем некоторые примеры применения двойного интеграла.

Объем тела

Как уже показано (п. 7.2), объем цилиндрического тела находится по формуле

где z=ƒ(х;у) - уравнение поверхности, ограничивающей тело сверху.

Площадь плоской фигуры

Если положить в формуле (7.4) ƒ(х;у)=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н=1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:

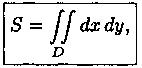
или, в полярных координатах,

Масса плоской фигуры

Как уже показано (п. 7.2), масса плоской пластинки D с переменной плотностью g=g(х;у) находится по формуле

Статические моменты и координаты центра тяжести плоской фигуры

Статические моменты фигуры D относительно осей Ох и Оу (см. Часть 1, п. 41.6) могут быть вычислены по формулам

а координаты центра масс фигуры - по формулам

Моменты инерции плоской фигуры

Моментом инерции материальной точки массы м относительно оси l называется произведение массы м на квадрат расстояния d точки до оси, т. е. Мl=m • d². Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:

Момент инерции фигуры относительно начала координат - по формуле М_о=М_х +М_у.

Замечание. Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 11.3).

44-Тройной интеграл.Теорема существования.

Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл».

Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.Пусть в замкнутой области V пространства Oxyz задана непрерывная функция u=ƒ(х;у;z). Разбив область V сеткой поверхностей на n частей и выбрав в каждой из них произвольную точку М_i(х_i;y_i;z_i), составим интегральную суммудля функции ƒ(х; у; z) по

области V (здесь ∆V_i - объемэлементарной области V_i).

Если предел интегральной суммы существует при неограниченном увеличении числа n таким образом, что каждая «элементарная область» Vi стягивается в точку (т. е. диаметр области d_i стремится к нулю, т. е. di-> 0), то его называют тройным интегралом от функции u=ƒ(х;у;z) по области V и обозначают

Таким образом, по определению, имеем:

Здесь dv=dx dy dz - элемент объема.

Теорема 8.1 (существования). Если функция u=f(x;y;z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (8.1) при n->∞ и max di -> 0 существует и не зависит ни от способа разбиения области V на части, ни от выбора точек M_i(x_i,y_i,z_i) в них.

Тройной интеграл обладает теми же свойствами, что и двойной интеграл:

1. 

2. 

3. если V=V₁ È V_2, а пересечение V₁ и V₂ состоит из границы, их разделяющей.

4. если в области V функция f(x;y;z)>=0. Если в области интегрирования ƒ(х;у;z)>=j(x;y;z), то и

5 ., так как в случаелюбая интегральная сумма имеет види численно равна объему тела.

6. Оценка тройного интеграла:

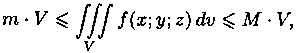
где m и М - соответственно наименьшее и наибольшее значения функции f(x;y;z) в области V.

7. Теорема о среднем значении: если функция f(x;y;z) непрерывна в замкнутой области V, то в этой области существует такая точка M_o(x_o;y_o;z_o), что

где V - объем тела.

45-Вычисление тройного интеграла в декартовых координатах

Вычисление тройного интеграла в декартовых координатах сводится к последовательному вычислению трех определенных интегралов.  Рассмотрим случай, когда область интегрирования U является элементарной относительно оси Oz, т.е. любая прямая, параллельная оси Oz, пересекает границу области U не более, чем в двух точках. Пусть областьU ограничена снизу поверхностью z = z₁(x,y), а сверху - поверхностью z = z₂(x,y) (рисунок 1). Проекцией телаU на плоскость Oxy является область D (рисунок 2). Будем предполагать, что функции z₁(x,y) и z₂(x,y)непрерывны в области D.

Тогда для любой непрерывной в области U функции f (x,y,z) можно записать соотношение

Таким образом, вычисление тройного интеграла сводится к вычислению двойного интеграла, в котором подынтегральной функцией является однократный интеграл. В рассмотренном случае сначала вычисляется внутренний интеграл по переменной z, а затем - двойной интеграл в области D по переменным x и y.  Если область D(x,y) является областью типа I (смотрите Повторные интегралы), т.е. ограничена линиями

где f₁(x), f₂(x) - непрерывные функции в интервале [a,b] и f₁(x) ≤ f₂(x), то, записывая двойной интеграл в виде повторного, получаем

В другом случае, когда область D(x,y) относится к типу II (является элементарной относительно оси Ox) и ограничена линиями

где φ₁(y), φ₂(y) - непрерывные на отрезке [c,d] функции, причем φ₁(y) ≤ φ₂(y), тройной интеграл представляется в виде

Формулы (1) и (2) называются формулами сведения тройного интеграла к повторному.  В частном случае, когда область интегрирования U представляет собой прямоугольный параллелепипед , тройной интеграл вычисляется по формуле

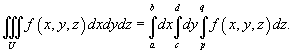
Если исходная область интегрирования U более сложная, чем рассмотренная выше, то ее нужно разбить на конечное число более простых областей, в которых уже можно вычислить тройные интегралы методом сведения к повторным. 

46-Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сфериферических координатах.

Пусть отображение устанавливает взаимно однозначное соответствие между областями и , причем функции - непрерывно дифференцируемые и

ни в одной точке .

Пусть - непрерывная на функция. Тогда 

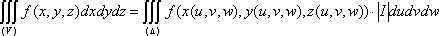
Как и для двойного интеграла (см. 1.4. Замена переменных в двойном интеграле), теорема остается верна в случае нарушения ее условий на множестве нулевого объема.

47-Приложения тройного интеграла(объем тела, масса, статистические моменты, координаты центра тяжести, момент инерции)

Масса и статические моменты тела

Пусть тело занимает объем U и его объемная плотность в точке M(x,y,z) задана функцией ρ(x,y,z). Тогда масса тела m вычисляется с помощью тройного интеграла:

Статические моменты тела относительно координатных плоскостей Oxy, Oxz, Oyz выражаются формулами

Координаты центра тяжести тела вычисляются по формулам:

Если тело является однородным с плотностью ρ(x,y,z) = 1 для точек M(x,y,z) в области U, то центр тяжести тела зависит только от геометрии тела и называется центроидом. 

Моменты инерции тела

Моменты инерции тела относительно координатных плоскостей Oxy, Oxz, Oyz определяются выражениями

а моменты инерции тела относительно координатных осей Ox, Oy, Oz вычисляются по формулам

Как видно, справедливы соотношения

Моментом инерции тела относительно начала координат называется интеграл

Момент инерции относительно начала координат можно выразить через моменты инерции относительно координатных плоскостей:

Тензор инерции

Используя рассмотренные выше 6 чисел I_x, I_y, I_z, I_xy, I_xz, I_yz, можно составить так называемую матрицу инерции или тензор инерции тела:

Данный тензор является симметричным, и, следовательно, его можно привести к диагональному виду при определенном выборе осей Ox', Oy', Oz'. Значения диагональных элементов (после приведения тензора к диагональному виду) называются главными моментами инерции, а указанные направления − собственными векторами или главными осями инерции.  Если тело вращается вокруг оси, не совпадаюшей с главной осью инерции, то оно будет испытывать вибрации при высоких скоростях вращения. Поэтому, при конструировании таких устройств необходимо, чтобы ось вращения совпадала с одной из главных осей инерции. Например, при замене шин автомобиля проводится их балансировка: небольшие грузики добавляются к колесам, чтобы обеспечить совпадение оси вращения с главной осью инерции и исключить вибрации. 

Гравитационный потенциал и сила тяготения

Ньютоновым потенциалом тела в точке P(x,y,z) называется интеграл

где ρ(ξ,η,ζ) − плотность тела, и .  Интегрирование выполняется по всему объему тела. Зная потенциал, можно вычислить силу притяжения материальной точки массы m и заданного распределенного тела с плотностью ρ(ξ,η,ζ) по формуле

где G − гравитационная постоянная.