Доказательство формулы Ньютона-Лейбница

Чтобы доказать данную теорему введем вспомогательную функцию

Здесь мы поступили следующим образом Мы заменили верхний предел интегрирования на переменную x; Вместо х под знаком интеграла написали переменную t. Это возможно поскольку значение определенного интеграла не зависит от обозначения переменной интегрирования:

Функция G(x) представляет собой Интеграл с переменным верхним пределом интегрирования! Теперь к этой функции мы применим определение производной как предел разностного отношения. 

Преобразуем числитель данной формулы, используя Свойства определенного интеграла 

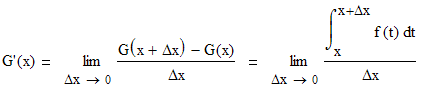
Теперь нам понадобится Теорема о среднем значении для определенного интеграла 

Здесь точка лежит между x и поэтому, когда стремится к нулю, стремится к х!

Это означает, что интеграл с переменным верхним пределом является первообразной для функции f(x). Любая другая первообразная подынтегральной функции отличается от данной первообразной на постоянную:

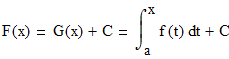
отсюда

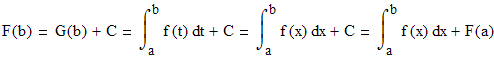
И формула Ньютона-Лейбница доказана

17-основные свойства определенного интеграла

I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. , где х, t – любые буквы.

II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

V. Постоянный множитель можно выносить за знак определенного интеграла.

VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

18-Интегрирование определенного интеграла:подстановкой,по частям

Положив в , что, т.е. переменнаяявляется функцией от, тогда

получим выражения для и. Теперь подставим полученные выражения в интеграл, следовательно:

где --произвольная постоянная и функция-- обратная функция к. Такое преобразование интеграла называетсяинтегрированием подстановкой (замена переменных).

Замечание. Последнее действие в предыдущем равенстве является обязательным, т.к. интеграл зависит от переменной , следовательно, ответ должен быть функцией от. Это операция называется -обратная замена переменных.

Общая замена переменных выглядит следующим образом:

тогда

и, используя эти равенства, добиваемся, чтобы в исходном интеграле, зависящим от , не было вхождения, т.е.

Здесь следуя предыдущему замечанию необходимо сделать обратную замену переменных. Отметим, что если изначально, например, интегрировали по , то ответ не должен содержать других переменных кроме.

Например.

Вычислить интеграл:

Решение.

Сделаем замену переменных и найдемдифференциалот обеих частей, тогда

Подставляя все в исходный интеграл, получим:

где . Здесь заключительное действие - этообратная замена переменных.

В данном случае с помощью замены в интеграле удалось свести интеграл к табличному, затем была произведена обратная замена переменных и получен ответ.

Самой простой подстановкой (заменой переменных) является линейная замена, частный случай общей замены переменных.

Линейная подстановка (линейная замена) применяется для интегралов вида

Положив

получаем:

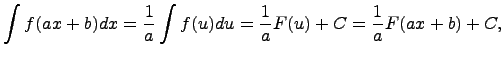
здесь -первообразная для.

Способ непосредственного интегрирования состоит в том, чтобы, применяя только свойства интегралов, свести его к табличному интегралу.

Например.

Вычислить интеграл:

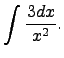
Решение.

Применяя свойства интеграла(линейность), т.е., сводим ктабличному интегралу, получаем, что

где .

по частям