Объёмы тел вращения.

13.4.1. Вычисление объёма тела по площадям поперечных сечений. Пусть тело V расположено в пространстве между плоскостями x = a и x = b, и для известна площадь его поперечного сечения S = S(x). Требуется определить объём этого тела.   Рассечём это тело плоскостями x = x₀ = a, x = x₁, x = x ₂, …, x = x_i-1, x = x_i, …, x = x _n-1, x = x_n = b на n слоёв (a = x₀< x₁ < < x₂< …< x_n-1 < x_n = b), на каждом из отрезков [x_i-1, x_i] возьмём произвольную точку ; будем считать, что объём слоя, заключенного между плоскостями x = x_i-1 и x = x_i приближённо равен объёму цилиндрика с площадью основания и высотой : . Сумма объёмов - объём ступенчатой фигуры - при стремится к искомому объёму V, поэтому .  13.4.2. Объём тела, получающегося при вращении кривой вокруг координатной оси. Если объём V получается в результате вращения кривой y = f(x), , вокруг оси Ox, то, очевидно, , поэтому .  Пример: найти объём эллипсоида, получающегося при вращении эллипса вокруг оси Ox.  Решение: эту задачу проще решить, если применить параметрические уравнения эллипса: . Верхняя дуга эллипса получается при изменении t от 0 до , при этом точке крайней левой точке эллипса соответствует значение параметра t₀ , равное , крайней правой точке соответствует значение t_k = 0. Формула для кривой, заданной параметрически,примет вид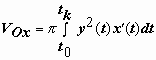, поэтому 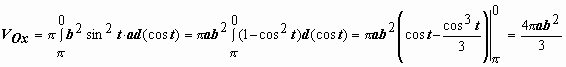.  Если требуется найти объём тела, которой получается при вращении плоской фигуры ABCD вокруг оси Oy, рассуждаем по другому. Разбиваем тело на полые цилиндры радиуса x, толщины , высоты f(x). Объём этого цилиндра равен произведению длины окружности на толщину и высоты f(x); суммируя эти объёмы и переходя к пределу при , получим .  13.4.3. Объём тела, получающийся при вращении сектора, ограниченного кривой и двумя полярными радиусами и , вокруг полярной оси находится по формуле .  Пример: найти объём тора, полученного вращением окружности вокруг полярной оси.  Решение: 

Площадь поверхности вращения.

Площадь поверхности вращения, образующейся при вращении вокруг оси Ox дифференцируемой кривой, определяется по формулам (в зависимости от способа задания кривой) 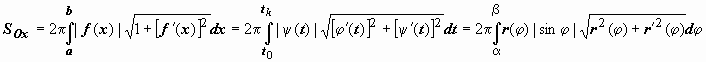(- длина окружности кольца,- его ширина).Пример: найти площадь тора, образующегося при вращении окружностивокруг осиOx.  Решение:.

24-Механические приложения определенного интеграла работа силы путь, пройденный телом, вычисление статических моментов и координат центра тяжести плоской фигуры.

Механические приложения определенного интеграла

Работа переменной силы

Пусть материальная точка М перемещается вдоль оси Ох под действием переменной силы F = F(x), направленной параллельно этой оси. Работа, произведенная силой при перемещении точки М из положения х = а в положение х = b (a < b), находится по формуле (см. п. 36).

Пример 41.10 Какую работу нужно затратить, чтобы растянуть пружину на 0,05 м, если сила 100 Н растягивает пружину на 0,01 м?

Решение: По закону Гука упругая сила, растягивающая пружину, пропорциональна этому растяжению х, т. е. F = kх, где k — коэффициент пропорциональности. Согласно условию задачи, сила F = 100 Н растягивает пружину на х = 0,01 м; следовательно, 100 = k*0,01, откуда k = 10000; следовательно,F = 10000х.

Искомая работа на основании формулы (41.10) равна

Пример 41.11. Найти работу, которую необходимо затратить, чтобы выкачать через край жидкость из вертикального цилиндрического резервуара высоты Н м и радиусом основания R м.

Решение: Работа, затрачиваемая на поднятие тела весом р на высоту h, равна р•h. Но различные слои жидкости в резервуаре находятся на различных глубинах и высота поднятия (до края резервуара) различных слоев не одинакова.

Для решения поставленной задачи применим схему II (метод дифференциала). Введем систему координат так, как указано на рисунке 193.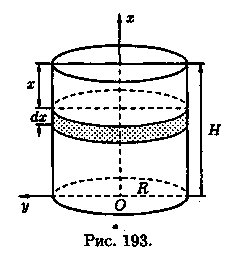

1. Работа, затрачиваемая на выкачивание из резервуара слоя жидкости толщиной x (0 !!!< x !!!< H), есть функция от х, т.е. А = А(х), где 0≤x≤H (А(0)=0, А(Н)=А₀).

2. Находим главную часть приращения ΔА при изменении х на величину Δх = dx, т. е. находим дифференциал dA функции А(х).

Ввиду малости dx считаем, что «элементарный» слой жидкости находится на одной глубине х (от края резервуара) (см. рис. 193). Тогда dA = dp*x, где dp — вес  этого слоя; он равен g *gdv, где g — ускорение свободного падения, g — плотность жидкости, dv — объем «элементарного» слоя жидкости (на рисунке он выделен), т. е. dp = ggdv. Объем указанного слоя жидкости, очевидно, равен πR² dx, где dx — высота цилиндра (слоя), πR² — площадь его основания, т. е. dv=πR² dx.

Таким образом, dp=ggπR² dx и dA = ggπR²dx*x.

3) Интегрируя полученное равенство в пределах от х = 0 до х = Н, находим

Путь, пройденный телом

Пусть материальная точка перемещается по прямой с переменной скоростью v=v(t). Найдем путь S, пройденный ею за промежуток времени от t₁ до t₂.

Решение: Из физического смысла производной известно, что при движении точки в одном направлении «скорость прямолинейного движения равна производной от пути по времени», т. е .. Отсюда следует, что dS = v(t)dt. Интегрируя полученное равенство в пределах от t₁ до t₂, получаем 

 

Отметим, что эту же формулу можно получить, пользуясь схемой I или II применения определенного интеграла.

Пример 41.12. Найти путь, пройденный телом за 4 секунды от начала движения, если скорость тела v(t) = 10t + 2 (м/с).

Решение: Если v(t)=10t+2 (м/с), то путь, пройденный телом от начала движения (t=0) до конца 4-й секунды, равен

Давление жидкости на вертикальную пластинку

По закону Паскаля давление жидкости на горизонтальную пластину равно весу столба этой жидкости, имеющего основанием пластинку, а высотой — глубину ее погружения от свободной поверхности жидкости, т. е. Р = g*g*S*h, где g — ускорение свободного падения,  g— плотность жидкости, S - площадь пластинки, h - глубина ее погружения.

По этой формуле нельзя искать давление жидкости на вертикально погруженную пластинку, так как ее разные точки лежат на разных глубинах.

Пусть в жидкость погружена вертикально пластина, ограниченная линиями х = а, х = b, у₁ = f₁(x) и у₂=ƒ₂(х); система координат выбрана так, как указано на рисунке 194. Для нахождения давления Р жидкости на эту пластину применим схему II (метод дифференциала).

1. Пусть часть искомой величины Р есть функция от х: р=р(х), т. е. р=р(х) — давление на часть пластины, соответствующее отрезку [а; х] значений переменной х, где х є [а; b] (р(а)=0,р(b) = Р).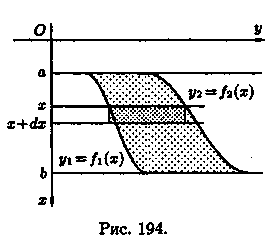

2. Дадим аргументу х приращение Δх = dx. Функция р(х) получит приращение Δр (на рисунке — полоска-слой толщины dx). Найдем дифференциал dp этой функции. Ввиду малости dx будем приближенно считать полоску прямоугольником, все точки которого находятся на одной  глубине х, т. е. пластинка эта — горизонтальная.

Тогда по закону Паскаля 

3. Интегрируя полученное равенство в пределах от х = а до х = В, получим

 

Пример 41.13. Определить величину давления воды на полукруг, вертикально погруженный в жидкость, если его радиус R, а центр О находится на свободной поверхности воды (см. рис. 195).

Решение: Воспользуемся полученной формулой для нахождения давления жидкости на вертикальную пластинку. В данном случае пластинка ограничена линиями х = 0, х=R. Поэтому

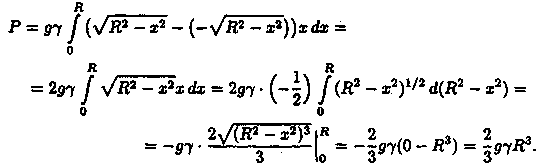
Вычисление статических моментов и координат центра тяжести плоской кривой

Пусть на плоскости Оху задана система материальных точек M₁ (x₁; y₁), М₂(х₂; у₂),..., М_n(х_n; у_n) соответственно с массами m₁, m₂,... ...,m_n.

Статическим моментом S_x системы материальных точек относительно оси Ох называется сумма произведений масс этих точек на их ординаты (т. е. на расстояния этих точек от оси Ох):

Аналогично определяется статический момент S_y этой системы относительно оси 

Если массы распределены непрерывным образом вдоль некоторой кривой, то для выражения статического момента понадобится интегрирование.

Пусть у = ƒ(х) (a≤x≤b) — это уравнение материальной кривой АВ. Будем считать ее однородной с постоянной линейной плотностью g (g = const).

Для произвольного х є [а; b] на кривой АВ найдется точка с координатами (х;у). Выделим на кривой элементарный участок длины dl, содержащий точку (х;у). Тогда масса этого участка равна g dl. Примем этот участок dl приближенно за точку, отстоящую от оси Ох на расстоянии у. Тогда дифференциал статического момента dS_x («элементарный момент») будет равен gdly, т. е. dS_x = gdlу (см. рис. 196).

Отсюда следует, что статический момент S_x кривой АВ относительно оси Ох равен

Аналогично находим S_y:

 Статические моменты S_x и S_y кривой позволяют легко установить положение ее центра тяжести (центра масс).

Центром тяжести материальной плоской кривой у = ƒ(х), х Î [a;b] называется точка плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу m заданной кривой, то статический момент этой точки относительно любой координатной оси будет равен статическому моменту всей кривой у = ƒ (х) относительно той же оси. Обозначим через С(х_с;у_с) центр тяжести кривой АВ.

Из определения центра тяжести следуют равенства  Отсюда или

Пример 41.14. Найти центр тяжести однородной дуги окружности x²+y²=R², расположенной в первой координатной четверти (см. рис. 197).

Решение: Очевидно, длина указанной дуги окружности равна πR/2, т. е. l=πR/2. Найдем статический момент ее относительно оси Ох. Так как уравнение дуги есть 

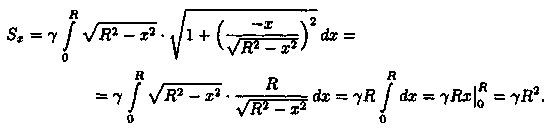
Стало быть,

Так как данная дуга симметричнаотносительно биссектрисы первого координатного угла, то х_с=у_с=2R/π. Итак, центр тяжести имеет координаты

 

Вычисление статических моментов и координат центра тяжести плоской фигуры

Пусть дана материальная плоская фигура (пластинка), ограниченная кривой у = ƒ(х)  0 и прямыми у = 0, х = a, x = b (см. рис. 198).

Будем считать, что поверхностная плотность пластинки постоянна (g = const). Тогда масса «всей пластинки равна g * S, т. еВыделим элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и будем приближенно считать его прямоугольником.

Тогда масса его равна gydx. Центр тяжести С пря моугольника лежит на пересечении диагоналей прямоугольника. Эта точка С отстоит от оси Ох на 1/2*у, а от оси Оу на х (приближенно; точнее на расстоянии х+¹/₂∆х). Тогда для элементарных статических моментов относительно осей Ох и Оу выполнены соотношения

Следовательно,

По аналогии с плоской кривой получаем, обозначив координаты центра тяжести плоской фигуры (пластинки) через С(х_с; у_с), что m•х_с=S_y, m•у_с=S_x. Отсюда

или

Пример 41.15. Найдем координаты центра тяжести полукруга х²+у²≤R², у≥0 (g=const) (см. рис. 199).

Решение: Очевидно (ввиду симметрии фигуры относительно оси Оу), что х_с=0. Площадь полукруга равнаНаходим S_x:

Стало быть,

Итак, центр тяжести имеет координаты 

25-Функции нескольких переменных. Предел функции. Непрерывность функции двух переменных. Свойства функций, непрерывных в ограниченной замкнутой области