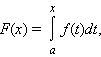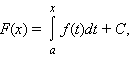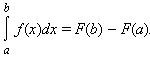1-Теоремы о дифференцируемых функциях Роля Коши Лангранжа(следствия)

Теорема Ролля.

Теорема: Если функция f(x) непрерывна на отрезке [a,b], дифференцируемая на отрезке (а,b) и на концах отрезка принимает одинаковое значение f(a)=f(b), то найдется хотя бы одна точка с(а,b), в которой производная f '(х) превращается в ноль, т.е. (f '(с)=0).

Доказательство: Пусть функция f(x) непрерывна на отрезке [a,b], тогда она достигает своего наибольшего значения М и наименьшего значения m на этом отрезке. Рассмотрим случаи:

1) Если М=m, то функция постоянна на [a,b] и следовательно f '(х)=0, (т.к. с'=0); 2) Если Mm, то функция достигает хотя бы одно из значений M или m во внутренних точках с на отрезке (a,b), т.к. f(а)=f(b).

Пусть например: 1) Функция принимает значение М в точке х=с(а,b), т.е. (Рис1) f(с)=M,тогда  х(а,b) выполняется соотношение f(c)>=f(x). Найдем производную f '(с) в точке: f '(с)=Lim[f(c+Δx)-f(c)]/Δx, т.к. f(c)>=f(x), то f(c+Δx)-f(c)<=0

• Если Δх>0(т.е. Δх0 справа от точки х=с), то [f(c+Δx)-f(c)]/Δx<=0, поэтому f '(с)<=0

• Если Δх<0, то [f(c+Δx)-f(c)]/Δx>=0, то f '(с)>=0. Таким образом, получим, что f '(c)<=0 и f '(с)>=0| f '(с)=0

2. Если f(с)=m, доказательство аналогично.

Примечание: Геометрически Теорема Ролля означает, что на графике функции y=f(x) найдется точка в которой касательная к графику параллельна оси ох (см. Рис1 и Рис2), (на Рис3 таких точек 2-е).

Теорема Коши

Если y=f(x) и φ(х) непрерывны на отрезке [a;b] и дифференцируемы на (a;b), причем , то найдется хотя бы одна точкатакая, что:

ДОКАЗАТЕЛЬСТВО:

φ (a)≠φ(b) по теореме Ролля, следовательно:

φ(b)- φ (a) ≠0

Рассмотрим вспомогательную функцию

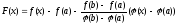
Эта функция удовлетворяет всем условиям т. Ролля: она непрерывна на [a;b], дифференцируема на (a;b), наконцах интервала f(a)=f(b)=0.

На основании т. Ролля найдется точка 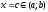, такая, что

Следовательно:

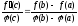что и требовалось доказать.

Теорема Лагранжа, ее геометрический смысл.

Если f(x) непрерывна на [a;b], дифференцируема на (a;b), то найдется хотя бы одна точка 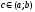, такая, чтоf(b)-f(a)=f ^I(c)(b-a)

ДОКАЗАТЕЛЬСТВО:

Положим в т. Коши φ(x)=x

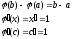Подставим эти значения в формулу:

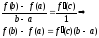Что и требовалось доказать.

Геометрический смысл т. Лагранжа:

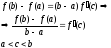
Отношение f(b)-f(a) / b-a есть угловой коэффициент секущей АВ, а величина f ^I(c) – угловой коэффициент касательной к кривой в точке x=c, следовательно геометрический смысл т. Лагранжа заключается в следующем: на графике y=f(x) найдется точка C(c;f(c)) в которой касательная к графику функции параллельна секущей АВ.

СЛЕДСТВИЕ:

Если, производная функции yⁱ=0 на некотором промежутке, то ф-я постоянна на этом промежутке.

Если две ф-ии имеют равные производные на некотором промежутке, то они отличны друг друга на постоянное слагаемое.

2-Правила Лопиталя

Правило Лопиталя для раскрытия неопределенностей

Если

То f(x) и φ(x) в некоторой окрестности содержат точку x=x₀ удовлетворяющую всем условиям т. Коши.

Предел отношения функций равен пределу отношения их производных.

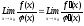
при условии, что предел правой части равенства существует.

Правило Лопиталя применимо и в том случае когда:

• Аргумент x стремится к бесконечности

• Если отношение производных f ^I и φⁱ при x стрем. к беск. Снова приводит к неопределенности вида 0/0 или ∞/∞.

При выполнении требуемых условий правило Лопиталя можно использовать повторно.

4-Необходимое и достаточное условия возрастания(убывания)функции

Экстремум функции. Необходимое и достаточное условие экстремума.

Точка x₀ наз-ся точкой max, если при любом х из некоторой δ-окрестности если выполняется неравенство: f(x) < f((x₀) при x≠x₀.

Точка x₀ наз-ся точкой min, если при любом х из некоторой δ-окрестности точки x₀ выполняется неравенство: f(x) > f((x₀) при x≠x₀.

Максимум(минимум) функции наз-ся экстремумом поскольку понятие экстремума связано с определением окрестности точки и Области Определения Функции то функция может иметь экстремум только во внутренних точках ОДЗ. Очевидно также, что функция может иметь несколько точек экстремума.

Необходимое условие экстремума:

Если функция f(x) имеет в точке х₀ экстремум и дифференцируема в этой точке, то f ^I(x₀)=0

Достаточное условие экстремума:

Непрерывная функция f(x) дифференцируема в δ-окрестности. Если при переходе через x­₀ (слева направо) производная f ^I меняет знак с + на – , то x₀ –есть точка max, если с – на +, то x₀ – точка min.

Исследовать функцию на экстремум это значит:

• Найти критические точки функции y=f(x) (для этого находится y^I и решается уравнение y^I=0)

• Исследовать знак производной f ^I слева и справа от каждой из выбранных критических точек.

В соответствии с достаточным условием экстремума выписать точки экстремума (если они есть) и вычислить значения функции в них.

6-Наибольшее и наименьшее значение функции на отрезке

Если y=f(x) непрерывная ф-я на [a:b], то на этом отрезке она по крайней мере 1 раз достигает наибольшего значения М и наименьшего значения m. Этих значений ф-я достигает либо в критических точках, либо на концах отрезка [a;b], поэтому чтобы найти наиб. и наим. значение ф-ии y=f(x) на заданном отрезке [a;b], где она непрерывна надо:

• Найти все критические точки принадлежащие (a;b) и вычислить значения ф-ии в этих точках (не исследуя их на экстремум)

• Вычислить значения ф-ии на концах [a;b], т.е. f(a) и f(b).

• Сравнить полученные результаты в пунктах 1 и 2, наиб. из них будет наиб. а наименьшее – наименьшим значением функции н отрезке [a;b]

Нахождение наиб. и наим. значений ф-ий широко используется при решении многих практических задач в математике, физике, экономике и т. п. и др.

ПРИМЕР:

y=2x³-3x²-12x+1 на [-2;5/2]

y^I=6x²-6x-12

y^I=0

6x²-6x-12=0 |:6

x²-x-2=0

x₁=-1 и x₂=2 – критические точки

y(-1)= 8 – наибольшее.

y(2)=-19 –наименьшее.

y(-2)=-3

y(5/2)=-16.5

7-Выпуклость графика функции. Точки перегиба.

Кривая y=f(x) называется выпуклой вверх (выпуклой) на интервале (a;b), если при a<x<b дуга располагается ниже касательной проведенной в любой точке (a;b).

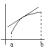
Кривая y=f(x) называется выпуклой вниз (вогнутой) на (a;b), если при a<x<b, дуга располагается выше касательной проведенной в любой точке (a;b).

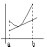
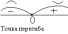
Точки отделяющие выпуклую вверх часть кривой от выпуклой вниз (или наоборот) называются точками перегиба, в точках перегиба касательная пересекает кривую.

Если ф-я y=f(x) во всех точках (a;b) имеет отрицательную вторую производную т.е. f ^II <0, то график ф-ии на этом интервале выпуклый вверх. Если f ^II >0, то он выпуклый вниз.

Достаточное условие существования точек перегиба.

Если f ^II(x) при переходе через x₀ в которой она равна 0 или не существует, меняет знак то точка графика с абсциссой x₀ есть точка перегиба.

ПРИМЕР:

y=x⁵-x+5

y^I=5x ⁴-1

y^II=20x³

20x³=0

x=0

График выпуклый вверх в интервале (-;0), график вогнутый на (0; +), (0;5) – точка перегиба.

8-Асимптоты графика функции.

Прямая l наз-ся асимптотой кривой y=f(x), если при удалении точки М(х;у) по кривой в бесконечность расстояние от точки М(х;у) стремится к 0.

Если асимптота параллельна Oy , то она называется вертикальной.

Если асимптота образует с O_x угол не равный 90⁰, то она наз-ся наклонной.

Lim f(x)=

xa

x=a –есть уравнение вертикальной асимптоты.

Для отыскания вертикальной асимптоты нужно найти х вблизи которого функция f(x) возрастает по модулю. Обычно это точки разрыва второго рода. Уравнение наклонной асимптоты будем искать в виде y=kx+b, где

k=Lim f(x)/x

x

b=Lim (f(x)-k(x))

x

Если хотя бы один из этих пределов не существует, то кривая асимптоты не имеет. Если k=0, b имеет конечное значение, то асимптота наз-ся горизонтальной.

9-Формула Тейлора для произвольной функции

Рассмотрим функцию у=ƒ(х). Формула Тейлора позволяет, при определенных условиях, приближенно представить функцию ƒ(х) в виде многочлена и дать оценку погрешности этого приближения.

Теорема 26.1. Если функция ƒ(х) определена в некоторой окрестности точки х₀ и имеет в ней производные до (n+1)-го порядка включительно, то для любого х из этой окрестности найдется точка сє(х₀;х) такая, что справедлива формула

Формула (26.3) называется формулой Тейлора для функции ƒ(х). Эту формулу можно записать в виде ƒ(х)=Р_n(х)+R_n(x), где

называется многочленом Тейлора, а

называется остаточным членом формулы Тейлора, записанным в форме Лагранжа. R_n(х) есть погрешность приближенного равенства ƒ(х)≈Р_n(х). Таким образом, формула Тейлора дает возможность заменить функцию у=ƒ(х) многочленом у=Р_n(х) с соответствующей степенью точности, равной значению остаточного члена R_n(x).

При х₀=0 получаем частный случай формулы Тейлора — формулу Маклорена:

где с находится между 0 и х (с=θx, 0<θ<1).

При n=0 формула Тейлора (26.3) имеет вид ƒ(х)=ƒ(х₀)+ƒ'(с)(х-х₀) или ƒ(х)-ƒ(х₀)=ƒ'(с)(х-x₀), т. е. совпадает с формулой Лагранжа конечных приращений. Рассмотренная ранее формула для приближенных вычислений ƒ(х)≈ƒ(х₀)+ƒ'(х₀)(х-х₀) (см. «дифференциал функции») является частным случаем более точной формулы

10-Комплексные числа в алгебраической форме и действия над ними.

Необходимость введения комплексных чисел возникла при решении задач, сводящихся к решению уравнения вида x² = a; a<0.

В процессе решения задач такого рода было введено новое число i, обладающее свойствами i² = -1.

Примем без доказательств, что можно ввести так называемые комплексные числа, такие что присоединив их к уже известным нам действительным числам, получим множество чисел, над которыми можно по обычным правилам выполнять арифметические действия и кроме того среди новых чисел будет присутствовать число i, обладающее вышеуказанными свойствами.

Определение: числа вида z = a + bi, где a и b – два действительных числа, называют комплексными. Число a называют действительной частью, bi – мнимой частью, b – коэффициент при мнимой части, i – мнимая единица.

Два комплексных числа

z₁ = a₁ + b₁i

z₂ = a₂ + b₂i

считаются равными т. т. т. когда равны их действительные части и коэффициенты при мнимой единице, т. е. a₁=a₂; b₁=b₂.

Если a=0, то к/ч z = a + bi обращается в чисто мнимое число z = bi.

Если b=0, то к/ч z = a + bi становится действительным числом равным a.

Т. о. все действительные числа, а также чисто мнимые числа являются подмножеством множества к/ч C.

Способ записи к/ч в виде z = a + bi называется алгебраической формой к/числа.

Примечание:

1. С помощью мнимой единицы может быть выражен квадратный корень из отрицательного числа:-4 = 4-1 = 2i

2. Введение к/ч делает возможным решение квадратных уравнений с отрицательным дискриминантом.

Определение: сопряжённый к/числу z = a + bi называется числоz = a – bi, т. е. два сопряжённых числа отличаются друг от друга только знаками перед мнимой частью.

Действия над к/ч-ми в алгебраической форме.

Определение: суммой двух ч/чисел z₁ = a + bi и z₂ = c + di называется к/число, действительная часть которого равна сумме действительных частей слагаемых, а мнимая – сумме мнимых частей: z₁+z₂ = a+c+(b+d)i.

Определение: разностью двух к/чисел z₁ и z₂ называется к/ч, действительная часть которого равна разности действительных частей z₁ и z₂, а мнимая – разности их мнимых частей: z₁-z₂ = a-c+(b-d)i.

Определение: произведение двух к/чисел z₁ и z₂ называется к/ч полученное по правилу умножения обычных многочленов, в полученном результате i² заменяется на (-1) и отделяется действительная часть от мнимой: z₁*z₂ = (a+bi)(c+di) = ac+adi+bdi²+bci = ac+adi+bci-bd = (ac-bd)+(ad+bc)i .

Определение: Частное двух к/ч z₁ и z₂ называется к/ч, полученное умножением числителя и знаменателя дроби на число сопряжённое знаменателю: (a+bi)/(c+di) =

(a+bi)(c-di)/(c²+di²) = (ac+bd+(bc-ad)i)/(c²+d²)

Степени мнимой единицы.

Пользуясь равенством i²=(-1) легко определить любую целую положительную степень мнимой единицы:

i¹ = i i⁵ = i

i² = (-1) i⁶ = (-1)

i³ = i²i = (-i) i⁷ = (-i)

i⁴ = 1 i⁸ = 1

и т. д.…

Легко увидеть, что значение степени iⁿ, где n- целое положительное число, периодически повторяются при увеличении показателя на 4, поэтому, чтобы возвести число i в целую положительную степень надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.

i⁴ⁿ⁺¹ = i i⁴ⁿ⁺³ = -i

i⁴ⁿ⁺² = -1 i⁴ⁿ = 1

Геометрическая интерпретация к/ч в алгебраической форме.

К/число z = a+bi изображается на плоскости Oxy точкой M(a;b) или радиусом вектором OM проекции которого на оси Ox и Oy соответственно равны a и b.

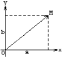
Плоскость Oxy в этом случае называется условно комплексной плоскостью.

К/ч (a;0) отождествляется с действительным числом a. На к/плоскости действительные числа изображаются точками на оси Ox, которая называется действительной осью.

К/ч (a;b); b0 называется мнимым, а при a=0 – чисто мнимым.

Чисто мнимые числа на к/плоскости изображаются точками на оси Oy, которая называется мнимой осью.

Если z иz сопряжённые числа, то числоz изображается на к/плоскости точкой, симметричной точке z относительно оси Ox.

Замечание: понятия «больше» или «меньше» для к/чисел не определяются. Записи z>0; i>2; 1+i>2 и т. п. Лишены всякого смысла.

11- Неопределенный Интеграл. Первообразная функции. Свойства неопределенного интеграла.

Первообразная и неопределенный интеграл Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции

F'(x) = f(x).

Обозначение

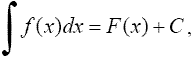
где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением.

Свойства неопределенного интеграла 1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

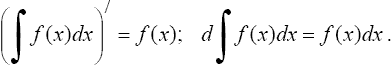
2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

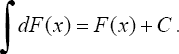
3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то

4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

12-Таблица основных интегралов

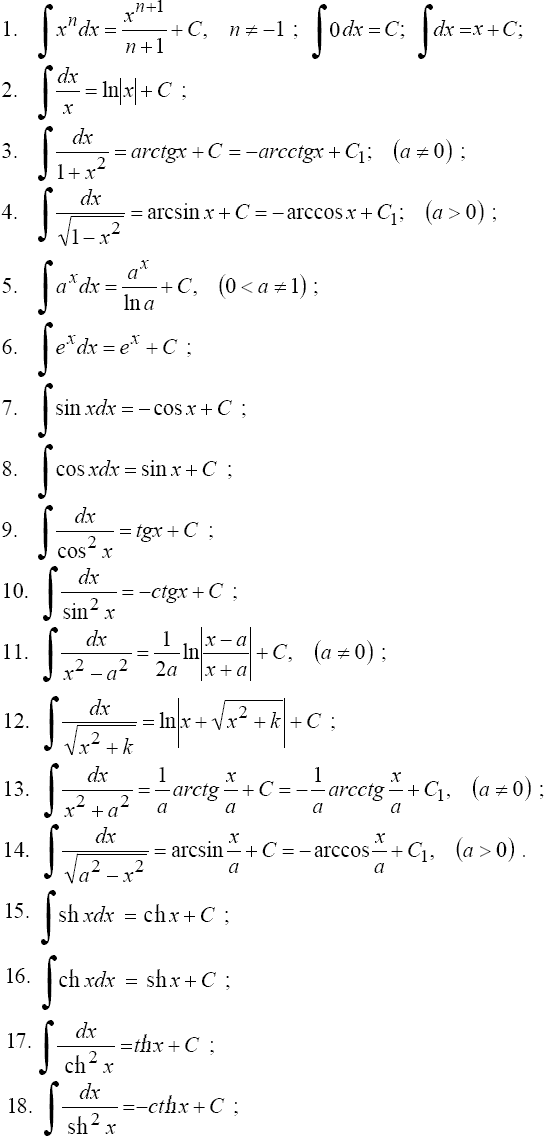
13-Основные методы интегрирования

I. Метод непосредственного интегрирования

Задача нахождения неопределенных интегралов от многих функций решается методом сведения их к одному из табличных интегралов.

Пример 1.

∫(1-√x)²dx=∫(1-2√x+x)dx=∫dx-∫2√xdx+∫xdx=∫dx-2∫xdx+∫xdx=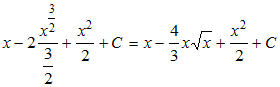

Пример 2.

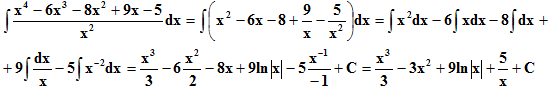
Пример 3. ∫sin²xdx

Так как sin²x=(1-cos2x), то  ∫sin²xdx=(1-cos2x)dx=∫dx-∫cos2xd(2x)=x-sin2x+C

Пример 4. ∫sinxcos3xdx

Так как sinxcos3x=(sin4x-sin2x), то имеем  ∫sinxcos3xdx=∫(sin4x-sin2x)dx=∫sin4xd(4x)-∫sin2xd(2x)=-cos4x+cos2x+C

Пример 5. Найти неопределенный интеграл: ∫cos(7x-3)dx

∫cos(7x-3)=∫cos(7x-3)d(7x-3)=sin(7x-3)+C

Пример 6. 

II. Метод подстановки (интегрирование заменой переменной)

Если функция x=φ(t) имеет непрерывную производную, то в данном неопределенном интеграле ∫f(x)dx всегда можно перейти к новой переменной t по формуле

∫f(x)dx=∫f(φ(t))φ'(t)dt

Затем найти интеграл из правой части и вернуться к исходной переменной. При этом, интеграл стоящий в правой части данного равенства может оказаться проще интеграла, стоящего в левой части этого равенства, или даже табличным. Такой способ нахождения интеграла называется методом замены переменной.

Пример 7. ∫x√x-5dx

Чтобы избавиться от корня, полагаем √x-5=t. Отсюда x=t²+5 и, следовательно, dx=2tdt. Производя подстановку, последовательно имеем:

∫x√x-5dx=∫(t²+5)•2tdt=∫(2t⁴+10t²)dt=2∫t⁴dt+10∫t²dt=

Пример 8. 

Так как , то имеем

Пример 9. 

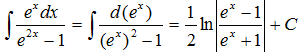
Пример 10. ∫e^-x3x²dx

Воспользуемся подстановкой -x³=t. Тогда имеем -3x²dx=dt и ∫e^-x3x²dx=∫e^t(-1/3)dt=-1/3e^t+C=-1/3e^-x3+C

Пример 11. 

Применим подстановку 1+sinx=t , тогда cosxdx=dt и 

III. Метод интегрирования по частям

Метод интегрирование по частям основан на следующей формуле:

∫udv=uv-∫vdu

где u(x),v(x) –непрерывно дифференцируемые функции. Формула называется формулой интегрирования по частям. Данная формула показывает, что интеграл ∫udv приводит к интегралу ∫vdu, который может оказаться более простым, чем исходный, или даже табличным.

Пример 12. Найти неопределенный интеграл ∫xe^-2xdx

Воспользуемся методом интегрирование по частям. Положим u=x, dv=e^-2xdx. Тогда du=dx, v=∫xe^-2xdx=-e^-2x+C  Следовательно по формуле имеем:  ∫xe^-2xdx=x(-e^-2x)-∫-^-2dx=-e^-2x-e^-2x+C

Пример 13. ∫(x²+2x)cos2xdx

u=x²+2x, du=(2x+2)dx, dv=cos2xdx, v=∫cos2xdx=sin2x

∫(x²+2x)cos2xdx=(x²+2x)sin2x-∫(x+1)sin2xdx

u=x+1, du=dx, dv=sin2xdx, v=-cos2x

(x²+2x)sin2x-∫(x+1)sin2xdx=(x²+2x)sin2x+(x+1)cos2x+sin2x+C

14-Определенный интеграл как предел интегральной суммы.Теорема Коши.

Пусть функция у=ƒ(х) определена на отрезке [а; b], а < b. Выполним следующие действия.

1. С помощью точек х₀=а, x_1, х_{2, ...,} х_n = В (х₀ <x₁ < ...< х_n) разобьем отрезок [а, b] на n частичных отрезков [х₀;х₁], [x₁; х₂],..., [х_n-1,х_n] (см. рис. 167).

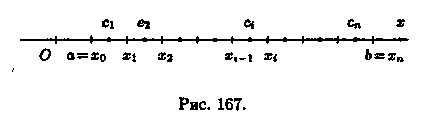
2. В каждом частичном отрезке [x_i-1;x_i], i = 1,2,...,n выберем произвольную точку с_i є [x_i-1; x_i] и вычислим значение функции в ней, т. е. величину ƒ(с_i)

3. Умножим найденное значение функции ƒ (с_i) на длину ∆x_i=x_i-x_i-1 соответствующего частичного отрезка: ƒ (с_i) • ∆х_i.

4. Составим сумму S_n всех таких произведений:

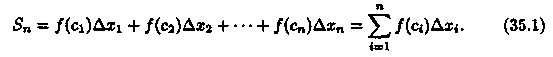
Сумма вида (35.1) называется интегральной суммой функции у = ƒ(х) на отрезке [а; b]. Обозначим через λ длину наибольшего частичного отрезка: λ = max ∆x_i(i = 1,2,..., n).

5. Найдем предел интегральной суммы (35.1), когда n → ∞ так, что λ→0.

Если при этом интегральная сумма S_n имеет предел I, который не зависит ни от способа разбиения отрезка [а; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = ƒ(х) на отрезке [а; b] и обозначается 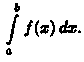Таким образом,

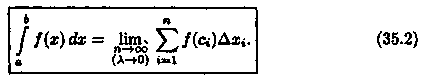
Числа а и b называются соответственна нижним и верхним пределами интегрирования, ƒ(х) — подынтегральной функцией, ƒ(х) dx — подынтегральным выражением, х — переменной интегрирования, отрезок [а; b] — областью (отрезком) интегрирования.

Функция у=ƒ(х), для которой на отрезке [а; b] существует определенный интеграл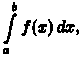называется интегрируемой на этом отрезке.

Сформулируем теперь теорему существования определенного интеграла.

Теорема 35.1 (Коши). Если функция у = ƒ(х) непрерывна на отрезке [а; b], то определенный интеграл

Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.

Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения (35.2).

1. Определенный интеграл не зависим от обозначения переменной интегрирования: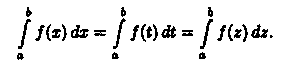

Это следует из того, что интегральная сумма (35.1), а следовательно, и ее предел (35.2) не зависят от того, какой буквой обозначается аргумент данной функции.

2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю: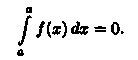

3. Для любого действительного числа с.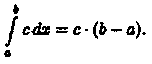

15-Геометрический и физический смысл определенного интеграла.

Площадь криволинейной трапеции

Пусть на отрезке [а; b] задана непрерывная функция у = ƒ(х) ≥ 0. Фигура, ограниченная сверху графиком функции у = ƒ(х), снизу — осью Ох, сбоку — прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции.

Для этого отрезок [а; b] точками а=х₀, х₁, ..., b=х_n (х₀<x₁<...<x_n) paзобьем на n частичных отрезков [х_о;х₁], [х₁;х₂],...,[х_n-1;х_n]. (см. рис. 168). В каждом частичном отрезке [x_i-1;x_i] (i=1,2,..., n) возьмем произвольную точку ci и вычислим значение функции в ней, т. е. ƒ(c_i).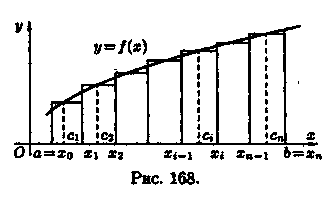

Умножим значением функции ƒ(c_i) на  длину ∆x_i=x_i-x_i-1 соответствующего частичного отрезка. Произведение ƒ(c_i) • ∆x_i равно площади прямоугольника с основанием ∆x_i и высотой ƒ(c_i). Сумма всех таких произведений

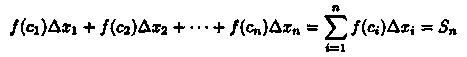
равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:

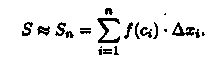
С уменьшением всех величин Δх_i точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры S_n, когда n неограниченно возрастает так, что λ = max∆x_i →0:

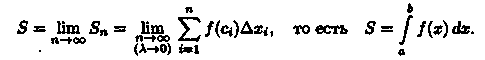
Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

В этом состоит геометрический смысл определенного интеграла.

Работа переменной силы

Пусть материальная точка М перемещается под действием силы F, направленной вдоль оси Ох и имеющей переменную величину F = F(x), где х — абсцисса движущейся точки М.

Найдем работу А силы F по перемещению точки М вдоль оси Ох из точки х = а в точку х = b (а < b). Для этого отрезок [а; b] точками а = х₀, х₁, ..., b = х_n (х₀ < x₁ < ... < х_n) разобьем на n частичных отрезков [х₀; x₁], [x₁; x₂],..., [x_n-1; x_n]. Сила, действующая на отрезке [x_i-1; x_i], меняется от точки к точке. Но если длина отрезка Δхi = х_i-x_i-1 достаточно мала, то сила F на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции F = F(x) в произвольно выбранной точке х = c_i Î [x_i-1; x_i]. Поэтому работа, совершенная этой силой на отрезке [x_i-1;x_i], равна произведению F(c_i)•Δх_i (Как работа постоянной силы F(c_i) на участке [x_i-1; x_i].)

Приближенное значение работы А силы F на всем отрезке [а; b] есть

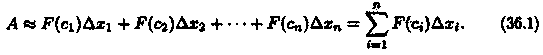
Это приближенное равенство тем точнее, чем меньше длина Δх_i Поэтому за точное значение работы А принимается предел суммы (36.1) при условии, что наибольшая длина λ частичных отрезков стремится к нулю:

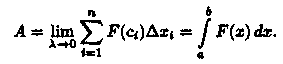
Итак, работа переменной силы F , величина которой есть непрерывная функция F = F(x), действующей на отрезке [а; b], равна определенному интегралу от величины F(x) силы, взятому по отрезку [а; b].

В этом состоит физический смысл определенного интеграла.

Аналогично можно показать, что путь S, пройденный точкой за промежуток времени от t=а до t=b, равен определенному интегралу от скорости v(t):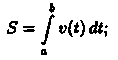

масса m неоднородного стержня на отрезке [a,b] равна определенному интегралу от плотности g(х):

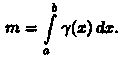
16-формула Ньютона-Лейбница

Формула Ньютона – Лейбница

Если функция f (x) интегрируема на [a; b], то для любого существует интеграл 

который называется интегралом с переменным верхним пределом.

Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке.

Если функция f интегрируема на [a; b] и непрерывна в то функция F (x) дифференцируема в  причем 

Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида 

где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.

 

Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:

Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда 

Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).

Пусть f (x) непрерывна на [a; b], g (t) имеет непрерывную производную на [α; β], Тогда если a = g (α), b = g (β), то справедлива формула замены переменной в определенном интеграле: 

Если функции u (x) и v (x) имеют на [a; b] непрерывные производные, то справедлива формула интегрирования по частям: